1
Given this function, 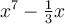 , what is the first
derivative?
, what is the first
derivative?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
2
Suppose a person starts at position 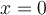 . Assume that
the person's next and final discreet choice on a decision tree is to either move to
. Assume that
the person's next and final discreet choice on a decision tree is to either move to 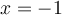 or
or 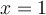 and the results of that choice are governed by the profit equation,
and the results of that choice are governed by the profit equation,
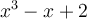 . What is the correct choice and associated
economic rationale?
. What is the correct choice and associated
economic rationale?
Choose one answer.
|
a. Move to -1 because |
||
|
b. Move to 1 because |
||
|
c. Move to 1 because |
||
| d. The person is indifferent between the two choices because the end result is the same. |
Question
3
Suppose a person starts at position 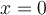 . Assume that
the person's next and final discreet choice on a decision tree is to either move to
. Assume that
the person's next and final discreet choice on a decision tree is to either move to 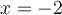 or
or 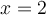 and the results of that choice are governed by the profit equation,
and the results of that choice are governed by the profit equation,
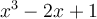 . What is the optimal result?
. What is the optimal result?
Choose one answer.
| a. Only lose -5 on this last choice. | ||
| b. Only lose -3 on this last choice. | ||
| c. Make 5 in profit. | ||
| d. Break even. |
Question
4
Suppose a firm's profit is given by this function, 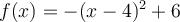 . The government imposes a lump sum profit tax of 5. For what values of
. The government imposes a lump sum profit tax of 5. For what values of 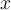 will profit be positive?
will profit be positive?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There are no values because the tax has made the firm unprofitable. |
Question
5
Suppose a firm has a production process governed by this function: 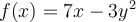 . What would be the marginal effect of using an additional unit of
. What would be the marginal effect of using an additional unit of
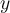 and holding
and holding 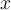 constant?
constant?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
6
Suppose a firm has a production process governed by this function: 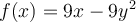 . What would be the marginal effect of using an additional unit of
. What would be the marginal effect of using an additional unit of
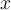 and holding
and holding 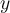 constant?
constant?
Choose one answer.
| a. 9 | ||
|
b. |
||
|
c. |
||
|
d. |
Question
7
Suppose you are given a profit function: 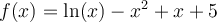 . What
tools would you use to solve for the value of a global maximum?
. What
tools would you use to solve for the value of a global maximum?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. Algebraic substitution |
Question
8
Suppose a firm's production choices were given by this multivariate expression: 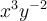 . What tools would you use to solve for marginal contribution to
production of
. What tools would you use to solve for marginal contribution to
production of 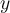 ?
?
Choose one answer.
|
a. The partial derivative of |
||
|
b. The partial derivative of |
||
|
c. The partial derivative of |
||
|
d. The partial derivative of |
Question
9
Suppose a government faced a series of discrete policy choices building a tax code. Earlier decisions would affect the options of later ones. What's the
best economic tool to use to evaluate the process?
Choose one answer.
| a. Dynamic optimization | ||
| b. Decision tree | ||
| c. Partial derivative | ||
| d. Second derivative, but only at the margin |
Question
10
Given this function, 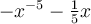 , what is the second
derivative?
, what is the second
derivative?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
11
Given this function, 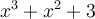 , what is a local minimum
value for
, what is a local minimum
value for 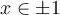 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
12
Given this function, 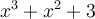 , what is the maximum value
for
, what is the maximum value
for 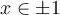 ?
?
Choose one answer.
| a. y = 0 | ||
| b. y = 3 | ||
| c. y = 5 | ||
|
d. |
Question
13
Given this function, 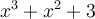 , what is the maximum value
for all values of
, what is the maximum value
for all values of 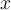 ?
?
Choose one answer.
| a. -4 | ||
| b. 0 | ||
| c. +4 | ||
|
d. |
Question
14
Given this function, 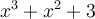 , what is the minimum value
for all values of
, what is the minimum value
for all values of 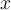 ?
?
Choose one answer.
| a. -4 | ||
| b. 0 | ||
| c. +4 | ||
|
d. |
Question
15
Given this function, 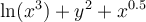 , what is the partial
derivative with respect to
, what is the partial
derivative with respect to 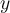 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
16
Given this function, 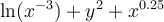 , what is the partial double
derivative with respect to
, what is the partial double
derivative with respect to 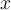 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
| c. 2 | ||
|
d. |
Question
17
Suppose a firm's profit is given by this function, 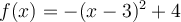 . For what values of
. For what values of 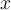 will profit be
maximized?
will profit be
maximized?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. Profits are maximized at all points. |
Question
18
Suppose that the relationship between economic growth 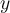 and population
and population 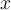 is given by the following
formula:
is given by the following
formula: 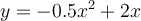 . What is the maximum sustainable yield?
. What is the maximum sustainable yield?
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. 2 | ||
| d. 4 |
Question
19
Suppose that the relationship between economic growth 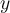 and population
and population 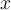 is given by the following
formula:
is given by the following
formula: 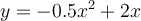 . What is the maximum possible size of
the entire population?
. What is the maximum possible size of
the entire population?
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. 2 | ||
| d. 4 |
Question
20
Suppose that the relationship between economic growth 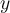 and population
and population 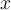 is given by the following
formula:
is given by the following
formula: 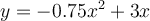 . What is the maximum sustainable yield?
. What is the maximum sustainable yield?
Choose one answer.
| a. 0 | ||
| b. 3 | ||
| c. 4.5 | ||
| d. 9 |
Question
21
Suppose that the relationship between economic growth 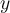 and population
and population 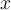 is given by the following
formula:
is given by the following
formula: 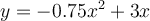 . What is the required initial
population to reach the maximum sustainable yield?
. What is the required initial
population to reach the maximum sustainable yield?
Choose one answer.
| a. 0 | ||
| b. 0.75 | ||
| c. 1 | ||
| d. 2 |
Question
22
Suppose that the relationship between economic growth 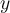 and carbon dioxide levels
and carbon dioxide levels 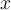 is given by the
following formula:
is given by the
following formula: 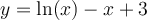 . What is the maximum
sustainable growth?
. What is the maximum
sustainable growth?
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. 1.5 | ||
| d. 2 |
Question
23
Suppose that the relationship between economic growth 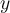 and carbon dioxide levels
and carbon dioxide levels 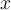 is given by the
following formula:
is given by the
following formula: 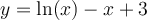 . To achieve the maximum
sustainable growth, what is the optimal choice for carbon dioxide levels?
. To achieve the maximum
sustainable growth, what is the optimal choice for carbon dioxide levels?
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. 1.5 | ||
| d. 2 |
Question
24
Suppose that the relationship between economic growth 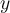 and carbon dioxide levels
and carbon dioxide levels 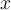 is given by the
following formula:
is given by the
following formula: 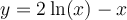 . How much growth is
attainable?
. How much growth is
attainable?
Choose one answer.
| a. If the country set carbon dioxide levels to zero, then growth would be zero. | ||
| b. If the country set carbon dioxide levels to 1, growth would be steady. | ||
| c. If the country set carbon dioxide levels to 2, growth would be positive but not sustainable. | ||
| d. Positive growth is not possible at any carbon dioxide level. |
Question
25
In univariate economic development models, which economic tool(s) can determine the maximum sustainable growth?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. Hamiltonian |
Question
26
In multivariate economic development models, which economic tool(s) can determine the contribution to growth of one variable, ceteris paribus?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. The identity matrix |
Question
27
What is the value of an annuity paying $7,000 at the end of every year for 5 years at a rate of 2 percent?
Choose one answer.
| a. $30,000 | ||
| b. $31,000 | ||
| c. $32,000 | ||
| d. $33,000 |
Question
28
You just won the Irish Sweepstakes and can either take a lump sum distribution today of €250,000 or a 20-year 5 percent annuity paying €20,000 at the end
of every year for 20 years. What is the best choice?
Choose one answer.
| a. The lump sum payment is a better deal, but by less than €1,000. | ||
| b. The lump sum payment is a better deal, but by more than €1,000. | ||
| c. The annuity is a better deal, but by less than €1,000. | ||
| d. The annuity is a better deal, but by more than €1,000. |
Question
29
Suppose the Federal Reserve Bank drives interest rates to less than zero. How much will an annuity paying $1,000 at the end of each year for three years at
an interest rate of
Choose one answer.
| a. More than $3,000 | ||
| b. $3,000 | ||
| c. Less than $3,000 | ||
|
d. Exactly $ |
Question
30
Which mathematical symbol is the best economic tool to calculate perpetual annuities?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
31
In calculating an annuity, what mathematical technique can be applied to account for default?
Choose one answer.
| a. Random number operator | ||
| b. Dynamic optimization | ||
| c. Expectations operator | ||
| d. Recursive optimization |
Question
32
Suppose two banks offer five-year annuities. Bank A offers a rate of 4 percent and Bank B offers 6 percent. Which statement is correct?
Choose one answer.
| a. The market could be pricing in a greater likelihood of a possible default by Bank B, ceteris paribus. | ||
| b. Bank A | ||
| c. Bank B may need to attract more capital than Bank A, ceteris paribus. | ||
| d. All of the above. |
Question
33
What is the value of an annuity paying $9,000 at the end of every year for nine years at a rate of 9 percent?
Choose one answer.
| a. $50,000 | ||
| b. $52,000 | ||
| c. $54,000 | ||
| d. $56,000 |
Question
34
What is the value of an annuity paying $2,000 at the end of every year for 10 years at a rate of 0 percent?
Choose one answer.
| a. $0 | ||
| b. $18,000 | ||
| c. $19,000 | ||
| d. $20,000 |
Question
35
The compound rate of interest on a savings account is 9 percent. Inflation is 7 percent. You deposit $25,000 and leave it in the account for 10 years. If
the bank credits this new account with a one-time $100 bonus, what will be the value in the account at the end of ten years?
Choose one answer.
| a. $57,777 | ||
| b. $58,821 | ||
| c. $59,121 | ||
| d. $59,421 |
Question
36
The compound rate of interest on a savings account is 4 percent. Inflation is 1 percent. You deposit $50,000 and leave it in the account for three years.
What will be the real purchasing power of the value in the account at the end of three years?
Choose one answer.
| a. $48,912 | ||
| b. $54,636 | ||
| c. $56,275 | ||
| d. $56,666 |
Question
37
The compound rate of interest on a savings account is 4 percent. Inflation is 2 percent. You deposit $10,000 and leave it in the account for two years.
What will be the real purchasing power of the value in the account at the end of two years?
Choose one answer.
| a. $9,924 | ||
| b. $10,204 | ||
| c. $10,404 | ||
| d. $10,824 |
Question
38
Suppose you bid at a government auction where the bids are sealed in envelopes with only one chance to bid. The winning bid gets the job and all others
receive nothing. You bid on a job at a price of $2 million, and you know that your cost is $1,800,000. If the probability that you'll win is 15 percent,
what is the expected value?
Choose one answer.
| a. $0 | ||
| b. $25,000 | ||
| c. $30,000 | ||
| d. 15% |
Question
39
Suppose you bid at a government auction where the bids are sealed in envelopes with only one chance to bid. The winning bid gets the job and all others
receive nothing. You bid on a job at a price of $100 million, and you know that your cost is $95 million. If the probability that you'll win is 10 percent,
what is the expected value?
Choose one answer.
| a. $0 | ||
| b. $500,000 | ||
| c. $1,000,000 | ||
| d. $5,000,000 |
Question
40
Suppose you consider bidding at a government auction where the bids are sealed in envelopes with only one chance to bid. The winning bid gets the job and
all others receive nothing. All bidders must pay a $25,000 bribe to participate. You intend to bid on a job at a price of $10 million, and you know that
your cost to complete the job is $8 million. If the probability that you'll win is 50 percent, what is the rational course of action?
Choose one answer.
| a. Raise your bid to $10,025,000. | ||
| b. Raise your bid to between $10,000,000 and $10,025,000. | ||
| c. Raise your bid above $10,025,000. | ||
| d. Lower your bid to $9,975,000. |
Question
41
Suppose you consider bidding at a government auction where the bids are sealed in envelopes with only one chance to bid. The winning bid gets the job and
all others receive nothing. You intend to bid on a job at a price of $10 million, and you know that your cost to complete the job is $9 million. As you are
about to submit the bid, you find out that a government official will have to be bribed $1 million to start the job. If the probability that you'll win is
10 percent, what is the rational course of action?
Choose one answer.
| a. Place the bid, knowing that there is only a 10 percent chance you will get the job anyway. | ||
| b. Wait and see how many others have placed bids to see if the probability of winning has changed. | ||
| c. Place a bid, but only if you are a risk lover. | ||
| d. Do not place a bid in this auction. |
Question
42
Suppose you are considering buying a one-year debenture priced at $10,000 yielding 7 percent a year. There is a 10 percent chance the issuer will default
on the payments and principal. What is your best course of action?
Choose one answer.
| a. Buy the debenture because the expected return is at least $700. | ||
| b. Buy the debenture because the expected return is greater than $0. | ||
| c. Don't buy the debenture because the expected return is effectively $0. | ||
| d. Don't buy the debenture because the expected return is negative. |
Question
43
Suppose you buy a one-year insured debenture priced at $10,000 yielding 3 percent a year. There is a 10 percent chance the issuer will default on the
payments only and return your principal. What is your expected return?
Choose one answer.
| a. $10,000 | ||
| b. $10,270 | ||
| c. $10,300 | ||
| d. $9,270 |
Question
44
On January 5, you buy a 10-year corporate bond yielding 5.5 percent. On January 6, the Central Bank of the United States uses monetary policy to lower the
rate on benchmark 10-year Treasuries from 2.5 percent to 1.5 percent. What is the new risk premium?
Choose one answer.
| a. 1.5 percent | ||
| b. 3 percent | ||
| c. 4 percent | ||
| d. 5.5 percent |
Question
45
Suppose you are building an economic model to help decide how to pick the best investment to save for college. The entire proceeds of the investment will
be used to pay college tuition. The rate of inflation is expected to be 2 percent a year for three years. The price of college tuition is expected to
increase by 5 percent a year. The nominal interest rate on AAA-rated government three-year bonds is 3 percent. Which rates are most appropriate to
incorporate into your model?
Choose one answer.
| a. The expected inflation rate, the expected price of college tuition, and the government riskless rate of return | ||
| b. The expected inflation rate and the government riskless rate of return | ||
| c. The expected inflation rate and the expected price of college tuition | ||
| d. The expected price of college tuition. |
Question
46
When are expected real "r" and nominal rates "i" the same when an investor is risk-loving?
Choose one answer.
| a. When r = i | ||
| b. When r < i | ||
| c. When r > i | ||
| d. When r = i = 0. |
Question
47
In choosing an economic tool to calculate compound interest, which mathematical operation is part of the equation?
Choose one answer.
| a. Common log | ||
| b. Natural log | ||
| c. Binary log | ||
| d. Cobb-Douglas log |
Question
48
What economic tool best describes how a yield curve changes?
Choose one answer.
| a. Derivative with respect to time | ||
| b. Partial derivative with respect to rates | ||
| c. Derivative with respect to rates | ||
| d. Partial derivative holding the riskless rate constant. |
Question
49
Suppose countries Q and Z have completely free trade. If the price of an ounce of silver is $10 in country Q and $10.05 in country Z, when will arbitrage
occur given shipping costs of "s" cents?
Choose one answer.
| a. When s = 5. | ||
| b. When 0 < s < 5. | ||
| c. When 0 = s = 5. | ||
| d. When s = 5. |
Question
50
The compound rate of interest on a savings account is 4 percent. Inflation is 1 percent. You deposit $250,000 and leave it in the account for three years.
If the bank charges you a one-time $99 fee to open the account, what will be the value in the account at the end of three years?
Choose one answer.
| a. $281,104 | ||
| b. $281,704 | ||
| c. $281,709 | ||
| d. $282,704 |
Question
51
Suppose Tom can either hunt for birds 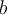 or forage
for wild berries
or forage
for wild berries 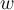 on his isolated island property.
He can catch nine birds or gather two pounds of berries in an hour. He only has eight hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch nine birds or gather two pounds of berries in an hour. He only has eight hours a week to devote to these activities. His utility function for
birds and berries is 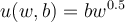 . What is the equation of
his production possibilities frontier?
. What is the equation of
his production possibilities frontier?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
52
Suppose Fran can either hunt for birds 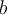 or forage
for wild berries
or forage
for wild berries 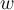 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 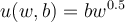 . Which point is not Pareto
efficient?
. Which point is not Pareto
efficient?
Choose one answer.
| a. (20, 40) | ||
| b. (2, 36) | ||
| c. (7, 26) | ||
| d. (9, 24) |
Question
53
Suppose Fran can either hunt for birds 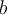 or forage
for wild berries
or forage
for wild berries 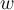 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 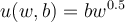 . What is the marginal rate
of transformation of birds for berries?
. What is the marginal rate
of transformation of birds for berries?
Choose one answer.
|
a. |
||
|
b. |
||
| c. 2 | ||
| d. -2 |
Question
54
Suppose Tom can either hunt for birds 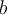 or forage
for wild berries
or forage
for wild berries 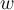 on his isolated island property.
He can catch nine birds or gather two pounds of berries in an hour. He only has eight hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch nine birds or gather two pounds of berries in an hour. He only has eight hours a week to devote to these activities. His utility function for
birds and berries is 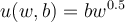 . What is the marginal rate
of transformation of birds for berries?
. What is the marginal rate
of transformation of birds for berries?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
55
Suppose Fran can either hunt for birds 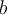 or forage
for wild berries
or forage
for wild berries 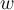 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 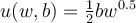 . What is the marginal rate
of transformation of birds for berries?
. What is the marginal rate
of transformation of birds for berries?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
56
Suppose Fran can either hunt for birds 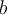 or forage
for wild berries
or forage
for wild berries 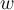 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 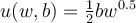 . What is the expression for
b when the marginal rate of substitution of birds for berries is equal to the marginal rate of transformation of birds for berries?
. What is the expression for
b when the marginal rate of substitution of birds for berries is equal to the marginal rate of transformation of birds for berries?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
57
Suppose Fran can either hunt for birds 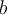 or forage
for wild berries
or forage
for wild berries 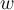 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 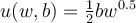 . Using the information from
the production possibilities frontier, what is the Pareto optimal allocation for birds?
. Using the information from
the production possibilities frontier, what is the Pareto optimal allocation for birds?
Choose one answer.
| a. 18 | ||
| b. 28 | ||
| c. 38 | ||
| d. 48 |
Question
58
Which mathematical tool do economists use to measure the marginal rate of substitution?
Choose one answer.
| a. Ratio | ||
| b. Partial differentiation | ||
| c. Implicit differentiation | ||
| d. All of the above. |
Question
59
Suppose the government in a closed country imposes a lump sum tax of $9,000 on some people (sp) and redistributes the income to other people (op) in
society. After the tax is levied and distributed, what is the deadweight loss to society?
Choose one answer.
| a. $0 | ||
| b. +$9,000*sp | ||
| c. -$9,000*op | ||
| d. The answer cannot be determined by the information given. |
Question
60
Suppose the government in a closed country imposes a tax of 5 percent on working people's wages (w) and redistributes the tax to nonworking people (n) in
society as a lump sum distribution. This causes working people to reduce labor by 10 percent. After the tax is levied and distributed, what is the
deadweight loss to society relative to a lump sum tax system?
Choose one answer.
| a. $0 | ||
| b. 0.005w | ||
| c. 0.05w | ||
| d. 0.10w |
Question
61
Suppose the government in a closed country imposes a tax of 12 percent on working people's wages (w) and redistributes the tax to nonworking people (n) in
society as a lump sum distribution. This causes working people to reduce labor by 6 percent. After the tax is levied and distributed, what is the
deadweight loss to society relative to a lump sum tax system?
Choose one answer.
| a. $0 | ||
| b. 0.06w | ||
| c. 0.12w | ||
| d. 0.18w |
Question
62
Suppose you are shopping at a farmers' market at 4:59 p.m. It closes at 5 p.m. At the end of the day, the farmer will have to discard her lettuce. The
price of the lettuce is $2.50. You are willing to pay $1.00 for the lettuce. What is the Pareto optimal price for the lettuce?
Choose one answer.
| a. $0 | ||
| b. $1 | ||
| c. $2.50 | ||
| d. The information cannot be determined by the information given. |
Question
63
Suppose Fran can either hunt for birds 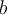 or forage
for wild berries
or forage
for wild berries 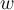 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 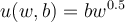 . What is the marginal rate
of transformation of birds for berries?
. What is the marginal rate
of transformation of birds for berries?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
64
Suppose Fran can either hunt for birds 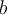 or forage
for wild berries
or forage
for wild berries 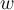 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 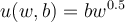 . To consume at a Pareto
optimal amount of 42 birds, how many more or less hours must Tom devote to these activities?
. To consume at a Pareto
optimal amount of 42 birds, how many more or less hours must Tom devote to these activities?
Choose one answer.
|
a. |
||
|
b. |
||
| c. 2 hours more | ||
| d. 2 hours less |
Question
65
Which economic tool describes the set of all Pareto efficient combinations of goods?
Choose one answer.
| a. Any utility function | ||
| b. A marginal rate of substitution | ||
| c. A budget line. | ||
| d. Only a Cobb-Douglas utility function |
Question
66
Given a utility function defined as 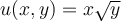 , what is the
marginal utility with respect to good
, what is the
marginal utility with respect to good 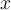 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
67
Suppose Fran can either hunt for birds 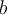 or forage
for wild berries
or forage
for wild berries 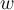 on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is
on his isolated island property.
He can catch four birds or gather two pounds of berries in an hour. He only has 10 hours a week to devote to these activities. His utility function for
birds and berries is 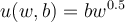 . What is the slope of his
production possibilities frontier?
. What is the slope of his
production possibilities frontier?
Choose one answer.
|
a. |
||
|
b. |
||
| c. 2 | ||
| d. -2 |
Question
68
Consider this duopoly game. Each player can either take a cookie off a table or agree to share 16 cookies. What is the dominant strategy's outcome?
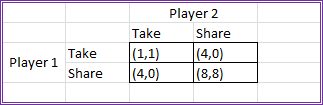
Choose one answer.
| a. Player 1 takes and Player 2 takes. | ||
| b. Player 1 takes and Player 2 shares. | ||
| c. Player 1 shares and Player 2 takes. | ||
| d. Player 1 shares and Player 2 shares. |
Question
69
Consider this duopoly game. Each player can either take a cookie off a table or agree to share 16 cookies. What is the Pareto optimal outcome?

Choose one answer.
| a. Player 1 takes and Player 2 takes. | ||
| b. Player 1 takes and Player 2 shares. | ||
| c. Player 1 shares and Player 2 takes. | ||
| d. Player 1 shares and Player 2 shares. |
Question
70
Consider this duopoly game. Each player can either take a cookie off a table or agree to share 16 cookies. What factor would most likely drive a Pareto
optimal solution?

Choose one answer.
| a. The relatively high payoff for cooperation | ||
| b. The lack of a payoff in a nondominant mixed solution | ||
| c. The degree of trust between the players driving the underlying probabilities | ||
| d. Parity in the take-take outcome |
Question
71
Consider this game. Given that p is the probability that Player 1 will choose N and Player 2 will choose Y, which of the following is a pure strategy Nash
equilibrium?
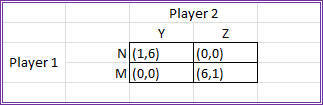
Choose one answer.
| a. p = 0 and q = 1 | ||
| b. p = 1 and q = 0 | ||
| c. p = 0 and q = 0 | ||
| d. p = 0.5 and q = 0.5 |
Question
72
Consider this game. Given that p is the probability that Player 1 will choose N and Player 2 will choose Y, which of the following is a mixed strategy Nash
equilibrium?

Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There is no mixed strategy Nash equilibrium. |
Question
73
Consider this game. Given that p is the probability that Player 1 will choose N and Player 2 will choose Y, which of the following is a pure/mixed strategy
Nash equilibrium?

Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There is no pure/mixed strategy Nash equilibrium. |
Question
74
Consider this game. Given that p is the probability that Player 1 will choose N and Player 2 will choose Y, what is the result of partial cooperation
(where one player cooperates and the other does not)?

Choose one answer.
| a. They divide up the seven things equally. | ||
| b. They divide up the seven things unequally. | ||
| c. They both get nothing. | ||
| d. There is an ultimate winner receiving all seven things. |
Question
75
Consider this game. Given that p is the probability that Player 1 will choose N and Player 2 will choose Y, which mathematical tool is used to evaluate
possible Nash equilibriums for Player 1?

Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
76
Consider this game. Given that p is the probability that Player 1 will choose N and Player 2 will choose Y, which mathematical tool is used to evaluate
possible Nash equilibriums for Player 2?

Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
77
Given a multistage game, what three economic tools are you most likely to use to find Nash equilibrium?
Choose one answer.
| a. Expected value operator, partial derivative, Gantt chart | ||
| b. Expected value operator, double derivative, decision tree | ||
| c. Expected value operator, partial derivative, decision tree | ||
| d. First derivative, second derivative, partial derivative |
Question
78
Suppose 50 people at an auction are bidding on a piece of land that is known to contain platinum deposits. The low bid is $10 million, the average bid is
$14 million, and the high bid is $19 million. What is the value of the winner's curse?
Choose one answer.
| a. $4 million | ||
| b. $5 million | ||
| c. $9 million | ||
| d. The answer cannot be determined because we need to know the second highest bid. |
Question
79
Suppose 100 people at an auction are bidding on a piece of land that is known to contain silver deposits. The low bid is $3 million, the average bid is $5
million, and the high bid is $9 million. What is the value of the winner's curse?
Choose one answer.
| a. $2 million | ||
| b. $4 million | ||
| c. $9 million | ||
| d. There is no curse. |
Question
80
Suppose at an all-pay auction, the low bid is $9 million, the middle bid is $10 million, and the high bid is $11 million. What is the realized market value
to the person selling?
Choose one answer.
| a. $9 million | ||
| b. $10 million | ||
| c. $11 million | ||
| d. $30 million |
Question
81
Suppose at an all-pay auction, the low bid is $3 million, the middle bid is $7 million, and the high bid is $8 million. What is the realized market value
to the person selling?
Choose one answer.
| a. $15 million | ||
| b. $18 million | ||
| c. $28 million | ||
| d. There is no realized market value to the person selling. |
Question
82
Suppose at an all-pay sealed bid auction, there are 30 bids. The first 10 participants bid $3 million. Participants 11 to 20 bid $5 million. And the last
10 bid $7 million. What is the winner's curse for bidder number 11?
Choose one answer.
| a. $0 million | ||
| b. $2 million | ||
| c. $5 million | ||
| d. There is no winner's curse at an all-pay sealed bid auction. |
Question
83
Suppose you bid on a Ming vase in a first-price sealed bid auction. You value the vase at $3 million. Your probability of winning is 10 percent. What is
your expected value of bidding $2 million?
Choose one answer.
| a. $0 | ||
| b. $10,000 | ||
| c. $100,000 | ||
| d. $1,000,000 |
Question
84
Suppose you bid on a diamond in a first-price sealed bid auction. You value the diamond at $10 million. Your probability of winning is 90 percent. What is
your expected value of bidding $9 million?
Choose one answer.
| a. $0 | ||
| b. $900,000 | ||
| c. $999,000 | ||
| d. $1,000,000 |
Question
85
Suppose you bid on a Ming vase in a first-price sealed bid auction. You value the vase at $3 million. Your probability of winning is 10 percent. What is
your expected value of bidding $3 million?
Choose one answer.
| a. $0 | ||
| b. $10,000 | ||
| c. $100,000 | ||
| d. $1,000,000 |
Question
86
In backward induction, a likely outcome of a game can be predicted. What can we say about the likely outcome?
Choose one answer.
| a. It will be not Pareto optimal. | ||
| b. It will not coincide with the same solution as if the game played out from the beginning. | ||
| c. It will not be Pareto optimal as long as it's the same solution as if the game played out from the beginning. | ||
| d. It can be only compared with other outcomes to determine Pareto optimality. |
Question
87
Given a demand curve 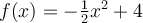 , what is the price
elasticity at point (2,2)?
, what is the price
elasticity at point (2,2)?
Choose one answer.
| a. 0.5 | ||
| b. 1 | ||
| c. 2 | ||
| d. 3 |
Question
88
Given an individual demand curve 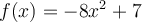 with 20 total
consumers in the market, what is the slope of the market demand curve?
with 20 total
consumers in the market, what is the slope of the market demand curve?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. -320 |
Question
89
Given a utility function, 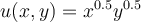 , what is the slope of
the indifference curve at a satisfaction level of 4?
, what is the slope of
the indifference curve at a satisfaction level of 4?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
90
To determine the slope of an indifference curve at a particular point for two goods, which mathematical tool is most appropriate?
Choose one answer.
| a. Partial derivative | ||
| b. First derivative | ||
| c. Second derivative | ||
| d. Cobb-Douglas utility function |
Question
91
Given a utility function, 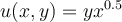 , what is the slope of
the indifference curve at a satisfaction level of 200?
, what is the slope of
the indifference curve at a satisfaction level of 200?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
92
Given a utility function, 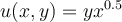 , with prices of (3,4),
what is the optimization problem in order to reach a satisfaction level of 500?
, with prices of (3,4),
what is the optimization problem in order to reach a satisfaction level of 500?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
93
Which mathematical technique can be used to solve the consumer's optimization problem?
Choose one answer.
| a. Lagrangian | ||
| b. Eulerian | ||
| c. Hamiltonian | ||
| d. Frunze's periphrastic |
Question
94
If supply is 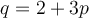 and demand is
and demand is 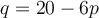 , then what is the market equilibrium price?
, then what is the market equilibrium price?
Choose one answer.
| a. 1 | ||
| b. 2 | ||
| c. 3 | ||
| d. 4 |
Question
95
If supply is 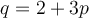 and demand is
and demand is 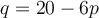 , then what is the market equilibrium quantity?
, then what is the market equilibrium quantity?
Choose one answer.
| a. 2 | ||
| b. 4 | ||
| c. 6 | ||
| d. 8 |
Question
96
If supply is 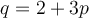 and demand is
and demand is 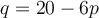 , then what is the market's total revenue?
, then what is the market's total revenue?
Choose one answer.
| a. 4 | ||
| b. 8 | ||
| c. 16 | ||
| d. 32 |
Question
97
If supply is 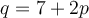 and demand is
and demand is 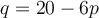 , then what is the equation for price elasticity of demand at market
equilibrium?
, then what is the equation for price elasticity of demand at market
equilibrium?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
98
If supply is 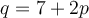 and demand is
and demand is 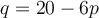 , and the government imposes a $1 tax on buyers, what are the new
supply and demand curves?
, and the government imposes a $1 tax on buyers, what are the new
supply and demand curves?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
99
Given a demand curve 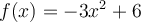 , what is the price
elasticity at point (1,3)?
, what is the price
elasticity at point (1,3)?
Choose one answer.
| a. 0.5 | ||
| b. 1 | ||
| c. 2 | ||
| d. 3 |
Question
100
Given an individual demand curve 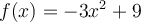 with 100 total
consumers in the market, what is the slope of the market demand curve?
with 100 total
consumers in the market, what is the slope of the market demand curve?
Choose one answer.
| a. -300 | ||
|
b. |
||
|
c. |
||
|
d. |