1
A collection of data yields a correlation coefficient of 0.95, indicating which of the following?
Choose one answer.
|
a. The data points have a slope close to 1. |
||
|
b. The data points are normally distributed. |
||
|
c. The data points are nearly linear. |
||
|
d. The data points have very little correlation. |
Question 2
Calculate the average rate of change of j(x) = x3 - 5 over the interval [-2, 6].
Choose one answer.
|
a. 0.0202 |
||
|
b. 0.0357 |
||
|
c. 28 |
||
|
d. 48 |
Question 3
Consider a function f(x) = axn + b, where a, b, and n are integers larger than 1. Which of the following statements is true?
Choose one answer.
|
a. If n is odd, there will be an absolute maximum. |
||
|
b. If n is even, there will be an absolute minimum. |
||
|
c. There will be neither an absolute maximum nor an absolute minimum. |
||
|
d. The existence of extremes cannot be determined without more information. |
Question 4
Consider the function 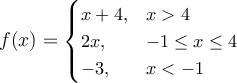 and find f[f(2)].
and find f[f(2)].
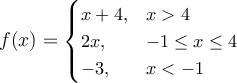 and find f[f(2)].
and find f[f(2)].
Choose one answer.
|
a. -3 |
||
|
b. -1 |
||
|
c. 4 |
||
|
d. 8 |
Question 5
Consider the function f(x)=x2-3x-4 and find f(x+3).
Choose one answer.
|
a. f(x+3)=x2+3x+1. |
||
|
b. f(x+3)=x2+3x-4. |
||
|
c. f(x+3)=x2-3x. |
||
|
d. f(x+3)=x2-3x-1. |
Question 6
Find the domain of 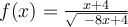 .
.
Choose one answer.
|
a. x ≠ |
||
|
b. x ≠ 4 |
||
|
c. x< |
||
|
d. |
Question 7
The expression log3 7 is equal to:
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 8
The line that passes through the points (-7, -6.75), (3, -14.25), and (-2, -10.5), has which of the following characteristics?
Choose one answer.
|
a. Positive slope and positive y-intercept |
||
|
b. Positive slope and negative y-intercept |
||
|
c. Negative slope and positive y-intercept |
||
|
d. Negative slope and negative y-intercept |
Question 9
What is the domain and range of the function g(x) = 4x2 - 11.5?
Choose one answer.
|
a. The domain and the range are the same: the set of all real numbers. |
||
|
b. The domain and the range are the same: [11.5, +∞). |
||
|
c. The domain is [-11.5, +∞); the range is all real numbers. |
||
|
d. The domain is all real numbers; the range is [-11.5, +∞). |
Question 10
Which of the following relations describes a function of x?
Choose one answer.
|
a. y = 3x + 1 |
||
|
b. y = (3x + 1)2 -11 |
||
|
c. x = y |
||
|
d. All of these |
Question 11
Which set identifies some of the places where the rational function 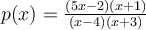 is defined?
is defined?
Choose one answer.
|
a. {2, 4, 6, 8} |
||
|
b. {-1, -3, -5, -7} |
||
|
c. {-4,-3, -2, -1, 0, 1, 2, 3} |
||
|
d. {-2, -, 0, 1, 2} |
Question 12
Find the value of x such that m(x) = 3 if m(x) = 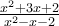
Choose one answer.
|
a. -3 |
||
|
b. -1 |
||
|
c. 2 |
||
|
d. 4 |
Question 13
Find x such that g(x) = 7 : g(x) = 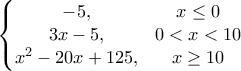
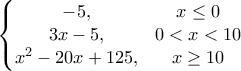
Choose one answer.
|
a. -5 |
||
|
b. 4 |
||
|
c. 10 |
||
|
d. The answer is irrational. |
Question 14
Solve (4x - 5)(4x2 + 15x - 4) 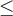 0.
0.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. (0.25, 1.25] |
||
|
d. |
Question 15
Solve 7x = 8.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 16
Solve for c: If a = bc, then c =
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 17
Solve for x: 2x+3 = 32x-1.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 18
Solve for x: 2x+5 = 12.
Choose one answer.
|
a. x = log 6 - 5 |
||
|
b. x = |
||
|
c. x = |
||
|
d. x = |
Question 19
Solve for x: log2x = 3 - log2(x - 2).
Choose one answer.
|
a. x = -2 |
||
|
b. x = -2 or 4 |
||
|
c. x = 4 |
||
|
d. x is undefined |
Question 20
Solve the inequality p4 - p3 - 20p2< 0.
Choose one answer.
|
a. [-4, 5] |
||
|
b. (-4, 5) |
||
|
c. (-4, 0) |
||
|
d. |
Question 21
Solve the inequality 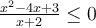 .
.
Choose one answer.
|
a. [1, 3] |
||
|
b. |
||
|
c. [-2, 3] |
||
|
d. |
Question 22
Consider a function f(x) = axn + bx, where a , b and n are integers larger than one. Which of the following statements is true?
Choose one answer.
|
a. If n is odd, the ends of the graph both tend in the positive direction. |
||
|
b. If n is even, the ends of the graph both tend in the positive direction. |
||
|
c. The ends of the graph will both tend in different directions. |
||
|
d. The end behavior cannot be determined without more information. |
Question 23
Consider the function h(x) = logbx, where x is a positive real number. Which of the following statements is true?
Choose one answer.
|
a. The point (1, 0) is on h(x). |
||
|
b. The right-hand end behavior of h(x) gets large toward positive infinity. |
||
|
c. The domain of h(x) is all positive real numbers. |
||
|
d. All of these. |
Question 24
Given the function g(x), identify a function with a graph two units to the left and five units down.
Choose one answer.
|
a. g(x-5) + 2 |
||
|
b. g(x) - 3 |
||
|
c. g(x + 5) - 2 |
||
|
d. g(x + 2) - 5 |
Question 25
The graph of an exponential function:
Choose one answer.
|
a. usually has both positive and negative y- values. |
||
|
b. contains the point (0, 1). |
||
|
c. has a horizontal asymptote at y = 1. |
||
|
d. has a domain of positive real numbers. |
Question 26
The graph of the function 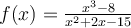 will have a vertical asymptote at:
will have a vertical asymptote at:
Choose one answer.
|
a. 2. |
||
|
b. 3. |
||
|
c. 5. |
||
|
d. 8. |
Question 27
What kind of function is depicted in the graph?


Choose one answer.
|
a. Polynomial |
||
|
b. Piecewise |
||
|
c. Odd |
||
|
d. Even |
Question 28
What kind of function is depicted in the graph?
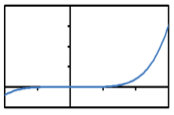

Choose one answer.
|
a. Exponential |
||
|
b. Rational |
||
|
c. Quadratic |
||
|
d. Cubic |
Question 29
What kind of function is depicted in the graph?
Choose one answer.
|
a. Polynomial |
||
|
b. Piecewise |
||
|
c. Logarithmic |
||
|
d. Even |
Question 30
Which of the following shows the graph of a logarithmic function?
A.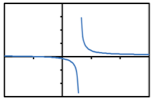 B.
B. 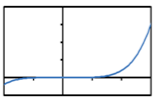
C.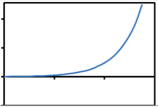 D.
D. 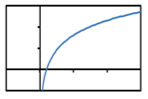
A.
 B.
B. 
C.
 D.
D. 
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question 31
Which of the following shows the graph of a rational function?
A.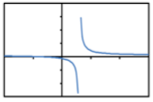 B.
B. 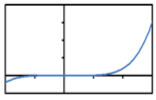
C.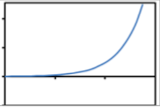 D.
D. 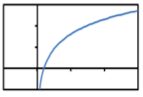
A.
 B.
B. 
C.
 D.
D. 
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question 32
Consider m(k) = 4x3 - 7. Find m-1(k).
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 33
Consider the function f(x) = bx, where b is a positive real number. What is the domain of f-1(x)?
Choose one answer.
|
a. All real numbers |
||
|
b. x > 0 |
||
|
c. x > b |
||
|
d. 0 < x < b |
Question 34
Consider the two inverse functions h(x) and h-1(x). Which of the following is true about graphing the two functions?
Choose one answer.
|
a. The two graphs make a mirror image over the x-axis. |
||
|
b. The two graphs make a mirror image over the y-axis. |
||
|
c. The two graphs make a mirror image over the line y = x. |
||
|
d. The two graphs make a mirror image over the line y = -x. |
Question 35
Find the inverse of the function 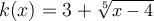 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 36
If  and
and 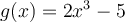 ,
, 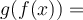
Choose one answer.
|
a. 1.5 (x + 5). |
||
|
b. .5(x + 5). |
||
|
c. x3 – 5. |
||
|
d. x. |
Question 37
Let f(x) = x - 3 and g(x) = 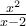 . Find g(f(3)).
. Find g(f(3)).
Choose one answer.
|
a. 0 |
||
|
b. -0.5 |
||
|
c. 6 |
||
|
d. 9 |
Question 38
Let 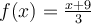 and
and 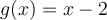 . Find
. Find 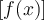 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 39
Use the following three functions to determine (g(h(x))): f(x) = x + 2, g(x) = ln (x-5), h(x) = x-1.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 40
Use the following three functions to determine f(g(h(3))): f(x) = x - 4, g(x) = x2, h(x) = 2x.
Choose one answer.
|
a. 2 |
||
|
b. 4 |
||
|
c. 10 |
||
|
d. 32 |
Question 41
Which of the following is true about a one-to-one function?
Choose one answer.
|
a. It is always increasing or decreasing. |
||
|
b. It has an inverse. |
||
|
c. It does not have an inverse. |
||
|
d. It is its own inverse. |
Question 42
A ball is hurled upward from the top of a building. Its height at time t (in seconds) can be described by the function H(t)=-16t2+64t+120. If the maximum height of the ball is 150 feet, how many seconds did it take for the ball to reach its maximum height?
Choose one answer.
|
a. 1 second |
||
|
b. 1.5 seconds |
||
|
c. 2 seconds |
||
|
d. 2.5 seconds |
Question 43
A function t(x) has x-intercepts at -4 and 9. Where are the intercepts of t(x - 5)?
Choose one answer.
|
a. At -4 and 9. |
||
|
b. At 4 and -9. |
||
|
c. At 1 and 14. |
||
|
d. At 20 and -45. |
Question 44
A polynomial function that has three different roots:
Choose one answer.
|
a. can be inverted only if the domain is restricted. |
||
|
b. passes both the vertical and the horizontal line tests |
||
|
c. will have no more than two relative maximums. |
||
|
d. will have no more than two relative minimums. |
Question 45
Find the roots of the function f(x)=4x3+8x2-21x.
Choose one answer.
|
a. 0, 3, 7 |
||
|
b. 4, 8, -21 |
||
|
c. 2, |
||
|
d. -3.5, -1.5, 0 |
Question 46
Find the x-intercepts of the function f(x)=3x2-15x-52.
Choose one answer.
|
a. 2 and 7 |
||
|
b. -2 and 7 |
||
|
c. -2 and -7 |
||
|
d. 2 and -7 |
Question 47
One root of the function g(x)=3x3-12x2-36x:
Choose one answer.
|
a. is at -2, and the function is positive on the left and negative on the right. |
||
|
b. is at 0, and the function is negative on the left and positive on the right. |
||
|
c. is at 6, and the function is positive on the left and negative on the right. |
||
|
d. is at -36, and the function is negative on the left and positive on the right. |
Question 48
The following statements refer to the function y=ax2+bx+c. Which statement is true?
Choose one answer.
|
a. The function has a vertex at |
||
|
b. The function has two roots. |
||
|
c. The range of the function is all positive real numbers. |
||
|
d. The function has one relative maximum. |
Question 49
The function f(x)=|x-a|+b has a vertex at which of the following?
Choose one answer.
|
a. (a, b) |
||
|
b. (a, -b) |
||
|
c. (-a, b) |
||
|
d. (-a,-b) |
Question 50
The function h(x)=2x-8x-24:
Choose one answer.
|
a. has a minimum at 2. |
||
|
b. has a minimum at -2. |
||
|
c. has a maximum at 2. |
||
|
d. has a maximum at -2. |
Question 51
The quadratic function f(x) = -5x2 + 30:
Choose one answer.
|
a. has a maximum at -6. |
||
|
b. has a minimum at 1.5. |
||
|
c. has a minimum at -1.5. |
||
|
d. has a maximum at 0. |
Question 52
A printer makes reproductions of a series of pictures. They are all different sizes, but each picture has a height that is twice the length of the width. The printer wants to maintain the original proportions but make the area of each reproduction to be half as large as the area of its original picture. Develop a function (R(w)) that would indicate the width of a final reproduction as a function of the width (w) of the original picture.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 53
A radioactive isotope has a half-life of 250 years. How long will it take, approximately, for the substance to be at one third of its original strength?
Choose one answer.
|
a. 160 years |
||
|
b. 300 years |
||
|
c. 340 years |
||
|
d. 400 years |
Question 54
A woman throws a stone upward. Its height above the ground at t seconds can be described by h(t) = -16t2 + 48t + 6, where h is in feet. What is the maximum height that the stone can reach?
Choose one answer.
|
a. 32 feet |
||
|
b. 42 feet |
||
|
c. 48 feet |
||
|
d. 56 feet |
Question 55
An investment compounded continuously tripled in five years. What was the approximate interest rate?
Choose one answer.
|
a. 11% |
||
|
b. 15% |
||
|
c. 18% |
||
|
d. 22% |
Question 56
Newton’s law of cooling indicates the temperature of an object and can be described by the function 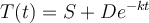 where S is the surrounding temperature, D is the difference between the initial temperature and the surrounding temperature, t is the time elapsed, and k is the cooling constant. If tea is served at 200 degrees and cools to 150 degrees in 10 minutes, what is the value of the cooling constant?
where S is the surrounding temperature, D is the difference between the initial temperature and the surrounding temperature, t is the time elapsed, and k is the cooling constant. If tea is served at 200 degrees and cools to 150 degrees in 10 minutes, what is the value of the cooling constant?
Choose one answer.
|
a. 0.04465 |
||
|
b. 0.04532 |
||
|
c. 0.04687 |
||
|
d. 0.04796 |
Question 57
Squares with sides of size x are cut from the four corners of a rectangular piece of cardboard so that the cardboard can be folded into an open-topped rectangular box. The original cardboard is 20 × 24. Which function describes the volume of the resulting box as a function of x?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 58
The cost of producing “doomflots” is $325 for equipment plus another $32 for materials and labor for each one produced. How many “doomflots” need to be produced such that the average cost per “doomflot” is less than $50?
Choose one answer.
|
a. 9 |
||
|
b. 10 |
||
|
c. 18 |
||
|
d. 19 |
Question 59
The cougar population in Oregon was estimated to be 5,000 animals in 2006, having grown from about 3,150 in 1996. In what year would we expect a population of 7,500?
Choose one answer.
|
a. 2010 |
||
|
b. 2014 |
||
|
c. 2018 |
||
|
d. 2024 |
Question 60
The Roman Census under Emperor Augustus in 28 BC was listed at 4,063,000. Twenty years later in 8 BC, another census listed the population at 4,233,000. Assuming the figures are accurate, what was the growth rate of Rome in that 20-year period?
Choose one answer.
|
a. 0.77% |
||
|
b. 0.78% |
||
|
c. 7.7% |
||
|
d. 7.8% |
Question 61
To the nearest tenth of a year, how long will it take for an investment of $2,000 to double if the interest rate is 3.5% per year, compounded continuously?
Choose one answer.
|
a. 17.6 |
||
|
b. 18.4 |
||
|
c. 19.8 |
||
|
d. 20.2 |
Question 62
A city engineer is trying to model the shape of a hill using a quadratic function. She places a grid over a photograph of the hill and finds the following points to describe the relation: (-1, -11), (-2, -11), and (0, -9). Which of the following will help the engineer find that function?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 63
Find a function to model the area of a rectangle as shown in the diagram. The point (x,y) is on the line 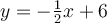 .
.


Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 64
Find an equation for a parabola that contains the points (-1, -11) and (3, -11) and contains an absolute maximum of -3.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 65
Find the function that fits the given points:
Choose one answer.
a. 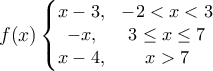 |
||
b. 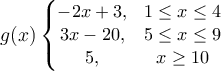 |
||
c. 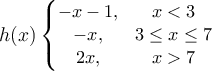 |
Question 66
Find the missing table values for 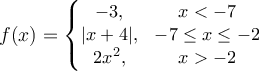

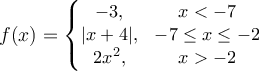
Choose one answer.
|
a. -3, 3, 1, 2, 2 |
||
|
b. -3, -3, -1, 2, -2 |
||
|
c. 3, -3, -1, -2, 2 |
||
|
d. 3, 3, 1, -2, -2 |
Question 67
Find the missing table values for 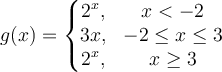

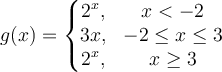
Choose one answer.
|
a. -8, 0, 8 |
||
|
b. - |
||
|
c. -8, 1, |
||
|
d. - |
Question 68
Find the missing table values for 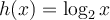 .
.

Choose one answer.
|
a. -1, 2, 4 |
||
|
b. undefined, 0, 1 |
||
|
c. undefined, 1, 2 |
||
|
d. 0.25, 2, 1 |
Question 69
If the average rate of change of a function between x = -2 and x = 5 is -7, then:
Choose one answer.
|
a. the function increases between -2 and 5. |
||
|
b. the function decreases between -2 and 5. |
||
|
c. the function passes from above the axis to below the axis. |
||
|
d. the function passes from below the axis to above the axis. |
Question 70
Two integers have a sum of 82 and a product of 1,680. Find an equation to model the relation.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 71
Which function is most likely associated with the following graph?
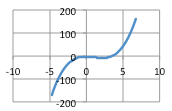

Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 72
A fly lights on the edge of an 18 ×12-inch picture frame and is x units away from a bottom corner, as designated by the star on the diagram. Which function describes how far the fly is from the top left corner?


Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 73
A gardener has 200 feet of fencing to use to enclose an area for a rectangular garden. By putting the garden against one wall of the house, only three sides need to be fenced. What is a function that would describe the area of the resulting garden space if x is the length of the side perpendicular to the wall of the house?
Choose one answer.
|
a. A(x)=200x-2x2 |
||
|
b. A(x)=x(200-x) |
||
|
c. A(x)=2x2-200x |
||
|
d. A(x)=2x(200x) |
Question 74
A party planner charges $200 plus $7.50 per person for parties up to 20 people. For groups larger than 20, the charge is $17 per person. For groups of more than 50, the party planner charges $16 for each additional person. Which piecewise function describes the cost of the party as a function of the number of people attending?
Choose one answer.
a. 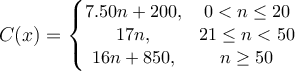 |
||
b. 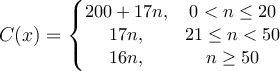 |
||
c. 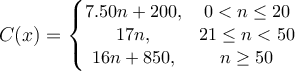 |
||
d. 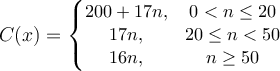 |
Question 75
A portion of fencing 100 feet long is cut into two pieces. One piece, which is x feet long, is used to enclose a square pen. The other piece is shaped into an enclosure as an equilateral triangle. What is the total area enclosed as a function of x?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 76
A rectangle has a perimeter of 36. Find a function A(w) to describe the area of the rectangle, based upon the width.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 77
A square park has 20-foot sides. It is surrounded by a sidewalk that is x feet wide. Which function describes the area of the sidewalk?


Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 78
A window is made up of a rectangle surmounted by a half circle. The height of the rectangle is 2.4 times the width. Determine a function A(w) to describe the area of the window as a function of the width, w.

Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 79
The population of rabbits on a farm grows exponentially. If there are currently 245 rabbits and the growth rate is 23%, find a function 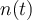 to describe the number of rabbits after t years.
to describe the number of rabbits after t years.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 80
The volume of a cylinder can be described by the function 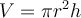 . Find a formula to describe the volume of a cylinder where the radius is three times the height.
. Find a formula to describe the volume of a cylinder where the radius is three times the height.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 81
Which of the following functions describes the total amount of money available after investing $5,000 at a rate of 2.3% for t years, compounded continuously?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |