|
A. A dependent quantity |
||
|
B. A rule that relates an input to exactly one output |
||
|
C. An independent quantity |
||
|
D. A combination of domain and range |
|
A. 125 |
||
|
B. 25 |
||
|
C. 1 |
||
|
D. 100 |
Determine which toolkit function has been transformed with a horizontal shift into the graph below.
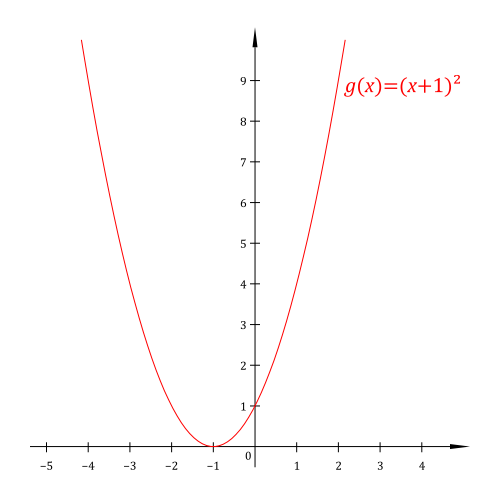
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
If the graph below is reflected vertically, shifted to the left by 1, and down by 3, what is the equation of the new graph?
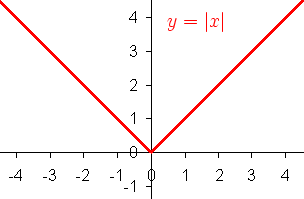
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Use the table below to find h-1(30).
| x | 15 | 30 | 45 | 60 |
| h(x) | 20 | 25 | 30 | 35 |
|
A. 15 |
||
|
B. 25 |
||
|
C. 45 |
||
|
D. 60 |
In the graph below of g(x), find g-1(2).
|
A. 1 |
||
|
B. 2 |
||
|
C. 3 |
||
|
D. 4 |
Determine the range for the piecewise function shown below in the domain [-0.5, 0.5].
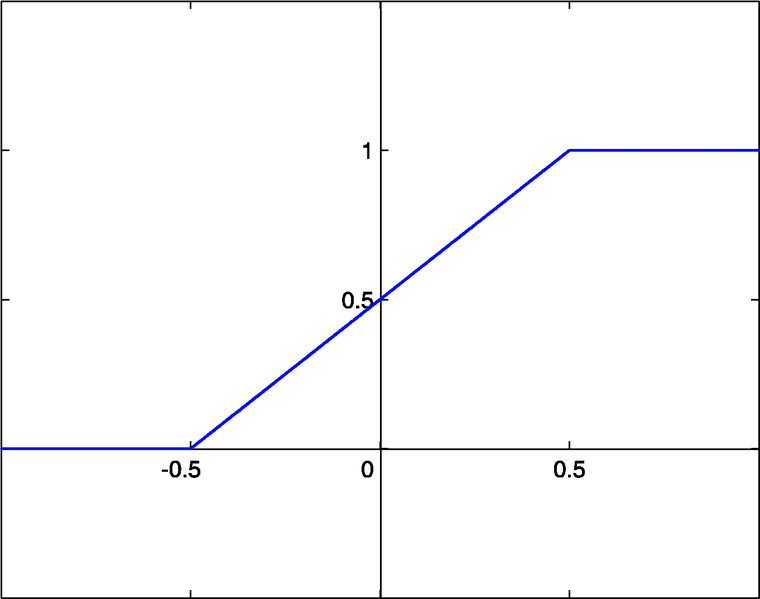
|
A. (1, 0) |
||
|
B. [0, 1] |
||
|
C. (-0.5, 0) |
||
|
D. (0, 0.5) |
|
A. x = -1.414, 1.414 |
||
|
B. x = -1.489, 1.489 |
||
|
C. x = 0 |
||
|
D. x = -0.213, 0.212 |
|
A. Increasing on |
||
|
B. Increasing on |
||
|
C. Increasing on |
||
|
D. Increasing on |
Which of the following tables demonstrates a one-to-one function?
Table 1:
| Input | Output |
| 3 | 8 |
| 2 | 16 |
| 3 | 24 |
Table 2:
| Input | Output |
| -2 | 3 |
| 0 | 2 |
| 2 | 3 |
Table 3:
| Input | Output |
| -1 | 1 |
| 0 | 0 |
| 2 | 2 |
|
A. Table 1 |
||
|
B. Table 2 |
||
|
C. Table 3 |
||
|
D. None of these |
Find the equation for the graph below.
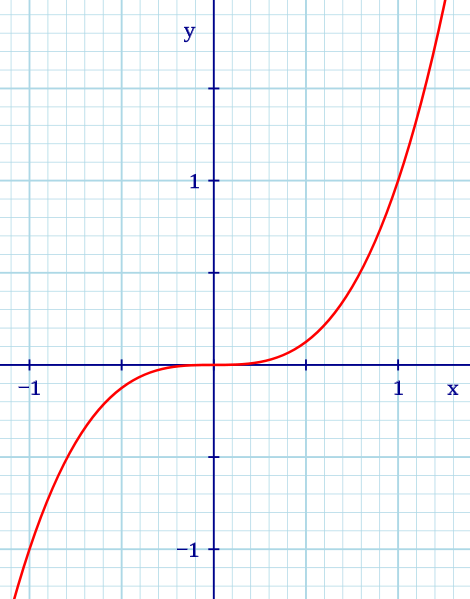
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Given the function t(s) = s3- 4s, evaluate t(4).
|
A. 48 |
||
|
B. 64 |
||
|
C. 112 |
||
|
D. -48 |
The graph below represents which toolkit function?
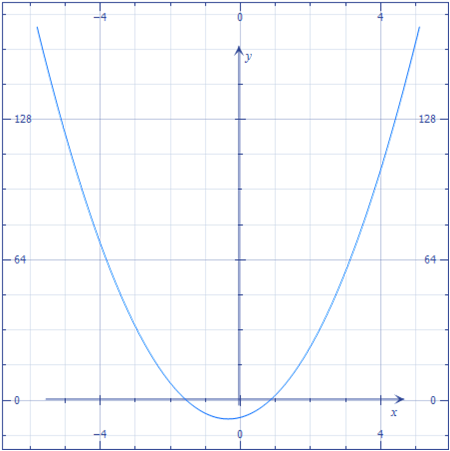
|
A. Reciprocal |
||
|
B. Square Root |
||
|
C. Absolute Value |
||
|
D. Quadratic |
|
a. a |
||
|
b. b |
||
|
c. c |
||
|
d. d |
Evaluate the domain and range of the function, ![]()
|
A. Domain: |
||
|
B. Domain: |
||
|
C. Domain: |
||
|
D. Domain: |
|
A. 10 |
||
|
B. 4 |
||
|
C. 8 |
||
|
D. 2 |
Which of the following is true for the graph below?
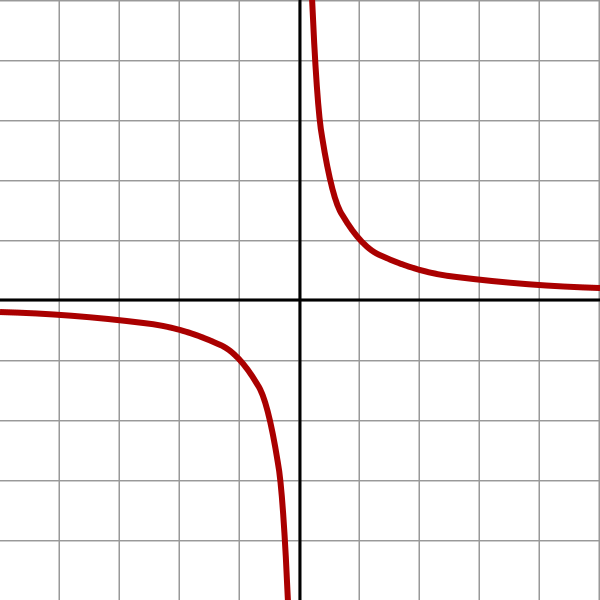
|
A. Decreasing on the intervals |
||
|
B. Concave down on |
||
|
C. Concave up on |
||
|
D. All of these |
Determine the inflection point(s) for the graph below.

|
A. x = -1 and x = 1 |
||
|
B. x = 0 |
||
|
C. x = |
||
|
D. None of these |
Using the tables below, evaluate f(g(2)) and g(f(1).
| x | f(x) |
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| x | g(x) |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
|
A. f(g(2)) = 2, g(f(1)) = 1 |
||
|
B. f(g(2)) = 6, g(f(1)) = 8 |
||
|
C. f(g(2)) = 12, g(f(1)) = 4 |
||
|
D. f(g(2)) = 3, g(f(1)) = 8 |
The graph below represents which toolkit function?

|
A. Reciprocal |
||
|
B. Square Root |
||
|
C. Absolute Value |
||
|
D. Quadratic |
Given the function ![]() , evaluate t(9).
, evaluate t(9).
|
A. 2 |
||
|
B. 12.17 |
||
|
C. 13 |
||
|
D. 17 |

|
A. -1 |
||
|
B. 2 |
||
|
C. 1 |
||
|
D. 0 |
Using the tables below, evaluate f(g(1)) and g(f(2)).
| x | f(x) |
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| x | g(x) |
| 1 | 2 |
| 3 | 5 |
| 6 | 10 |
| 9 | 12 |
|
A. f(g(1)) = 6, g(f(2)) = 10 |
||
|
B. f(g(2)) = 6, g(f(1)) = 9 |
||
|
C. f(g(2)) = 10, g(f(1)) = 6 |
||
|
D. f(g(2)) = 5, g(f(1)) = 8 |
|
A. f(h)=b |
||
|
B. f(3)=12 |
||
|
C. f(12)=3 |
||
|
D. f(1)=3 |
The table below represents the dollars (in millions) of Brand X candies sold per year. Use a graphing calculator to fit a linear equation to this data.
| Year | 1996 | 1998 | 2000 | 2002 | 2004 | 2006 | 2008 | 2010 | 2012 |
| $$ | 1.2 | 1.5 | 1.6 | 1.9 | 2.1 | 2.4 | 2.5 | 2.8 | 3.1 |
|
A. y = 228.34x - 0.115 |
||
|
B. y = 0.115x - 228.34 |
||
|
C. y = 5x - 22.49 |
||
|
D. Not linear |
|
A. 3, decreasing |
||
|
B. 2, decreasing |
||
|
C. -1.5, decreasing |
||
|
D. 1.5, increasing |
If f(x) is a linear function, find an equation for it given f(4) = -1 and f(9) = 2.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
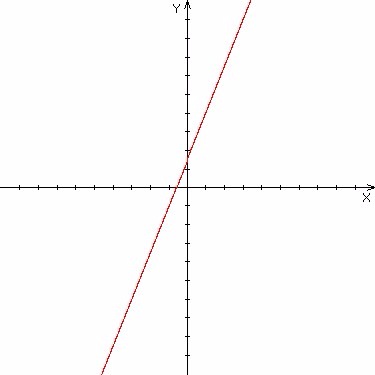
|
A. -0.5 |
||
|
B. 1 |
||
|
C. 2.5 |
||
|
D. -2.5 |
|
A. d(h) = 5h + 2 |
||
|
B. d(h) = h - 5 |
||
|
C. d(h) = 2h + 5 |
||
|
D. d(h) = 5 - 2h |
Assuming a scale of 1, determine which graph below represents the function y = 1 + 4x.
Graph A
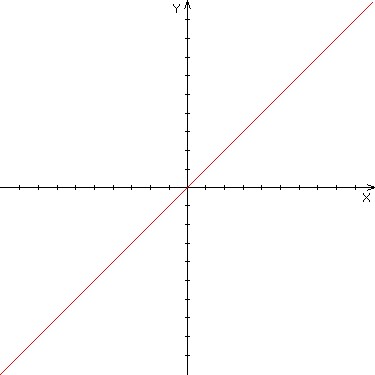
Graph B
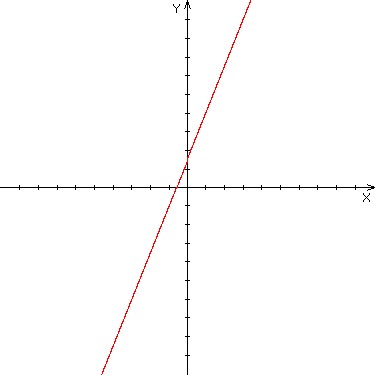
Graph C
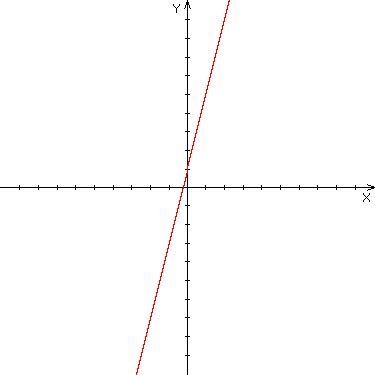
|
A. Graph A |
||
|
B. Graph B |
||
|
C. Graph C |
||
|
D. None of these |
Assuming a scale of 1, determine which graph below represents the function y = 1.5 + 2.5x.
Graph A

Graph B

Graph C

|
A. Graph A |
||
|
B. Graph B |
||
|
C. Graph C |
||
|
D. None of these |
|
A. y = 280 - 12.5x |
||
|
B. y = 255 + 12.5x |
||
|
C. y = 280 + 0.08x |
||
|
D. y = 255 - 0.08x |
Predict the owl population in North America for the year 2014 if there were 280 in 2008 and 255 in 2010.
|
A. 230 |
||
|
B. 355 |
||
|
C. 330 |
||
|
D. 205 |
You just got a new job in retail and you are given two options for your earnings:
Option 1: Base salary of $15,000 per year plus a commission of 14% of your sales.
Option 2: Base salary of $18,000 per year plus a commission of 10% of your sales.
How much money in sales would you need to make in order for Option 1 to yield a higher income than Option 2?
|
A. More than $12,500 |
||
|
B. More than $137,500 |
||
|
C. More than $75,000 |
||
|
D. More than $18,000 |
A regression was run to determine if there is a relationship between how many hours of TV a person watches in a month (x) and the number of pizzas a person eats (y). Use a graphing calculator to graph this regression and predict how many pizzas a person who watches 30 hours of TV per month eats.
y = ax + b
a = -1.2
b = 38.7
|
A. Less than one pizza |
||
|
B. Between two and three pizzas per month |
||
|
C. Four pizzas |
||
|
D. More than four pizzas |
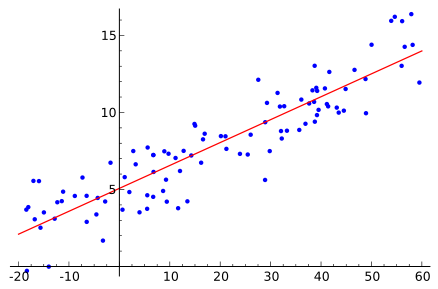
|
A. -0.957 |
||
|
B. 0.235 |
||
|
C. -0.235 |
||
|
D. 0.869 |
Given the table below which represents the dollars (in millions) of Brand X candies sold per year, determine if the trend appears linear. If so, use a graphing calculator to determine what year the dollars of candies sold will reach 3.4 million.
| Year | 1996 | 1998 | 2000 | 2002 | 2004 | 2006 | 2008 | 2010 | 2012 |
| $$ | 1.2 | 1.5 | 1.6 | 1.9 | 2.1 | 2.4 | 2.5 | 2.8 | 3.1 |
|
A. 2015 |
||
|
B. 2013 |
||
|
C. 2018 |
||
|
D. Not linear |
Given the table below, which represents the dollars (in millions) of Brand X candies sold per year, determine if the trend appears linear. If so, use a graphing calculator to determine the correlation coefficient for this regression.
| Year | 1996 | 1998 | 2000 | 2002 | 2004 | 2006 | 2008 | 2010 | 2012 |
| $$ | 1.2 | 1.5 | 1.6 | 1.9 | 2.1 | 2.4 | 2.5 | 2.8 | 3.1 |
|
A. 0.876 |
||
|
B. 0.996 |
||
|
C. -0.993 |
||
|
D. Not linear |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. No solution |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Write an equation for the following transformation of the graph below.
- Move 3 units to the right
- Move down 2 units
- Vertical stretch such that the graph passes through the point (1,2)
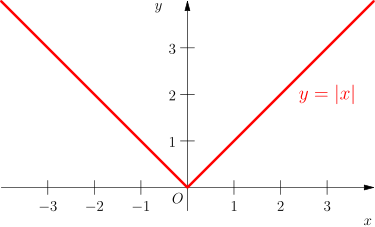
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. x = 5, -5 |
||
|
B. x = 3, -7 |
||
|
C. x = -3, 7 |
||
|
D. No horizontal intercepts |
The math grades for two students are listed below over the given time span. Which student's grade increased at a higher rate?
| Year | Bobby | Fred |
| 2009 | 75 | 69 |
| 2012 | 89 | 84 |
|
A. They increased at the same rate. |
||
|
B. More information is needed to solve this. |
||
|
C. Bobby |
||
|
D. Fred |
|
A. y = 2x + 3 |
||
|
B. y = 0.66x + 6 |
||
|
C. y = -6x+ 1.5 |
||
|
D. y = -1.5x + 6 |
|
A. 3 - 30w |
||
|
B. 30 - 3w |
||
|
C. 3 = 30w |
||
|
D. 3w - 30 |
|
A. (1.5, 2.5) |
||
|
B. (0.5, 3.5) |
||
|
C. (3, 7) |
||
|
D. (1.7, 2.1) |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. Vertical intercept: x=2,-1, or 4; horizontal intercept: y=8 |
||
|
B. Vertical intercept: y=0; horizontal intercept: x=2, or -1 |
||
|
C. Vertical intercept: y=8; horizontal intercept: x=2,-1, or 4 |
||
|
D. Vertical intercept: x=2, or -1; horizontal intercept: y=8 |
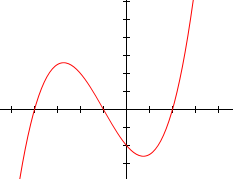
Determine the number of turning points for the following graph.
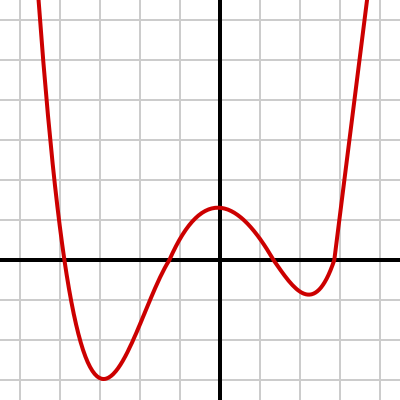
|
A. 1 |
||
|
B. 2 |
||
|
C. 3 |
||
|
D. 4 |
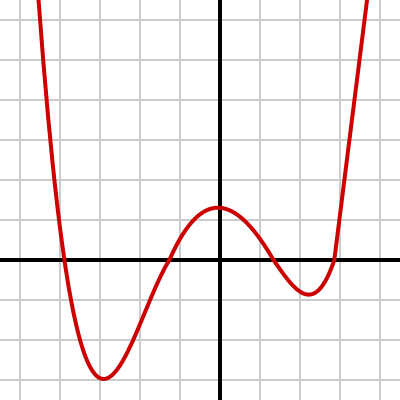
What can you conclude about the degree of the polynomal graphed below?

|
A. Even, degree of 2 |
||
|
B. Odd, degree of 3 |
||
|
C. Odd, degree of 5 or more |
||
|
D. Even, degree of 4 or more |
What can you conclude about the long run behavior of the polynomal graphed below?

|
A. As |
||
|
B. As |
||
|
C. As |
||
|
D. As |
|
A. x = -0.477 |
||
|
B. x = 10.477 |
||
|
C. x = 0.477, -10.477 |
||
|
D. x = -0.477, 10.477 |
|
A. Impossible to calculate |
||
|
B. After -1.001 seconds |
||
|
C. After 27.3 seconds |
||
|
D. After 1.001 seconds |
|
A. t = -0.325, 12.325 |
||
|
B. t = 0.325, -12.325 |
||
|
C. t = 0, 3 |
||
|
D. t = -1.325, 3.325 |
|
A. Impossible to calculate |
||
|
B. After 0.989 seconds |
||
|
C. After -0.989 seconds |
||
|
D. After 28.655 seconds |
Find the equation for the graph below (assume a scale of 1 unit).
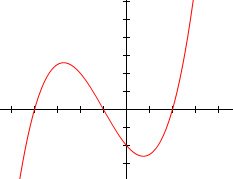
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |

|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. Minimum: (0, -8); maximum: (-1, 0) |
||
|
B. Minimum: (-2, 0); maximum: (0.67, -9.48) |
||
|
C. Minimum: (0.67, -9.48); maximum: (-2, 0) |
||
|
D. Minimum: (0, 0); maximum: (-1, 1) |
|
A. x = -3, 3 each with multiplicity of 2 |
||
|
B. x = -3, -5 each with multiplicity of 1 |
||
|
C. x = -5, 3 each with multiplicity of 2 |
||
|
D. x = -3, -5, 3 each with multiplicity of 1 |
|
A. (-0.91, -6.47) and (-2, 0) |
||
|
B. (0.42, -0.57) and (2.55, 6.94) |
||
|
C. (-0.91, -6.47) and (2.55, 6.94) |
||
|
D. (0.42, -0.57) and (-2, 0) |
|
A. x = 1, -3 |
||
|
B. x = -1, 3 |
||
|
C. x = 0, -3 |
||
|
D. x = 2, 3 |
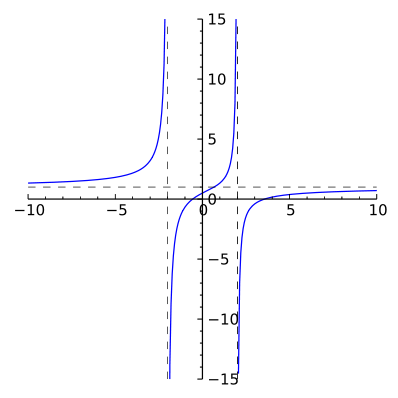
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |

|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. w(t)=4t+1 |
||
|
B. w(t)=75+7t |
||
|
C. w(t)=75t+7 |
||
|
D. w(t)=79t+8 |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
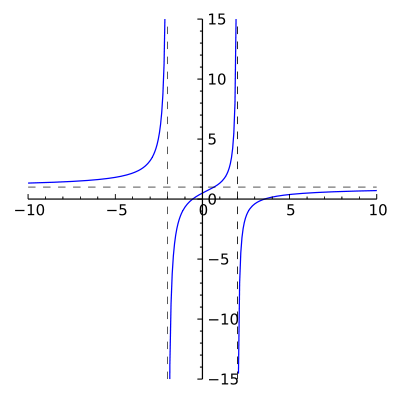
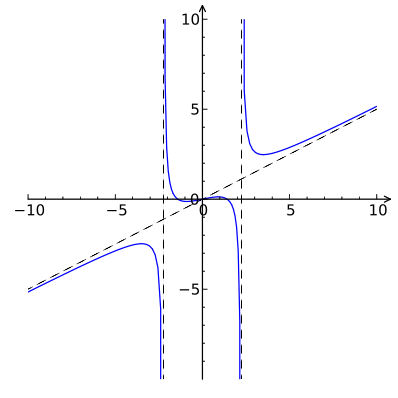
Sketch a graph of the following equation ![]() and determine which graph below represents this function.
and determine which graph below represents this function.
Graph A
Graph B
Graph C
Graph D
|
A. Graph A |
||
|
B. Graph B |
||
|
C. Graph C |
||
|
D. Graph D |
|
A. 1 |
||
|
B. 2 |
||
|
C. 3 |
||
|
D. 4 |
|
A. 1 |
||
|
B. 2 |
||
|
C. 3 |
||
|
D. 4 |
Sketch a graph of the following equation ![]() and determine which graph below represents this function.
and determine which graph below represents this function.
Graph A

Graph B

Graph C

Graph D

|
A. Graph A |
||
|
B. Graph B |
||
|
C. Graph C |
||
|
D. Graph D |
A jewelry store has a stock of 100 necklaces. It is selling 5% of its necklaces each week (w). Write an equation demonstrating this decay.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
A jewelry store has a stock of 100 necklaces. It is selling 5% of its necklaces each week (w). Approximately how many necklaces will it have left after 12 weeks?
|
A. 85 |
||
|
B. None |
||
|
C. 2 |
||
|
D. 54 |
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Determine the equation for the blue function in the graph below.
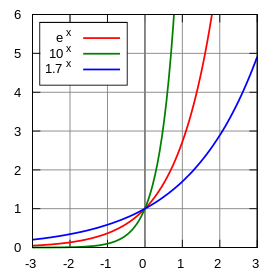
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Sketch a graph of the function ![]() and determine which function in the graph below represents it (assume a scale of 1).
and determine which function in the graph below represents it (assume a scale of 1).
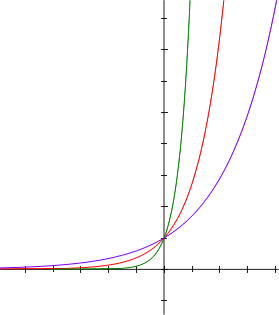
|
A. Green |
||
|
B. Red |
||
|
C. Purple |
||
|
D. None of these |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. $5,190.70 |
||
|
B. $414,517.29 |
||
|
C. $5,229.70 |
||
|
D. $7,834.96 |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Use the exponent property for logs to rewrite ![]()
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. x = -8.53 |
||
|
B. x = -0.117 |
||
|
C. x = -23.82 |
||
|
D. x = -15.29 |
|
A. 5% per 6 months |
||
|
B. .05% per month |
||
|
C. .05% per 6 months |
||
|
D. 5% per month |
Use the sum and difference properties of logs to write ![]() as a single logarithm.
as a single logarithm.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. 2 |
||
|
B. 54 |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
|
A. As |
||
|
B. As |
||
|
C. As |
||
|
D. As |
|
A. 1 day |
||
|
B. 2 days |
||
|
C. 3 days |
||
|
D. 4 days |
|
A. 96.6% |
||
|
B. 3.4% |
||
|
C. 50% |
||
|
D. 0.034% |
|
A. Less than a month |
||
|
B. 6 months |
||
|
C. 7.3 months |
||
|
D. 1.1 months |
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
The table below represents the dollars (in millions) of Brand X candies sold per year. Use technology to fit an exponential function to this data using linearization. Then determine the percentage increase per year.
| Year | 1996 | 1998 | 2000 | 2002 | 2004 | 2006 | 2008 | ||
| $$ | 1.2 | 1.5 | 1.6 | 1.9 | 2.1 | 2.4 | 2.5 |
|
A. 6.3% |
||
|
B. 2.6% |
||
|
C. 52.7% |
||
|
D. 5.3% |
Complete the table below for the function ![]() on a semilog graph with a logarithmic scale on the vertical axis.
on a semilog graph with a logarithmic scale on the vertical axis.
| x | log (f(x)) |
| -2 | |
| -1 | |
| 0 | |
| 1 | |
| 2 |
|
A. 1, 2, 4, 16, 32 |
||
|
B. -2, -1, 0, 1, 2 |
||
|
C. -0.6, -0.3, 0, 0.3, 0.6 |
||
|
D. 0, 0.3, 0.6, 1.2, 1.5 |
Determine which function below represents ![]()
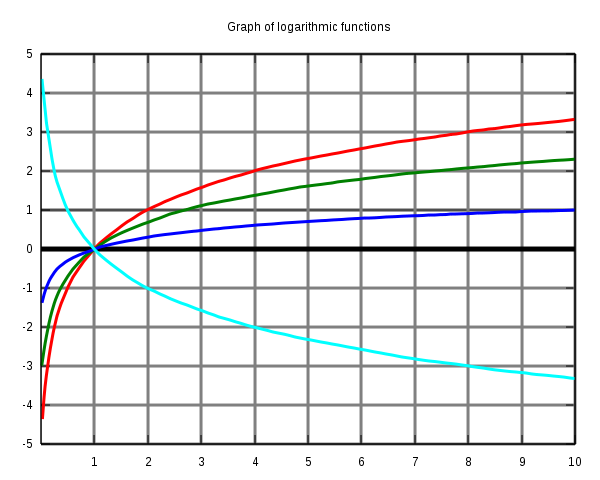
|
A. Red |
||
|
B. Green |
||
|
C. Blue |
||
|
D. Cyan |