1
A boat heads north at 40 miles per hour, and the wind blows east at 30 miles per hour (mph). What is the speed of the boat?
Choose one answer.
| a. 10 mph | ||
| b. 30 mph | ||
| c. 40 mph | ||
| d. 50 mph |
Question
2
A boat heads north at 40 miles per hour, and the wind blows east at 30 miles per hour. What is the direction of the boat?
Choose one answer.
| a. 53° | ||
| b. 45° | ||
| c. 90° | ||
| d. None of the above |
Question
3
Choose the best answer to fill in the blanks. If 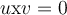 ,
then
,
then 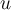 and
and 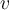 are _____________ vectors, and if
are _____________ vectors, and if 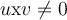 , then
, then 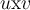 is _____________ to both
is _____________ to both 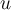 and
and 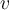 .
.
Choose one answer.
| a. Non-zero, equal | ||
| b. Orthogonal, parallel | ||
| c. Parallel, orthogonal | ||
| d. Zero, orthogonal |
Question
4
Choose the best answer to fill in the blanks. The __________ of the unit tangent vector remains constant; therefore, as a particle moves, the only thing
that changes is the ___________ of T.
Choose one answer.
| a. length, magnitude | ||
| b. direction, magnitude | ||
| c. length, direction | ||
| d. magnitude, length |
Question
5
Convert the vector 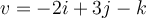 to component form.
to component form.
Choose one answer.
| a. <-2,2> | ||
| b. <2,-3,1> | ||
| c. <-2,3,-1> | ||
| d. <2,3,-1> |
Question
6
Evaluate L' (t), if L(t)= r(t)×v(t), where r(t) and v(t) are both vector-valued functions and r' (t)=v(t) and r'' (t)=a(t).
Choose one answer.
| a. L'(t) = v(t) ⋅ v(t) + r(t) × v(t) | ||
| b. L'(t) = v(t) ⋅ v(t) | ||
| c. L'(t) = r(t) × a(t) | ||
| d. L'(t) = v(t) ⋅ v(t) + r(t) × a(t) |
Question
7
Evaluate the length of the curve r(t)= < t, sin(2t), cos(2t) > on the interval 0 ≤ t ≤ 2π.
Choose one answer.
| a. √2 | ||
| b. 2√5 | ||
| c. 5π√2 | ||
| d. 2π√5 |
Question
8
Fill in the blank. Suppose v(t) is a vector such that ‖v(t)‖=c for all t, then v'(t) is ___________ to v(t).
Choose one answer.
| a. equal | ||
| b. orthogonal | ||
| c. anti-derivative | ||
| d. parallel |
Question
9
Fill in the blank. The speed of an object is the ____________ of the velocity vector.
Choose one answer.
| a. distance | ||
| b. magnitude | ||
| c. derivative | ||
| d. anti-derivative |
Question
10
Find  X
X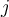 .
.
Choose one answer.
| a. 0 | ||
|
b. - |
||
|
c. |
||
| d. None of the above |
Question
11
Find the acceleration of the following function x(t) = <t3,t2,t2>.
Choose one answer.
| a. <6t, 2, 2> | ||
| b. <3t, 2t, 2t> | ||
| c. <6t, 0, 0> | ||
| d. None of the above |
Question
12
Find the angle in degrees between vectors 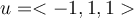 and
and
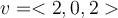 .
.
Choose one answer.
| a. 0° | ||
| b. 90° | ||
| c. 180° | ||
| d. 45° |
Question
13
Find the arc length function for the curve given by r(t)= <sin(3t),cos(3t)>.
Choose one answer.
| a. 3t | ||
| b. 9t | ||
| c. 3 | ||
| d. All of the above |
Question
14
Find the curvature k for the curve given by 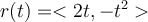 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
15
Find the equation of the plane through the point ( 0,0,0), ( 1,2,0), and ( 2,1,0).
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
16
Find the linear acceleration for the curve given by r(t)= < cost, sint >.
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. k | ||
| d. None of the above |
Question
17
Find the unit normal N(t) for the curve given by
r(t)= <-2t,-t2>.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
18
Find the unit tangent vector to the curve 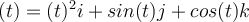 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
19
Find the velocity of the following function x(t) = <t3,t2,t2>
Choose one answer.
| a. <3t2,1,2t> | ||
| b. <3t, 0, 2> | ||
| c. <3t2,t,t> | ||
| d. <3t2,2t,2t> |
Question
20
Let 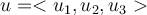 and
and 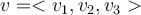 be vectors, then what is
be vectors, then what is  ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. None of the above |
Question
21
Suppose a car brakes and decelerates at a constant rate of 10 ft/s2. Suppose it takes the car 100 ft before coming to a stop. How fast was the
car traveling when the driver applied the brakes?
Choose one answer.
| a. 10 ft/s | ||
| b. 44.72 ft/s2 | ||
| c. 44.72 ft/s | ||
| d. 10.25 ft/s |
Question
22
The curvature of a circle is equal to which of the following?
Choose one answer.
| a. 0 | ||
| b. The reciprocal of its radius | ||
| c. Its radius | ||
| d. None of the above |
Question
23
What is the standard parameterization of a circle with radius 1 and center (0, 2)?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
24
What is the velocity v(2) at the point of tangency to r(t)=
<2t2,t3>?
Choose one answer.
| a. <8, 8> | ||
| b. <8, 12> | ||
| c. <12, 8> | ||
| d. <2, 2> |
Question
25
Find the vector 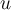 with initial point P1 (-1,-3) and final point P2 (0,2).
with initial point P1 (-1,-3) and final point P2 (0,2).
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
26
Determine where the function 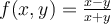 is continuous?
is continuous?
Choose one answer.
| a. Continuous for x≠-y | ||
| b. Continuous for x≠y | ||
| c. Not a continuous function | ||
| d. None of the above |
Question
27
Evaluate df⁄dt given that f(x,y)=
x2+y2 and x(t)= t5,y(t)=2 cos(t).
Choose one answer.
| a. 10t9-8cos(t)sin(t) | ||
| b. 10t4-4ysin(t) | ||
| c. 2t5+4cos(t) | ||
| d. None of the above |
Question
28
Evaluate 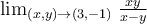 .
.
Choose one answer.
| a. ¾ | ||
| b. -¾ | ||
| c. -1 | ||
| d. Undefined |
Question
29
Fill in the blank. A function 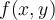 is _________ at the
point
is _________ at the
point 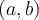 , if
, if 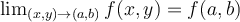 .
.
Choose one answer.
| a. defined | ||
| b. undefined | ||
| c. continuous | ||
| d. differentiable |
Question
30
Fill in the blank. The domain of the function 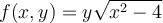 is
__________.
is
__________.
Choose one answer.
| a. not connected | ||
| b. undefined | ||
| c. dom(f)={(x,y)|x≠4} | ||
| d. connected |
Question
31
Fill in the blank. The domain of the function 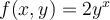 is
____________.
is
____________.
Choose one answer.
| a. closed and unbounded | ||
| b. connected and bounded | ||
| c. open, connected, and unbounded | ||
| d. closed, connected, and bounded |
Question
32
Find 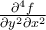 of
of 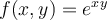 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
33
Find each of the directional derivatives of f(x,y)= x cos(y) in the direction of v = <1,2>?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
34
Find fx (x,y), if f(x,y) = y sin(x).
Choose one answer.
| a. fx(x,y) = cos(x) | ||
| b. fx(x,y) = -cos(x) | ||
| c. fx(x,y) = y cos(x) | ||
| d. fx(x,y) = y cos(-x) |
Question
35
Find fxx (x,y), if f(x,y) = 2x3 + x2y5.
Choose one answer.
| a. fxx(x,y) = 6x+y5 | ||
| b. fxx(x,y) = 6+10y3 | ||
| c. fxx(x,y) = 12x+2y5 | ||
| d. None of the above |
Question
36
Find 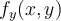 , if
, if 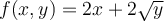 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
37
Find fyx(x,y), if f(x,y) = x sin(y).
Choose one answer.
| a. fyx(x,y) = cos(y) | ||
| b. fyx(x,y) = xcos(y) | ||
| c. fyx(x,y) = -cos(y) | ||
| d. fyx(x,y) = -xcos(y) |
Question
38
Find the domain of 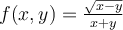 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
39
Suppose f and g are continuous at point (a, b), then which of the following functions is also continuous?
Choose one answer.
| a. f/g | ||
| b. f + g | ||
| c. f - g | ||
| d. All of the above |
Question
40
Suppose that A(x,t) and B(x,t) are both solutions to the heat equation, then which of the following is also a solution?
Choose one answer.
| a. cA(x,t), for a constant c | ||
| b. cB(x,t), for a constant c | ||
| c. αA(x,t)+ βB(x,t), for constants α,β | ||
| d. All of the above |
Question
41
The directional derivative, given by 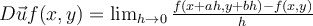 , provides
which of the following?
, provides
which of the following?
Choose one answer.
| a. The rate of change of the unit vector u=<a,b> in a given direction | ||
| b. The rate of change of ‖f(x,y)‖ in the direction of a vector | ||
| c. The rate of change of f(x,y) in the direction of the unit vector u=<a,b> | ||
| d. None of the above |
Question
42
Use Lagrange Multipliers to find the maximum of f(x,y) = 4xy subject to the constraint x2+y2=1.
Choose one answer.
| a. Maximum value of 0 occurs at (0,0). | ||
|
b. Maximum value of 2 occurs at ± |
||
|
c. Maximum value of 2 occurs at |
||
| d. None of the above |
Question
43
What are boundary conditions?
Choose one answer.
| a. Constraints on the solutions at different points in space | ||
| b. Constraints indicating that the rate of change of a function must be along a normal vector | ||
| c. Conditions that hold for surfaces without boundaries | ||
| d. None of the above |
Question
44
What do the partial derivatives represent?
Choose one answer.
| a. The rates of change of the functions as the variables change | ||
| b. The change in the magnitude of the function | ||
| c. The points at which the value of the function is zero | ||
| d. None of the above |
Question
45
What is 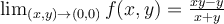 ?
?
Choose one answer.
| a. Does not exist | ||
| b. 0 | ||
| c. -1 | ||
| d. x = 0 |
Question
46
What is the definition of the partial derivative of f(x,y) with respect to x?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
47
What is the domain of the function 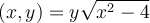 ?
?
Choose one answer.
| a. Connected | ||
| b. ℝ | ||
| c. ℝ - {0, 0} | ||
| d. None of the above |
Question
48
What is the general solution to the differential equationy''+k2 y=0?
Choose one answer.
| a. y(t)= A cos(kt)+ B sin(kt) | ||
| b. y(t)=Aekt | ||
| c. y(t)=A cosh(kt)+ B sinh(kt) | ||
| d. None of the above |
Question
49
Which of the following statements is true of f(x,y) = x cos(y)?
Choose one answer.
| a. fxx = fyy | ||
| b. fxy = fyx | ||
| c. fxy = -fyx | ||
| d. All of the above |
Question
50
Which of the following statements is true of f(x,y)= x+y?
Choose one answer.
| a. fxx = fyy | ||
| b. fxy = fyx | ||
| c. fxy = -fyx | ||
| d. All of the above |
Question
51
Find the domain of 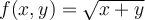 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
52
Calculate the divergence of 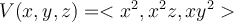 .
.
Choose one answer.
| a. 2x + 2y + 2z | ||
| b. 2x + yz | ||
| c. xyz | ||
| d. 2x |
Question
53
Choose the best answers to fill in the blanks. If 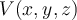 is the gradient of some function
is the gradient of some function 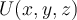 , then
, then 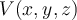 is called a _____________, and function
is called a _____________, and function 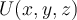 is said to be a ______________ for
is said to be a ______________ for 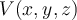 .
.
Choose one answer.
| a. tangent vector field, conservative vector field | ||
| b. conservative vector field, potential | ||
| c. potential, conservative vector field | ||
| d. conservative vector field, tangent vector field |
Question
54
Compute the following integral: 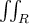
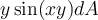 on
on 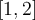 ×
× 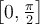 .
.
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. π | ||
| d. None of the above |
Question
55
Evaluate 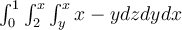 .
.
Choose one answer.
| a. (-5)/4 | ||
| b. 4/5 | ||
| c. 0 | ||
| d. -1 |
Question
56
Evaluate 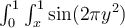
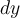
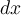 .
.
Choose one answer.
| a. 1/2π | ||
| b. (-1)/2π | ||
| c. 1 | ||
| d. 0 |
Question
57
Evaluate 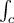
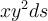 , where C is the right half of the circle parameterized by x=3
cos(t),y=3 sin(t) for t in
, where C is the right half of the circle parameterized by x=3
cos(t),y=3 sin(t) for t in 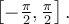
Choose one answer.
| a. 27 | ||
| b. 54 | ||
| c. 50 | ||
| d. 81 |
Question
58
Fill in the blank. The vector field 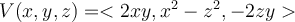 is
___________.
is
___________.
Choose one answer.
| a. conservative | ||
| b. constant | ||
| c. not a vector field | ||
| d. undefined |
Question
59
Find the center of mass of the lamina of the unit square with mass density m(x,y)=(x+y) kg/m2.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
60
Find the gradient vector field of U(x,y)= -x2-y2.
Choose one answer.
| a. U= <-2x,-2y> | ||
| b. U= <2x,2y> | ||
| c. U= <-x,-y> | ||
| d. U= <x+y,x-y> |
Question
61
Find the volume of a solid between z=x and z=x-y over R: y = 0 and y = 1 and x = y3 and x = y.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
62
Find the volume of a solid S that is bounded by x2+y2+ z=16, the planes x=2 and y=2, and the three coordinate planes.
Choose one answer.
| a. 160 | ||
|
b. |
||
|
c. |
||
| d. 64 |
Question
63
Fubini's theorem does NOT apply to 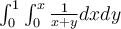 because of
which reason?
because of
which reason?
Choose one answer.
| a. The function is not bounded on [0,1]x[0,1]. | ||
| b. The function is bounded on [0,1]x[0,1]. | ||
| c. The function is continuous on all points. | ||
| d. The function is a constant. |
Question
64
Fubini's theorem states that if a function f(x, y) is continuous on the rectangle R = [a, b] x [c, d], then which of the following is true?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. All of the above |
Question
65
If 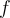 is a constant function
is a constant function 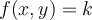 , and
, and 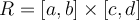 , then
, then 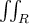
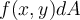 = _________.
= _________.
Choose one answer.
| a. k | ||
| b. k((b - a) +(d - c)) | ||
| c. k(b - a)(d - c) | ||
| d. 0 |
Question
66
Use Green's theorem to evaluate 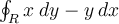 , where R is a unit
square.
, where R is a unit
square.
Choose one answer.
| a. -1 | ||
| b. 0 | ||
| c. 1 | ||
| d. 2 |
Question
67
Use Green's theorem to find the area of a disk of radius 2.
Choose one answer.
| a. 2π | ||
| b. 8π | ||
| c. 4π | ||
| d. π |
Question
68
Use the properties of the double integrals 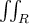
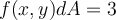 and
and 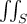
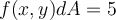 to evaluate
to evaluate 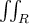
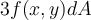 .
.
Choose one answer.
| a. 2 | ||
| b. 9 | ||
| c. 10 | ||
| d. 15 |
Question
69
Using Fubini's theorem, calculate 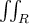
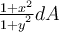 , where R = [0, 1] x [0, 1].
, where R = [0, 1] x [0, 1].
Choose one answer.
|
a. |
||
|
b. 2 |
||
|
c. |
||
|
d. |
Question
70
What is the line integral of a vector field V along a curve C?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
71
What is the mass of the lamina of the unit square with a height of 1 and a mass density of m(x, y) = (x + y) kg/m2.
Choose one answer.
| a. 1 kg | ||
| b. 2 kg | ||
| c. 3 kg | ||
| d. 4 kg |
Question
72
What type of an integral is this: 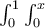
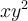
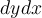
Choose one answer.
| a. Undefined | ||
| b. Type II | ||
| c. Type I | ||
| d. None of the above |
Question
73
Which of the following describes the image of [0, 1] x [0, 2π] under the transformation T(u,v)= <2u cos(v),2u sin(v)>?
Choose one answer.
| a. Cube | ||
| b. Sphere | ||
| c. Ellipse | ||
| d. None of the above |
Question
74
Which of the following is a Type I integral?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. None of the above |
Question
75
Which of the following is a Type II integral?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. All of the above |
Question
76
Which of the following statements is false?
Choose one answer.
| a. If f(x,y,z) has a continuous second or partial derivative, then curl(∇f)= 0. | ||
|
b. If |
||
|
c. If |
||
|
d. |
Question
77
Compute the following integral: 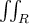
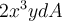 on
on 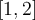 ×
× 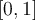 .
.
Choose one answer.
| a. 60 | ||
| b. 64 | ||
| c. 32 | ||
| d. 16 |
Question
78
Apply Stokes' theorem to evaluate the appropriate integral. Let S be the hemisphere x2+y2+z2=16, and let z ≥0 and F = <
x,x,y>.
Choose one answer.
| a. 4π | ||
| b. 8π | ||
| c. 16π | ||
| d. 64π |
Question
79
Apply Stokes' theorem to evaluate the appropriate integral. Let C be the circle of radius R centered at the origin, and let F = -y3
i+x3j be the vector field.
Choose one answer.
| a. π/2 R4 | ||
| b. π/3 R3 | ||
| c. 3π/4 R4 | ||
| d. 3π/2 R4 |
Question
80
Calculate the flux of F over S, where F is the vector field and S is the boundary of the region enclosed by the paraboloid
z=1-x2-y2 and the plane z=0.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
81
Calculate the flux of F(x,y,z) = <x,y,-2z> over the unit sphere.
Choose one answer.
| a. 0 | ||
|
b. |
||
|
c. |
||
| d. None of the above |
Question
82
Calculate the flux of a vector field F = over S, where S is the boundary of the unit sphere.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
83
Calculate the surface area of sphere of radius R.
Choose one answer.
| a. πR2 | ||
| b. 4πR2 | ||
| c. 4R2 | ||
| d. 4π |
Question
84
Calculate the surface area of the part xy + z that is in the plane x + y + z = 2 in the first octant.
Choose one answer.
| a. 2√3 | ||
| b. √3 | ||
| c. 4√3 | ||
| d. 2 |
Question
85
Compute the flux of the vector field 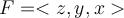 through the
unit sphere
through the
unit sphere 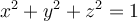 .
.
Choose one answer.
|
a. |
||
|
b. |
||
| c. 0 | ||
| d. 1 |
Question
86
Evaluate 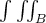
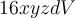 over B = [1, 3] x [0, 1] x [0, 2].
over B = [1, 3] x [0, 1] x [0, 2].
Choose one answer.
| a. 16 | ||
| b. 32 | ||
| c. 48 | ||
| d. 64 |
Question
87
Fill in the blank. If div(V)=0, then there exists a vector field W such that _______________.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
88
Given the mass density, m(x,y,z)=3-z2 over B = [0, 1] x [0, 1] x [0, 1], find the mass of the solid.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. 1 |
Question
89
If F(x,y,z) and G(x,y,z) are differentiable in each component, then which of the following is true?
Choose one answer.
| a. F'(x,y,z) = G'(x,y,z). | ||
| b. div(F(x,y,z)+ G(x,y,z)) = F'(x,y,z) + G'(x,y,z). | ||
| c. div(F(x,y,z)+ G(x,y,z))= div(F(x,y,z))+ div(G(x,y,z)). | ||
| d. All of the above |
Question
90
Let C be a simple closed curve and D be the region enclosed by C. Then, which of the following is true?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
91
If a solid has a mass density of m(x,y,z), then what is the total gravitational potential energy of the solid?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
92
Suppose a surface S is parameterized by (u,v)= <x(u,v),y(u,v),z(u,v)>, where (u, v) lies in a region R in the u-v plane. Then, we can rewrite
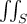
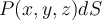 as which of the following?
as which of the following?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
93
Suppose a vector field F represents the velocity of a fluid through a membrane represented by S. What does the flux represent?
Choose one answer.
| a. The rate of change in direction | ||
| b. Surface area of S | ||
| c. The volume of fluid passing through S | ||
| d. None of the above |
Question
94
The divergence theorem relates which of the following?
Choose one answer.
| a. The flux of a vector field to the flow of the vector field inside the surface | ||
| b. The behavior of the vector field on the surface to its curvature | ||
| c. The flux of a vector field through a surface to the behavior of the vector field inside the surface | ||
| d. None of the above |
Question
95
The surface integral in Stokes' theorem does not change if which of the following occurs?
Choose one answer.
| a. The surface S is changed to any surface as long as the boundary of S is still the curve C. | ||
| b. The surface S is changed to any surface as long as the boundary of S still intersects the curve C. | ||
| c. The surface S is changed to a sphere. | ||
| d. None of the above |
Question
96
Use Gauss's Law to calculate the electric field of an infinite sheet with a uniform charge density σ.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
97
Use the Fundamental Theorem for line integrals to evaluate 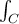 ∇f ∙
∇f ∙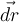 , where C is the top half of the circle
x2+y2=1, traversed counter clockwise, and f(x,y) =xy+x.
, where C is the top half of the circle
x2+y2=1, traversed counter clockwise, and f(x,y) =xy+x.
Choose one answer.
| a. -2 | ||
| b. 2 | ||
| c. 0 | ||
| d. None of the above |
Question
98
Using Fubini's theorem for double integrals, what can we say about Fubini's theorem for triple integrals?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
99
Using the divergence theorem, compute the flux of the vector field F(x,y,z)= <x,y,z> through the unit sphere.
Choose one answer.
| a. 3π | ||
| b. 4π | ||
| c. 8π | ||
| d. 16π |
Question
100
What is the definition of the surface area differential for a surface S?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
101
What is the volume of a solid between x = y and x =0, y = 0, y = 2, z = 0, and z = 1?
Choose one answer.
| a. 2 | ||
| b. 4 | ||
| c. 1 | ||
| d. 6 |