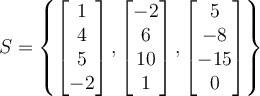
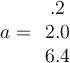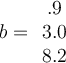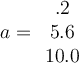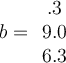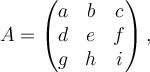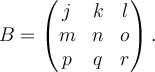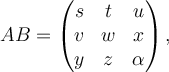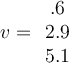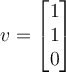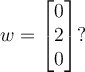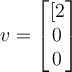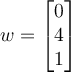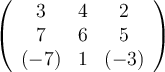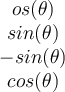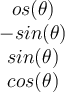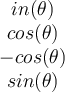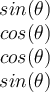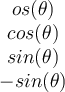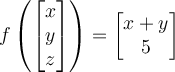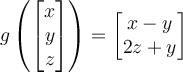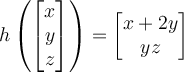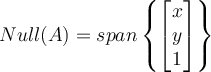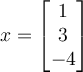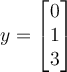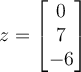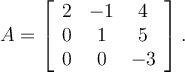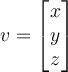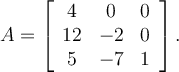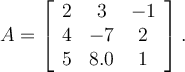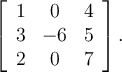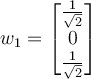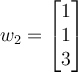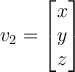If two vectors are orthogonal, then which of the following is true?
Choose one answer.
|
a. Their dot product is 0. |
||
|
b. Their cross product is 0. |
||
|
c. Their dot product is 1. |
||
|
d. Both A and B |
||
|
e. Both B and C |
Suppose 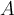 is matrix in
is matrix in 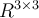 , and
, and 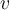 is a vector in
is a vector in 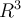 . Evaluate the following statement: there exists solution
. Evaluate the following statement: there exists solution 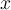 to the equation
to the equation 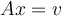 .
.
Choose one answer.
A system of linear equations with six unknowns can have how many solutions?
Choose one answer.
|
a. 0 |
||
|
b. 1 |
||
|
c. Infinitely many |
||
|
d. All of these answers |
||
|
e. None of these answers |
Similar matrices always have which of the following in common?
Choose one answer.
|
a. Column space |
||
|
b. Determinant |
||
|
c. Nullspace |
||
|
d. Eigenvectors |
||
|
e. Inverse |
Let 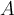 be a
be a 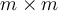 matrix. Let
matrix. Let 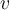 be a vector in the nullspace of
be a vector in the nullspace of 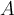 . Let
. Let 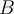 be another
be another 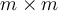 matrix. Evaluate the following statement:
matrix. Evaluate the following statement: 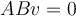 .
.
Choose one answer.
Two matrices are row-equivalent if and only if which of the following is true?
Choose one answer.
|
a. They have the same nullspace. |
||
|
b. They have the same eigenspace. |
||
|
c. One can be changed to the other by a sequence of elementary row operations. |
||
|
d. Both A and C |
||
|
e. Both B and C |
True or False: If A is a matrix and b is not the zero vector, then Ax = b has a solution if and only if b can be written as a linear combination of the columns of A.
Answer:
True
False
True or False: If A is a 12 x 15 matrix, the null-space of A must have dimension at least 1?
Answer:
True
False
If the rank of a 4 x 4 matrix is 3 then its determinant
Choose one answer.
|
a. =1 |
||
|
b. =0 |
||
|
c. cannot be determined |
If a 4 x 4 matrix is in row-echelon form the the entry in the third row, second column must be 0.
Answer:
True
False
True or False: A set of three non-zero vectors in the plane can be linearly independent.
Answer:
True
False
Suppose a matrix 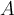 is a m x m matrix, which has characteristic polynomial
is a m x m matrix, which has characteristic polynomial 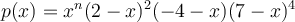 . Is
. Is 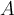 diagonalizable? Why, or why not?
diagonalizable? Why, or why not?
Choose one answer.
True or False: If two matrices have the same characteristic polynomial, then they are similar.
Answer:
True
False
If 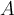 is a 4 x 4 real matrix which is true of the matrix
is a 4 x 4 real matrix which is true of the matrix 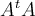
1. must have non-negative real eigenvalues
2. must have purely imaginary eigenvalues
3. must have an orthonormal basis of eigenvectors
4. is diagonalizable
1. must have non-negative real eigenvalues
2. must have purely imaginary eigenvalues
3. must have an orthonormal basis of eigenvectors
4. is diagonalizable
Choose one answer.
|
a. 1., 3. and 4. |
||
|
b. 2. and 3. |
||
|
c. 2., 3. and 4 |
||
|
d. 1. and 2. |
||
|
e. 1., 2., and 3. |
Which of the following is required of a set 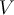 with a well-defined addition of elements and scalar multiplication over a field
with a well-defined addition of elements and scalar multiplication over a field 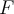 to be a vector space?
to be a vector space?
Choose one answer.
|
a. Every element of |
||
|
b. If |
||
|
c. |
||
|
d. All of the above |
||
|
e. A and B only |
Choose one answer.
If 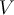 denotes the vector space of polynomials of degree at most 4 in one variable and
denotes the vector space of polynomials of degree at most 4 in one variable and 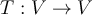 is the linear transformation defined by
is the linear transformation defined by
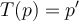 ,
,
where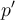 denotes the derivative of
denotes the derivative of 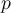 . If
. If 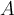 denotes the matrix representing
denotes the matrix representing 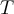 with respect to the basis
with respect to the basis 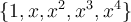 of
of 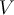 , then
, then
where
Choose one answer.
|
a. The determinant of |
||
|
b. |
||
|
c. The determinant of |
||
|
d. |
||
|
e. |
True or False: The vector space consisting of real numbers over the field of rational numbers has dimension 1.
Answer:
True
False
True or False: Two non-zero vectors can span a 3-dimensional vector space.
Answer:
True
False
True or False: Any set of 4 vectors in a 3-dimensional vector space must be linearly dependent.
Answer:
True
False