1
If two vectors are orthogonal, then which of the following is true?
Choose one answer.
| a. Their dot product is 0. | ||
| b. Their cross product is 0. | ||
| c. Their dot product is 1. | ||
| d. Both A and B | ||
| e. Both B and C |
Question
2
Let 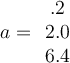 , and let
, and let 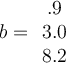 . What is
. What is 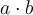 ?
?
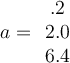 , and let
, and let 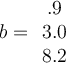 . What is
. What is
Answer:
Question
3
Let 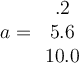 , and let
, and let 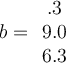 . If
. If 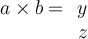 , what is
, what is 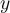 ?
?
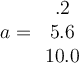 , and let
, and let 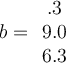 . If
. If
Answer:
Question
4
Let 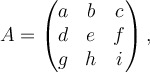
and let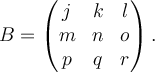
If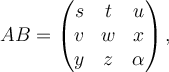
then what is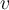 ?
?
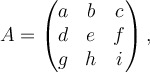
and let
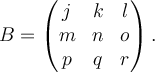
If
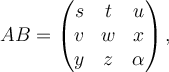
then what is
Answer:
Question
5
Let 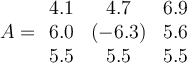 , and let
, and let 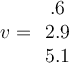 . If
. If 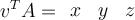 , then what is
, then what is 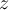 ?
?
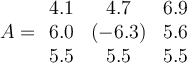 , and let
, and let 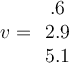 . If
. If
Answer:
Question
6
Consider this system: 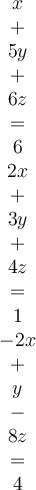 . What is
. What is 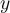 ?
?
Answer:
Question
7
Consider this system: 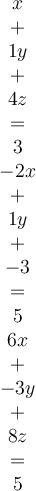 . What is
. What is 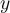 ?
?
Answer:
Question
8
Consider this system: 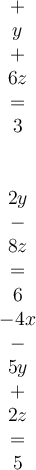 . What is
. What is 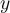 ?
?
Answer:
Question
9
Consider a parallelepiped  with three edges meeting
at a vertex at the origin, given these vectors:
with three edges meeting
at a vertex at the origin, given these vectors:  ,
,
 , and
, and  . What is its volume?
. What is its volume?
Answer:
Question
10
What is the angle (in radians) between the vectors
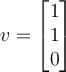
and
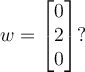
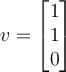
and
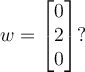
Answer:
Question
11
Find the length of the projection of the vector
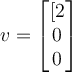
onto the vector
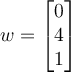 .
.
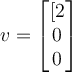
onto the vector
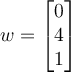 .
.
Answer:
Question
12
If 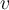 is a vector in the plane then the vector
is a vector in the plane then the vector
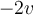
Choose one answer.
|
a. makes an angle of |
||
|
b. makes and angle of |
||
|
c. is perpendicular to |
||
|
d. makes an angle of |
Question
13
Calculate the determinant of this matrix: 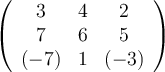 .
.
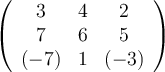 .
.
Answer:
Question
14
Suppose that  is a
is a 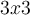 matrix and that
matrix and that 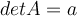 . Let
. Let 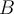 be an elementary matrix whose only action is to swap two rows of
be an elementary matrix whose only action is to swap two rows of
 . Let
. Let 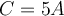 . What is
. What is 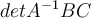 ?
?
Answer:
Question
15
Consider matrix  :
: 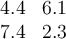 .
. 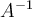 has this format:
has this format: 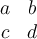 . What is the value of
. What is the value of 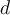 ?
?
Answer:
Question
16
Suppose  is matrix in
is matrix in 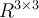 , and
, and 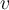 is a vector in
is a vector in  . Evaluate the following statement: there exists solution
. Evaluate the following statement: there exists solution 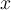 to the equation
to the equation 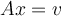 .
.
Choose one answer.
|
a. For this statement to be true, it is necessary that |
||
|
b. For this statement to be true, it is sufficient that |
||
|
c. For this statement to be true, it is necessary and sufficient that |
||
|
d. For this statement to be true, it is neither necessary nor sufficient that |
||
|
e. If |
Question
17
A system of linear equations with six unknowns can have how many solutions?
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. Infinitely many | ||
| d. All of these answers | ||
| e. None of these answers |
Question
18
Consider the linear map 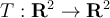 , which acts by rotating a
vector
, which acts by rotating a
vector 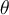 degrees counterclockwise around the origin.
Which of the following is the matrix of the linear transformation?
degrees counterclockwise around the origin.
Which of the following is the matrix of the linear transformation?
Choose one answer.
a. 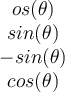
|
||
b. 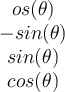
|
||
c. 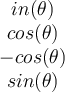
|
||
d. 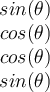
|
||
e. 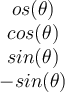
|
Question
19
Suppose that 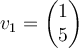
and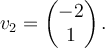
Consider the linear map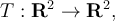
which satisfies
and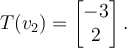
Let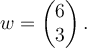
If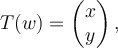
what is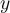 ?
?
and
Consider the linear map
which satisfies
and
Let
If
what is
Answer:
Question
20
Similar matrices always have which of the following in common?
Choose one answer.
| a. Column space | ||
| b. Determinant | ||
| c. Nullspace | ||
| d. Eigenvectors | ||
| e. Inverse |
Question
21
What is the dimension of the span of the set
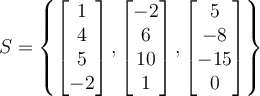

Answer:
Question
22
Suppose that the columns of an 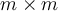 matrix
matrix  are linearly independent. Then, which of the following
statements is always true?
are linearly independent. Then, which of the following
statements is always true?
Choose one answer.
|
a. The kernel of |
||
|
b. The determinant of |
||
|
c. |
||
|
d. |
||
|
e. |
Question
23
Let  be a
be a 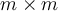 matrix. Let
matrix. Let  be a vector in the nullspace of
be a vector in the nullspace of  . Let
. Let  be another
be another 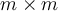 matrix. Evaluate the following statement:
matrix. Evaluate the following statement: 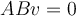 .
.
Choose one answer.
|
a. In order for this statement to be true, it is necessary that |
||
|
b. In order for this statement to be true, it is sufficient that |
||
|
c. In order for this statement to be true, it is necessary and sufficient that |
||
|
d. In order for this statement to be true, it is neither necessary nor sufficient that |
||
|
e. This statement is false if |
Question
24
Suppose that  is a
is a  matrix with determinant 2. What is
matrix with determinant 2. What is 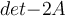 ?
?
Answer:
Question
25
Consider these maps from
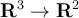
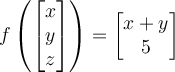
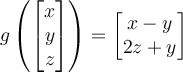
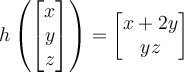 .
.
Which is linear?
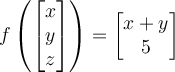
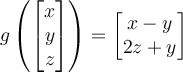
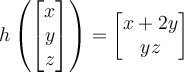 .
.Which is linear?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. All of these answers | ||
| e. None of these answers |
Question
26
Two matrices are row-equivalent if and only if which of the following is true?
Choose one answer.
| a. They have the same nullspace. | ||
| b. They have the same eigenspace. | ||
| c. One can be changed to the other by a sequence of elementary row operations. | ||
| d. Both A and C | ||
| e. Both B and C |
Question
27
Suppose a  matrix
matrix  is row-equivalent to the identity matrix. Which of the following may be
false?
is row-equivalent to the identity matrix. Which of the following may be
false?
Choose one answer.
|
a. |
||
|
b. The rowspace of |
||
|
c. The eigenvalues of |
||
|
d. The nullspace of |
||
|
e. |
Question
28
Consider the matrix 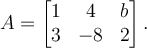
If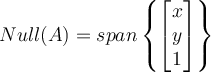
what is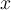 ?
?
If
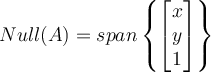
what is
Answer:
Question
29
True or False: If A is a matrix and b is not the zero vector, then Ax = b has a solution if and only if b can
be written as a linear combination of the columns of A.
Answer:
True False
Question
30
True or False: These vectors are linearly independent:
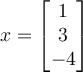
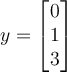
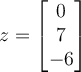
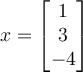
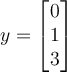
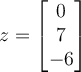
Answer:
True False
Question
31
Calculate the determinant of this matrix: 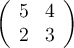 .
.
Answer:
Question
32
True or False: If A is a 12 x 15 matrix, the null-space of A must have dimension at least 1?
Answer:
True False
Question
33
Suppose that
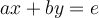 ,
,
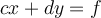
is a system of equations with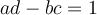 . The solution vector
is
. The solution vector
is
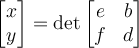
is a system of equations with
Answer:
True False
Question
34
If the rank of a 4 x 4 matrix is 3 then its determinant
Choose one answer.
| a. =1 | ||
| b. =0 | ||
| c. cannot be determined |
Question
35
If a 4 x 4 matrix is in row-echelon form the the entry in the third row, second column must be 0.
Answer:
True False
Question
36
True or False: A set of three non-zero vectors in the plane can be linearly independent.
Answer:
True False
Question
37
True or false: every non-vertical straight line in the plane is a subspace of 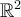 .
.
Answer:
True False
Question
38
If  is an n x n matrix of rank
is an n x n matrix of rank 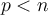 , then what is the dimension of the null-space of
, then what is the dimension of the null-space of  =?
=?
Choose one answer.
| a. p | ||
| b. n-p | ||
| c. n-p+1 | ||
| d. 0 | ||
| e. Cannot be determined from the data |
Question
39
True or False: To find an eigenvector of a matrix  corresponding to an eigenvalue
corresponding to an eigenvalue  of
of  , simply find any vector in the nullspace of
, simply find any vector in the nullspace of 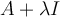 .
.
Answer:
True False
Question
40
Consider this matrix: 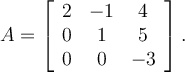
Clearly,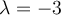 is an eigenvalue of
is an eigenvalue of  . Let
. Let
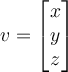
be the eigenvector corresponding to . If
. If
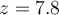 , what is
, what is 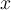 ?
?
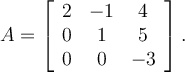
Clearly,
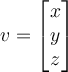
be the eigenvector corresponding to
Answer:
Question
41
Consider this matrix: 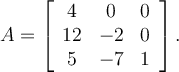
Clearly,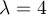 is an eigenvalue of
is an eigenvalue of  . Let
. Let
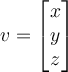
be the eigenvector corresponding to . If
. If
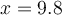 , what is
, what is 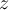 ?
?
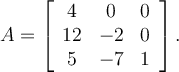
Clearly,
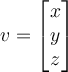
be the eigenvector corresponding to
Answer:
Question
42
Consider this matrix: 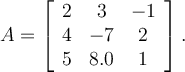
The characteristic polynomial of is of the form
is of the form
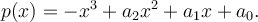
What is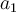 ?
?
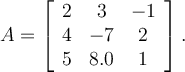
The characteristic polynomial of
What is
Answer:
Question
43
Suppose matrix  is an
is an 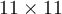 matrix with characteristic polynomial
matrix with characteristic polynomial 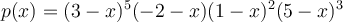 . What is the largest possible number of linearly independent solutions
to
. What is the largest possible number of linearly independent solutions
to 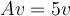 ?
?
Answer:
Question
44
Suppose a matrix  is a m x m
matrix, which has characteristic polynomial
is a m x m
matrix, which has characteristic polynomial 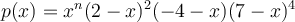 . Is
. Is
 diagonalizable? Why, or why not?
diagonalizable? Why, or why not?
Choose one answer.
|
a. No, because |
||
|
b. No, because |
||
|
c. Maybe, it depends on whether |
||
| d. Maybe, it depends on the dimensions of the eigenspaces. | ||
|
e. Yes, because all the roots of |
Question
45
Suppose a 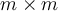 matrix
matrix  is diagonalizable. Then,
is diagonalizable. Then,  always has which of the following?
always has which of the following?
Choose one answer.
|
a. |
||
|
b. |
||
| c. Exactly as many linearly independent eigenvectors as eigenvalues | ||
|
d. |
||
|
e. |
Question
46
Consider this matrix:
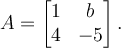
What is the largest eigenvalue of ?
?
What is the largest eigenvalue of
Answer:
Question
47
Compute the smallest (i.e., most negative) eigenvalue of this matrix: 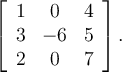
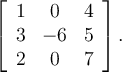
Answer:
Question
48
Suppose that 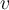 is an eigenvector of a matrix
is an eigenvector of a matrix
 corresponding to a nonzero eigenvalue
corresponding to a nonzero eigenvalue  . True or False:
. True or False: 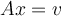 is always solvable.
is always solvable.
Answer:
True False
Question
49
True or False: If two matrices have the same characteristic polynomial, then they are similar.
Answer:
True False
Question
50
True or false: The polynomial 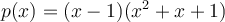 is the
characteristic polynomial of a symmetric matrix.
is the
characteristic polynomial of a symmetric matrix.
Answer:
True False
Question
51
Let 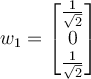
and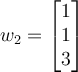
and
If is the orthonormal basis of
is the orthonormal basis of 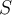 obtained by the Gram-Schmidt process with
obtained by the Gram-Schmidt process with
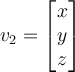
then
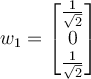
and
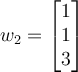
and
If
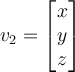
then
Choose one answer.
| a. 1 | ||
|
b. |
||
| c. 0 | ||
| d. -1 | ||
|
e. |
Question
52
True or false: the matrix
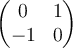
is orthogonal?
is orthogonal?
Answer:
True False
Question
53
If  is an
is an 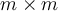 orthogonal matrix, which of the following may not be true about
orthogonal matrix, which of the following may not be true about
 .
.
Choose one answer.
|
a. The determinant of |
||
|
b. |
||
|
c. The rows of |
||
|
d. The columns of |
||
|
e. The nullity of |
Question
54
The line which gives the best least squares approximation to the points in the plane with coordinates 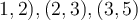 has slope
has slope
Choose one answer.
| a. 3/2 | ||
| b. 2/3 | ||
| c. -1/3 | ||
| d. 0 | ||
| e. 2 |
Question
55
Suppose A is a 3 x 3 symmetric matrix, 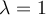 is
an eigenvalue of algebraic multiplicity 2 and
is
an eigenvalue of algebraic multiplicity 2 and 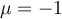 is an
eigenvalue of algebraic multiplicity 1. If
is an
eigenvalue of algebraic multiplicity 1. If

is an eigenvector corresponding to and
and

is an eigenvector corresponding to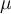 , then x=
, then x=
is an eigenvector corresponding to
is an eigenvector corresponding to
Answer:
Question
56
What is the geometric multiplicity of the eigenvalus 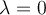 of the matrix
of the matrix
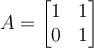 ?
?
Answer:
Question
57
What is the geometric multiplicity of the eigenvalue 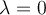 of the matrix
of the matrix
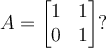
Answer:
Question
58
If  is a 4 x 4 real matrix then the matrix
is a 4 x 4 real matrix then the matrix
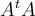
Choose one answer.
| a. is always symmetric | ||
| b. is always skew-symmetric | ||
| c. is always singular | ||
| d. is always non-singular |
Question
59
If  is a 4 x 4 real matrix which is true of the
matrix
is a 4 x 4 real matrix which is true of the
matrix 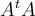
1. must have non-negative real eigenvalues
2. must have purely imaginary eigenvalues
3. must have an orthonormal basis of eigenvectors
4. is diagonalizable
1. must have non-negative real eigenvalues
2. must have purely imaginary eigenvalues
3. must have an orthonormal basis of eigenvectors
4. is diagonalizable
Choose one answer.
| a. 1., 3. and 4. | ||
| b. 2. and 3. | ||
| c. 2., 3. and 4 | ||
| d. 1. and 2. | ||
| e. 1., 2., and 3. |
Question
60
True or False: In a vector space of dimension 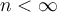 , any
spanning set of cardinality
, any
spanning set of cardinality 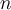 is a basis.
is a basis.
Answer:
True False
Question
61
Which of the following is required of a set 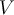 with a
well-defined addition of elements and scalar multiplication over a field
with a
well-defined addition of elements and scalar multiplication over a field 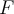 to be a vector space?
to be a vector space?
Choose one answer.
|
a. Every element of |
||
|
b. If |
||
|
c. |
||
| d. All of the above | ||
| e. A and B only |
Question
62
Consider 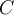 , which is the vector space of functions
that are continuous on the interval
, which is the vector space of functions
that are continuous on the interval 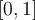 . Let
. Let
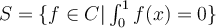 .
.
True or False: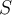 is a linear subspace of
is a linear subspace of 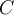 .
.
True or False:
Answer:
True False
Question
63
Consider a 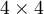 matrix
matrix  with eigenvalues
with eigenvalues 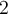 and
and 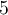 , each having multiplicity
, each having multiplicity 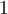
True or False: The set of all eigenvectors of form
a subspace of
form
a subspace of 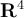 .
.
True or False: The set of all eigenvectors of
Answer:
True False
Question
64
Consider a 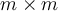 matrix
matrix  with eigenvalues -1, 4, and 5.
with eigenvalues -1, 4, and 5.
True or False: The set of all right eigenvectors of , which correspond to the eigenvector 4, form a subspace of
, which correspond to the eigenvector 4, form a subspace of 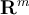 .
.
True or False: The set of all right eigenvectors of
Answer:
True False
Question
65
True or False: Trace is a linear operator on the vector space of  real-valued matrices endowed with the usual matrix addition and scalar multiplication.
real-valued matrices endowed with the usual matrix addition and scalar multiplication.
(Recall that for a matrix ,
, 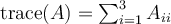 .)
.)
(Recall that for a matrix
Answer:
True False
Question
66
Suppose that 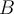 and
and 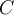 are bases for
are bases for 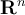 . Suppose that
. Suppose that 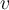 and
and 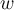 are orthogonal vectors in
are orthogonal vectors in 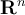 with coordinates corresponding to basis
with coordinates corresponding to basis 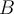 . Let
. Let 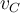 and
and 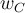 be the coordinate vectors for
be the coordinate vectors for 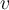 and
and 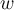 in the basis
in the basis 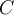 .
.
True or False: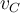 is orthogonal to
is orthogonal to 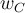 .
.
True or False:
Answer:
True False
Question
67
For any given real 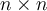 matrix
matrix  , evaluate the following statement:
, evaluate the following statement: 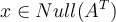 .
.
Choose one answer.
|
a. For this statement to be true, it is necessary that |
||
|
b. For this statement to be true, it is sufficient that |
||
|
c. For this statement to be true, it is necessary and sufficient that |
||
|
d. For this statement to be true, it is neither necessary nor sufficient that |
||
|
e. This statement is false if |
Question
68
If 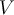 denotes the vector space of polynomials of
degree at most 4 in one variable and
denotes the vector space of polynomials of
degree at most 4 in one variable and 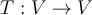 is the linear
transformation defined by
is the linear
transformation defined by
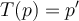 ,
,
where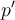 denotes the derivative of
denotes the derivative of 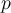 . If
. If  denotes the matrix representing
denotes the matrix representing 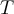 with respect to the basis
with respect to the basis 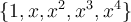 of
of 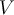 , then
, then
where
Choose one answer.
|
a. The determinant of |
||
|
b. |
||
|
c. The determinant of |
||
|
d. |
||
|
e. |
Question
69
If 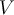 is the vector space of continuous function on
the interval
is the vector space of continuous function on
the interval 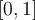 with inner product given by
with inner product given by
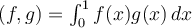 ,
,
find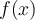 so that {
so that {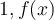 } is an orthonormal basis for the subspace spanned by {
} is an orthonormal basis for the subspace spanned by {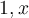 }.
}.
find
Answer:
Question
70
True or False: The vector space consisting of real numbers over the field of rational numbers has dimension 1.
Answer:
True False
Question
71
Let 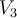 denote the vector space of polynomials of
degree at most 3 in one variable and
denote the vector space of polynomials of
degree at most 3 in one variable and  a collection
of distinct real numbers. If
a collection
of distinct real numbers. If 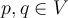 the function
the function
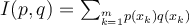 defines and inner product on
defines and inner product on 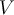 if
if
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. for any positive integer |
||
|
e. For no positive integer |
Question
72
If 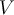 denotes the vector space of continuous functions
on the interval
denotes the vector space of continuous functions
on the interval 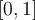 and for
and for 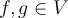 we define the function
we define the function 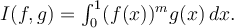 For which positive integers
For which positive integers 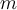 does
does 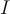 define an inner product on
define an inner product on 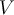 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. For all |
||
|
e. For no positive integer |
Question
73
If 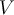 denotes the vector space of continuous functions
on the interval
denotes the vector space of continuous functions
on the interval 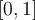 and
and  are distinct points in
are distinct points in 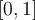 , for which values of the positive integer m is the
function
, for which values of the positive integer m is the
function
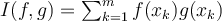
an inner product on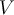 ?
?
an inner product on
Choose one answer.
|
a. |
||
|
b. |
||
|
c. all positive integers |
||
|
d. There is no |
Question
74
If 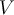 denotes the inner product space of continuous
functions on the interval
denotes the inner product space of continuous
functions on the interval  with inner product
defined as
with inner product
defined as 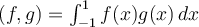 ,
,
the orthogonal projection of the function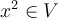 onto the
subspace spanned by
onto the
subspace spanned by 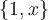 equals
equals
the orthogonal projection of the function
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
||
| e. None of the above |
Question
75
True or False: Two non-zero vectors can span a 3-dimensional vector space.
Answer:
True False
Question
76
True or False: Any set of 4 vectors in a 3-dimensional vector space must be linearly dependent.
Answer:
True False
Question
77
True or False: Any set of 4 vectors in a 3-dimensional vector space must be linearly dependent
Answer:
True False