1
Numerical differentiation formulas for a function f are typically found by doing which of the following?
Choose one answer.
| A. Finding a zero of f' | ||
| B. Approximating f by a polynomial P and differentiating P | ||
| C. Differentiating a Fourier transform of f and then applying an inverse transform | ||
| D. Finding the slope of f at two randomly generated points | ||
| E. None of the above |
Question
2
Let 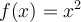 . Approximate
. Approximate 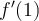 using the 2-point difference formula with
using the 2-point difference formula with 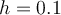 .
.
Choose one answer.
| A. 2.0 | ||
| B. 2.1 | ||
| C. 1.9 | ||
| D. 0.21 | ||
| E. 0.19 |
Question
3
For fixed 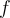 ,
, 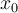 , and finite difference formula, there is an
, and finite difference formula, there is an 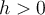 that minimizes the error in the computed approximation to
that minimizes the error in the computed approximation to 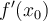 . Why?
. Why?
Choose one answer.
| A. Every difference formula has a truncation error formula that can be minimized. | ||
| B. High degree interpolating polynomials oscillate too much. | ||
|
C. Underflows increase as |
||
|
D. Overflows increase as |
||
|
E. Rounding errors increase as |
Question
4
Use a 3-point centered difference formula with 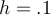 to
approximate
to
approximate 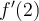 , where
, where
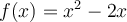 . Identify the best 4 significant digit approximate
below.
. Identify the best 4 significant digit approximate
below.
Choose one answer.
| A. 2.000 | ||
| B. 1.999 | ||
| C. 1.989 | ||
| D. 1.899 |
Question
5
If f(x) is only known at the uniformly spaced grid points 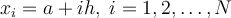 and a
and a 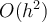 approximation to
approximation to 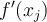 is desired at each
is desired at each 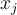 , then what combination of differentiation rules could be used?
, then what combination of differentiation rules could be used?
Choose one answer.
|
A. Centered difference formula at each |
||
| B. 3-point difference formulas, forward difference at left endpoint, backward difference at right endpoint, and centered difference elsewhere | ||
| C. Backward difference on left half of gridpoints, and forward difference on right half | ||
|
D. Alternating forward and backward differences, beginning with backward difference at |
Question
6
What is the truncation error term for the 3-point centered difference formula for approximating 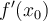 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
7
Let 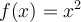 . Approximate
. Approximate 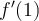 using the 2-point difference formula with
using the 2-point difference formula with 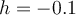 .
.
Choose one answer.
| A. 2.0 | ||
| B. 2.1 | ||
| C. 1.9 | ||
| D. 0.21 | ||
| E. 0.19 |
Question
8
Which of the following statements about composite Newton-Cotes quadrature rules is true?
Choose one answer.
| A. They use a Taylor polynomial for f'. | ||
| B. They integrate a piecewise polynomial approximation to f. | ||
| C. They are a type of Monte Carlo method. | ||
| D. They require orthogonal polynomial integration. | ||
| E. None of the above |
Question
9
Use Simpson's method (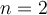 ) to approximate
) to approximate 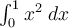 . Choose the best 4 significant digit answer below.
. Choose the best 4 significant digit answer below.
Choose one answer.
| A. 0.3750 | ||
| B. 0.5000 | ||
| C. 0.6667 | ||
| D. 0.3333 | ||
| E. 0.2500 |
Question
10
Use composite trapezoidal rule with 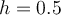 to approximate
to approximate
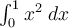 . Choose the best 4 significant digit answer below.
. Choose the best 4 significant digit answer below.
Choose one answer.
| A. 0.3750 | ||
| B. 0.5000 | ||
| C. 0.3333 | ||
| D. 1.500 | ||
| E. 0.3125 |
Question
11
How is the adaptive quadrature method adaptive?
Choose one answer.
| A. Subdivides if the integral is too large. | ||
| B. It subdivides if the derivative is too large. | ||
| C. It subdivides if rounding error exceedes truncation error. | ||
| D. It subdivides if error estimate is too large. |
Question
12
Newton-Cotes quadrature rules for a function f are typically found by doing which of the following?
Choose one answer.
| A. Using a left sided Riemann sum | ||
| B. Approximating f by a polynomial P and integrating P | ||
| C. Integrating a Fourier transform of f and then applying an inverse transform | ||
| D. Finding the average height of f at n randomly generated points | ||
| E. None of the above |
Question
13
In a floating point system with 3 decimal digits in the fractional part, what is the result of 7.234 + 5.784?
Choose one answer.
| A. 13.02 | ||
| B. 13.01 | ||
| C. 13.0 | ||
| D. 13.1 | ||
| E. None of the above |
Question
14
What is the relative error in the 3 decimal digit floating point arithmetic computation (123 + 0.449)-122?
Choose one answer.
| A. 31% | ||
| B. 0.449 | ||
| C. 44.9% | ||
| D. 0 | ||
| E. 1.449 |
Question
15
What value results in the 3 decimal digit floating point arithmetic computation (123.3 + 0.4)-122.7?
Choose one answer.
| A. 1 | ||
| B. 0.4 | ||
| C. 0 | ||
| D. 0 | ||
| E. 1.3 |
Question
16
In a floating point system with t digits in the fractional part, if x and y share the same normalized exponent and the same g fractional digits, then how
many digits of fl(x-y) are known to be correct?
Choose one answer.
| A. t-g | ||
| B. g | ||
| C. All t | ||
| D. 0 | ||
| E. It depends on the compiler. |
Question
17
In general, which of the following holds for the floating point addition of two or three floating point numbers whose sum does not overflow or underflow?
Choose one answer.
| A. Both commutative and associative | ||
| B. Commutative but not associative | ||
| C. Neither commutative nor associative | ||
| D. Associative but not commutative |
Question
18
Swamping and cancellation both describe a loss of information. Select the statement below that best describes their effects.
Choose one answer.
| A. Swamping does not violate the fundamental axiom of floating point arithmetic, but cancellation does. | ||
| B. Cancellation loses precision, while swamping does not. | ||
| C. Swamping loses precision, while cancellation does not. | ||
| D. Swamping can only happen with multiplication and cancellation only with addition. |
Question
19
The machine epsilon is nearest to which of the following?
Choose one answer.
| A. Underflow | ||
| B. Overflow | ||
| C. The distance between 1 and the nearest float to 1 | ||
| D. 1/Overflow |
Question
20
Suppose x and y are floats and fl(x+y)=fl(x). What can be said of y?
Choose one answer.
| A. y underflowed. | ||
| B. y=0. | ||
| C. |y| is less than |x|*(machine epsilon). | ||
| D. fl(0+y)=0. |
Question
21
With a fixed length floating point word, adding a bit to the fractional part requires removing a bit from the exponent. Which of the following statements
describes how this affects the set of floats?
Choose one answer.
| A. The floats are farther apart but have a larger range. | ||
| B. The floats are nearer each other but have a smaller range. | ||
| C. There are more floats. | ||
| D. Underflow is smaller. | ||
| E. The machine precision grows. |
Question
22
Suppose a floating point system can represent K floats. If one bit is added to that floating point word, about how many floats can then be represented?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
23
What can be said of any solution, x, to fl(1+x)=1?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
24
Fill in the blank. If it can be shown that the result of a computation is the exact answer to a nearby problem, then we say the computation is
____________.
Choose one answer.
| A. Highly accurate | ||
| B. Rounding correct | ||
| C. Backward stable | ||
| D. Well conditioned | ||
| E. Robust |
Question
25
If x + y is smaller than both x and y, information in the sum x + y is lost. What is this called?
Choose one answer.
| A. Swamping | ||
| B. Machine epsilon | ||
| C. Truncation error | ||
| D. Cancellation | ||
| E. None of the above |
Question
26
Fill in the blank. If a small change to a problem leads to a large change in its solution, then we say that the problem is ______________.
Choose one answer.
| A. Backward stable | ||
| B. Well conditioned | ||
| C. Robust | ||
| D. Ill conditioned | ||
| E. Highly accurate |
Question
27
Problem 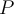 has input
has input 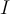 and output
and output 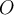 . A small perturbation
. A small perturbation 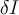 gives a new input
gives a new input 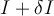 and a new output
and a new output 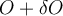 . A relative condition number
. A relative condition number 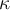 for problem
for problem 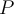 should satisfy which of the following?
should satisfy which of the following?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
28
Problem 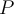 has input
has input 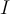 and output
and output 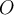 . A small perturbation
. A small perturbation 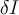 gives a new input
gives a new input 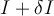 and a new output
and a new output 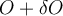 . An absolute condition number
. An absolute condition number 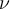 for problem
for problem 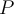 should satisfy which of the following?
should satisfy which of the following?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
29
Under what conditions on a problem and method are we guaranteed a good solution?
Choose one answer.
| A. Problem is stable and method is backward stable. | ||
| B. Problem is stable and method is well conditioned. | ||
| C. Problem is well conditioned and method is well conditioned. | ||
| D. Problem is well conditioned and method is backward stable. |
Question
30
What is an upper bound on the relative error between two neighboring floats called?
Choose one answer.
| A. Cancellation limit | ||
| B. Machine epsilon | ||
| C. Underflow | ||
| D. Backward error | ||
| E. None of the above |
Question
31
In a floating point system with 3 decimal digits in the fractional part, what floating point number would be used to represent 0.0032419?
Choose one answer.
| A. 0.003 | ||
| B. 0.00324 | ||
| C. 0.003242 | ||
| D. 0.00 | ||
| E. None of the above |
Question
32
In a floating point system with 3 decimal digits in the fractional part, what floating point number would be used to represent 142.32419?
Choose one answer.
| A. 142 | ||
| B. 142.324 | ||
| C. 142.3 | ||
| D. 142.32 | ||
| E. None of the above |
Question
33
When a large magnitude and small magnitude float are added, information from the smaller number is lost. What is this called?
Choose one answer.
| A. Chopping | ||
| B. Cancellation | ||
| C. Truncation Error | ||
| D. Swamping | ||
| E. Tail Error |
Question
34
The term Initial Value Problem is best defined in this course as which of the following?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. Given |
||
|
D. Find |
||
|
E. |
Question
35
Which of the following is an initial value problem?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
36
A shooting method for a boundary value problem requires what 2 numerical methods?
Choose one answer.
| A. An interpolator and a numerical differentiation rule | ||
| B. A quadrature rule and an IVP solver | ||
| C. A root finder and a quadrature rule | ||
| D. An IVP solver and a root finder |
Question
37
What is the Euler slope?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of the above |
Question
38
In theory, the error in Euler's method can be made arbitrarily small by varying h, why is this not the case in practice?
Choose one answer.
| A. Because of rounding errors | ||
| B. Because of truncation errors | ||
|
C. As |
||
|
D. As |
Question
39
When converting a scalar differential equation of order n into a system of first order differential equations, how many dimensions are needed to represent
the solution vector?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of the above |
Question
40
Why does an explicit 3-step method for IVP require the use of a single-step method?
Choose one answer.
|
A. Because it averages 3 values in |
||
| B. Because Euler's method is unstable | ||
| C. Because the corrector needs a prediction | ||
| D. Because a 3-step method needs 2 previous approximations to y | ||
| E. Because a 3-step method needs 3 previous approximations to y |
Question
41
An explicit 3 step method needs to use a single step method, but Euler's method is a bad choice. Why shouldn't one use Euler's method in this setting?
Choose one answer.
| A. Euler's method is unstable. | ||
|
B. Eulers method has local truncation error |
||
| C. Euler's method has large rounding errors. | ||
| D. Euler's method is too slow for a 3 step method. | ||
| E. Taylor methods are more general. |
Question
42
In a multistep predictor-corrector method, what type of method is the corrector?
Choose one answer.
| A. The corrector is typically a higher order Runge Kutta method. | ||
| B. The corrector is typically a low order Runge Kutta method. | ||
| C. The corrector is typically an implicit method. | ||
| D. The corrector is typically a higher order explicit multistep method. |
Question
43
The Adams-Bashforth 2-step (AB2) method has the iteration 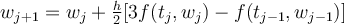 . Consider the IVP
. Consider the IVP 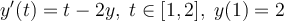 . Select the best 4
significant digit approximation below to the AB2 value for
. Select the best 4
significant digit approximation below to the AB2 value for 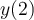 , taking
, taking 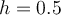 i,
i, 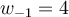 and
and 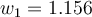 .
.
Choose one answer.
| A. 1.297 | ||
| B. 1.015 | ||
| C. 0.7650 | ||
| D. 1.547 |
Question
44
How many function evaluations are required per timestep for an Adams-Bashforth method of order 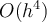 ?
?
Choose one answer.
| A. 1 | ||
| B. 2 | ||
| C. 4 | ||
| D. 5 | ||
| E. 6 |
Question
45
Which of the following is an implicit method?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
46
Which of the following is a general purpose single step method?
Choose one answer.
| A. Taylor's method | ||
| B. Adams-Bashforth's method | ||
| C. Adams-Moulton's method | ||
| D. Runge-Kutta's method |
Question
47
Consider the IVP 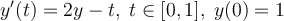 . Approximate
. Approximate 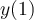 using Euler's method with
using Euler's method with 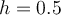 . Select the best 3 significant digit answer below.
. Select the best 3 significant digit answer below.
Choose one answer.
| A. 3.00 | ||
| B. 3.75 | ||
| C. 2.00 | ||
| D. 4.55 | ||
| E. 6.30 |
Question
48
Variable step-size methods all require which of the following?
Choose one answer.
| A. A good starting guess | ||
| B. An error estimate | ||
| C. Multistep method | ||
| D. A list of allowable step sizes |
Question
49
Choose the iteration below which represents the Runge-Kutta method called the midpoint method.
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
50
Choose the iteration below which represents the Runge-Kutta method called the modified Euler or Heun's method.
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
51
How many function evaluations are required per timestep for a Runge-Kutta method of order 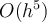 ?
?
Choose one answer.
| A. 1 | ||
| B. 2 | ||
| C. 4 | ||
| D. 5 | ||
| E. 6 |
Question
52
How many function evaluations are required per timestep for a Runge-Kutta method of order 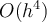 ?
?
Choose one answer.
| A. 1 | ||
| B. 2 | ||
| C. 4 | ||
| D. 5 | ||
| E. 6 |
Question
53
Consider the IVP 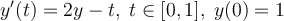 . Which of the following
iterations correspond to the Taylor method of order 2 for this IVP?
. Which of the following
iterations correspond to the Taylor method of order 2 for this IVP?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
54
If an IVP is stiff, what restriction is imposed on the solver?
Choose one answer.
| A. Stiff IVP's require a small timestep. | ||
| B. Stiff IVP's require predictor-corrector methods. | ||
| C. Stiff IVP's require Taylor methods. | ||
| D. Stiff IVP's require high order methods. |
Question
55
What qualitative property should a method have when applied to the test problem 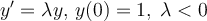 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
56
Why are Taylor methods not as general purpose as Runge-Kutta methods?
Choose one answer.
|
A. Taylor methods require the evaluation of |
||
| B. Taylor polynomials oscilate too much. | ||
| C. Taylor methods replace derivatives with function evaluations. | ||
| D. Taylor methods are not parallelizable because of nested function evaluations. |
Question
57
Fill in the blank. Ignoring rounding errors, a successful IVP method with local truncation error of order k should have global error of order ________.
Choose one answer.
| A. k+1 | ||
| B. k/2 | ||
| C. 2k | ||
| D. k-1 |
Question
58
All single step IVP methods have a common iteration 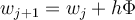 . If
. If 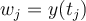 , what is the value of
, what is the value of 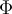 that would guarantee
that would guarantee 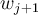 was on the solution curve?
was on the solution curve?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
59
What conditions on an initial value problem guarantee a unique solution?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. The initial |
||
|
E. |
Question
60
Fill in the blank. A second order ordinary differential equation, 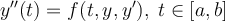 requires two extra conditions for uniqueness of solution. If these conditions are
requires two extra conditions for uniqueness of solution. If these conditions are 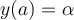 and
and 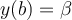 , then the differential equation is called a(n) ___________.
, then the differential equation is called a(n) ___________.
Choose one answer.
| A. Partial differential equation | ||
| B. Ill posed differential equation | ||
| C. Side-condition differential equation | ||
| D. Boundary value problem |
Question
61
Which of the following gives sufficient conditions for 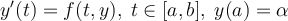 to have a unique solution?
to have a unique solution?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
62
The Weierstrauss approximation theorem says that under certain conditions on 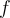 and for any
and for any 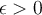 , there is a polynomial
, there is a polynomial 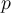 , such that
, such that 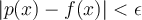 for all
for all 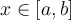 . Choose from below the weakest such conditions on
. Choose from below the weakest such conditions on 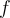 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
63
Which of the following is true for 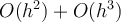 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
64
Which of the following is true for 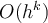 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
65
What is the minimum number of multiplications required to evaluate 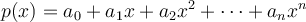 for arbitrary real
for arbitrary real 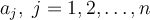 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
66
When dividing a polynomial 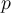 of degree
of degree 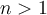 by the polynomial
by the polynomial  , the remainder will be a scalar. What choice below best describes this
scalar?
, the remainder will be a scalar. What choice below best describes this
scalar?
Choose one answer.
|
A. It has degree |
||
|
B. It is |
||
|
C. It is |
||
|
D. It is a root of |
||
| E. It is deflated. |
Question
67
Let 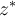 be a zero of a polynomial
be a zero of a polynomial 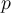 of degree n > 10, and suppose we have an initial approximation
of degree n > 10, and suppose we have an initial approximation
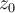 such that both Newton's method and the secant
method both converge, and an interval
such that both Newton's method and the secant
method both converge, and an interval 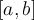 of length
about
of length
about 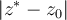 containing
containing 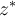 and for which bisection will converge to
and for which bisection will converge to 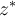 . For this specialized case, list from fastest to slowest, the three
methods.
. For this specialized case, list from fastest to slowest, the three
methods.
Choose one answer.
| A. Newton's, secant, bisection | ||
| B. Newton's, bisection, secant | ||
| C. Secant, Newton's, bisection | ||
| D. Secant, bisection, Newton's | ||
| E. Bisection, Newton's, secant |
Question
68
Fill in the blank. If 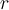 is a root of a polynomial
is a root of a polynomial
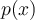 of degree
of degree 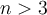 , then
, then 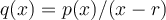 is a polynomial of degree
is a polynomial of degree 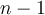 . Finding the remaining roots of
. Finding the remaining roots of 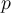 by finding the roots of
by finding the roots of 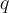 is called ______________.
is called ______________.
Choose one answer.
| A. The Chinese remainder method | ||
| B. Degree slashing | ||
| C. Synthetic division | ||
| D. Deflation |
Question
69
Why don't we use the quintic equation to find the zeros of a polynomial of degree 5 or less?
Choose one answer.
| A. Newton's method is more accurate. | ||
|
B. Extracting |
||
| C. It is pretend. | ||
| D. Rounding errors and truncation errors work against each other. |
Question
70
A Hermite interpolator is constructed for values and slopes at 4 knots. What can be said about the degree of this interpolator?
Choose one answer.
| A. Its degree is 4. | ||
| B. Its degree is no more than 4. | ||
| C. Its degree is no more than 7. | ||
| D. Its degree must be more than 7. | ||
| E. None of the above |
Question
71
What type of polynomial interpolator would be appropriate for the data 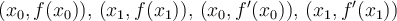 ?
?
Choose one answer.
| A. Hermite | ||
| B. Taylor | ||
| C. Lagrange | ||
| D. Piecewise linear | ||
| E. Quadratic spline |
Question
72
If 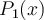 is the Lagrange interpolator for the knots
is the Lagrange interpolator for the knots
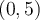 and
and 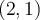 , what is
, what is 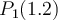 ?
?
Choose one answer.
| A. 2.6 | ||
| B. 2.8 | ||
| C. 3.9 | ||
| D. 1.5 | ||
| E. 2.9 |
Question
73
Suppose we approximate 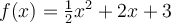 over
over 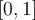 using the Lagrange interpolator
using the Lagrange interpolator 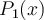 for the nodes
for the nodes 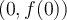 and
and 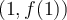 . Use the Lagrange error term (remainder) to get an upper bound on the
error.
. Use the Lagrange error term (remainder) to get an upper bound on the
error.
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. There is no error; it is well posed. |
Question
74
How many polynomials exist which interpolate the data 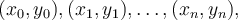 where
where 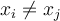 for
for 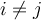 ?
?
Choose one answer.
| A. Only one | ||
| B. Depends upon the knot positions | ||
| C. n+1 Lagrange basis functions | ||
| D. Infinitely many |
Question
75
Suppose 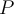 is the Lagrange interpolator for the knots
is the Lagrange interpolator for the knots
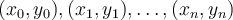 with
with 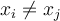 for
for 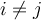 . If
. If 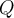 is a polynomial of degree
is a polynomial of degree 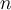 satisfying
satisfying 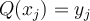 , for
, for 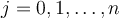 . What can be said of
. What can be said of 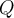 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of the above |
Question
76
If 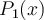 is the Lagrange interpolator for the knots
is the Lagrange interpolator for the knots
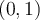 and
and 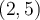 , what is
, what is 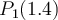 ?
?
Choose one answer.
| A. 4.1 | ||
| B. 3.8 | ||
| C. 3.9 | ||
| D. 3.5 | ||
| E. 2.9 |
Question
77
A Taylor polynomial is a special case of what type of interpolator?
Choose one answer.
| A. Osculating polynomial | ||
| B. Lagrange interpolator | ||
| C. Hermite interpolator | ||
| D. Vandermonde interpolator | ||
| E. None of the above |
Question
78
Consider the Lagrange basis functions for the knots 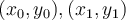 , and
, and 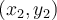 . How many basis functions are there
for this set of knots, and what are their degrees?
. How many basis functions are there
for this set of knots, and what are their degrees?
Choose one answer.
| A. Three basis functions, each of degree 2 | ||
| B. Two basis functions, each of degree two | ||
| C. Two basis functions, each of degree three | ||
| D. Three basis functions, of degree 1, degree 2 and degree 3 |
Question
79
Let 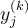 be the value of the
be the value of the 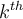 derivative of a curve at the point
derivative of a curve at the point 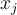 . Suppose we want to interpolate the data
. Suppose we want to interpolate the data 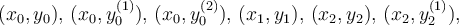 and
and 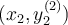 . If a Vandermonde matrix is constructed for the interpolating
polynomial, what is its size?
. If a Vandermonde matrix is constructed for the interpolating
polynomial, what is its size?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
80
Let 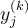 be the value of the
be the value of the 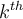 derivative of a curve at the point
derivative of a curve at the point 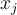 . Suppose we want to interpolate the data
. Suppose we want to interpolate the data 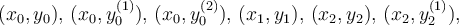 and
and 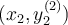 . In general, what is the degree of such an interpolating
polynomial?
. In general, what is the degree of such an interpolating
polynomial?
Choose one answer.
| A. 4 | ||
| B. 5 | ||
| C. 6 | ||
| D. 7 |
Question
81
If 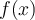 is smooth enough in a neighborhood of
is smooth enough in a neighborhood of
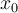 , then the Taylor polynomial of degree n for
, then the Taylor polynomial of degree n for
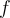 at
at 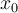 approximates
approximates 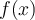 with error_________.
with error_________.
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of the above |
Question
82
What is the Taylor polynomial of degree 1 for 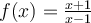 at
at
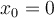 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
83
What is the Taylor polynomial of degree 1 for 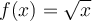 at
at
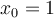 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
84
The linear Taylor polynomial at 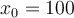 for
for 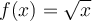 is
is 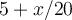 . Use this Taylor polynomial to approximate
. Use this Taylor polynomial to approximate 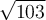 . Select the best 5 significant digit answer to the Taylor approximation.
. Select the best 5 significant digit answer to the Taylor approximation.
Choose one answer.
| A. 10.149 | ||
| B. 10.150 | ||
| C. 5.5074 | ||
| D. 9.8500 | ||
| E. 10.001 |
Question
85
The set of polynomials of degree n over a field is a vector space of which dimension?
Choose one answer.
| A. n | ||
| B. 2n | ||
| C. n+2 | ||
| D. n/2 | ||
| E. None of the above |
Question
86
The method of bisection can find a zero of a continuous function, if which of the following is true of the initial data?
Choose one answer.
| A. It is close to the correct answer. | ||
| B. It gives the bisector of the zero. | ||
| C. It is not complex. | ||
| D. It gives function height and slope. | ||
| E. None of the above |
Question
87
Bisection is used on an initial interval [a,b], where b-a=2. How many iterations are required for the current interval to have length 1/16?
Choose one answer.
| A. 4 | ||
| B. 5 | ||
| C. 6 | ||
| D. 8 | ||
| E. 10 |
Question
88
If the method of bisection is used to find a zero of a continuous function f(x), and an initial interval [a,b] is given such that f(a)f(b) < 0, counting
multiplicity, what can be said about the zeros of f in [a,b]?
Choose one answer.
| A. f has exactly one zero in [a,b]. | ||
| B. f has 0, 1, or infinitely many zeros in [a,b]. | ||
| C. f has an even number of zeros in [a,b]. | ||
| D. f has an odd number of zeros in [a,b]. |
Question
89
Which method cannot be used to find a root of 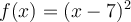 ?
?
Choose one answer.
| A. Newton's method | ||
| B. Bisection method | ||
| C. Secant method | ||
| D. Meuller's method | ||
| E. False position |
Question
90
Suppose it is known that the continuous function 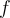 has exactly 1 root strictly between 0 and 1, and it is not a double root. Which method can guarantee an approximate root with error less than 0.0001 in
fewer than 14 function evaluations?
has exactly 1 root strictly between 0 and 1, and it is not a double root. Which method can guarantee an approximate root with error less than 0.0001 in
fewer than 14 function evaluations?
Choose one answer.
| A. Newton's method | ||
| B. Secant method | ||
| C. Bisection method | ||
| D. None of the above |
Question
91
Suppose it is known that the continuous function 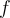 has exactly 1 root strictly between 0 and 1, and it is a double root. An encrypted subroutine will return
has exactly 1 root strictly between 0 and 1, and it is a double root. An encrypted subroutine will return 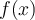 given any
given any 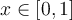 . Which of the following methods cannot be applied to this problem?
. Which of the following methods cannot be applied to this problem?
Choose one answer.
| A. Neither Newton's nor bisection can be applied here. | ||
| B. Neither Newton's nor secant can be applied here. | ||
| C. Bisection cannot be applied here. | ||
| D. Newton's method cannot be applied here. |
Question
92
Which of the following gives a rough estimate of convergence for bisection and Newton's method (in the case each converge at their respective order of
convergence)?
Choose one answer.
| A. For each iteration, Newton's method adds 1 correct bit and bisection add about 0.5 correct bits. | ||
| B. For each of the two iterations, Newton's method doubles number of correct bits and bisection adds 2 correct bits. | ||
| C. For each iteration, Newton's method doubles the number of correct bits and bisection adds 1 correct bit. | ||
| D. For each iteration, Newton's method adds two correct bits and bisection adds 1 correct bit. |
Question
93
Suppose Newton's method begins with an initial approximation, x0. The next approximation, x1, is found by doing which of
the following?
Choose one answer.
|
A. Linearizing |
||
|
B. Bisecting the line from |
||
|
C. Approximating |
||
|
D. Approximating |
||
| E. None of the above |
Question
94
Let 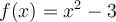 and
and 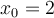 . Use Newton's method to find
. Use Newton's method to find 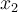 .
.
Identify the approximation below that is correct to 6 significant digits.
Identify the approximation below that is correct to 6 significant digits.
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
95
What do we mean when we say Newton's method is not a general purpose method?
Choose one answer.
| A. It does not always converge. | ||
| B. It may divide by zero. | ||
| C. It requires the evaluation of f'. | ||
| D. It may get stuck in a cycle. | ||
| E. It requires complex arithmetic. |
Question
96
Which of the following is a Newton iteration to find 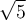 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
97
Which of the following is a Newton iteration to find 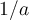 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
Question
98
The secant method begins with two approximations, 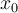 and
and 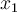 , to a zero of
, to a zero of 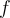 . The next point,
. The next point, 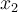 is found by doing which of the following?
is found by doing which of the following?
Choose one answer.
|
A. Using the secant angle between |
||
| B. Averaging the Newton method and the bisection method | ||
|
C. Approximating |
||
|
D. Finding the x-intercept of the line joining |
||
| E. None of the above |
Question
99
The secant method requires how many function evaluations to complete k iterations?
Choose one answer.
| A. k-1 | ||
| B. k | ||
| C. k+1 | ||
| D. k+2 | ||
| E. 2k |
Question
100
Let 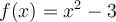 ,
, 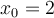 and
and 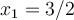 . Use the secant method to find
. Use the secant method to find 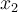 . Identify the approximation below that is correct to 6 significant
digits.
. Identify the approximation below that is correct to 6 significant
digits.
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |