1
Which of the following statements about ordinary differential equations is true?
Choose one answer.
| a. They may contain one independent variable. | ||
| b. They are composed of one or more derivatives with respect to the independent variable. | ||
| c. They do not contain partial derivatives. | ||
| d. All of the above |
Question
2
Find the solution for the following differential equation for 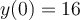 .
.
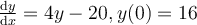
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
3
Find the solution for the following differential equation for 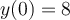 .
.
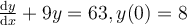
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
4
Find the solution for the following differential equation for 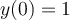 .
.
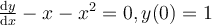
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
5
Find the solution for the following differential equation for 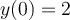 .
.
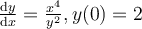
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
6
Find the solution for the following differential equation for 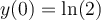 .
.
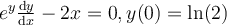
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
7
Find the solution for the following differential equation for 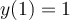 .
.
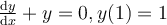
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
8
Find the solution for the following differential equation for 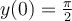 .
.
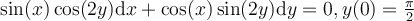
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
9
Find the solution for the following differential equation for 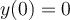 .
.
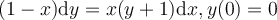
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
10
Find the solution for the following differential equation for 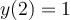 .
.
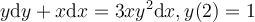
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
11
Find the solution for the following differential equation for 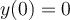 .
.
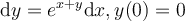
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
12
Which of the following relationships is an ordinary differential equation?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
13
Find the solution for the following differential equation for 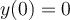 .
.
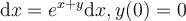
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
14
Determine the order of the following differential equation.
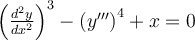
Choose one answer.
| a. 1 | ||
| b. 2 | ||
| c. 3 | ||
| d. 4 |
Question
15
Which of the following classifications pertain to ordinary differential equations?
Choose one answer.
| a. Linear | ||
| b. Nonlinear | ||
| c. Homogeneous | ||
| d. All of the above |
Question
16
Consider the differential equation 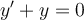 . Suppose that a
student determined the solution to be
. Suppose that a
student determined the solution to be 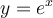 . Based upon
this information, is the student correct?
. Based upon
this information, is the student correct?
Choose one answer.
|
a. No, the student should have determined the solution to be |
||
|
b. No, the student should have determined the solution to be |
||
| c. No, the student should have determined that there is no solution. | ||
| d. Yes, the student did not make any errors. |
Question
17
Apply the superposition principle to find the solution for 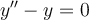 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
18
Find a particular solution for the following differential equation for which 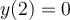 ,
,
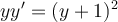 ,
, 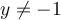 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There is no solution. |
Question
19
Find a particular solution for 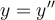 which passes through
the origin and through the point
which passes through
the origin and through the point 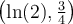 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
20
Find the solution for the following differential equation for 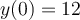 .
.
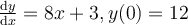
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
21
Find a 1-parameter family of solutions for the following differential equation.
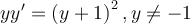
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There is no solution. |
Question
22
Find a particular solution for 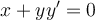 where
where 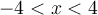 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There is no solution. |
Question
23
The rate at which a radioactive substance decays is proportional to the remaining number of atoms. The differential equation which can be used to describe
this process follows:
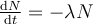
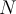 represents the number of atoms remaining after
represents the number of atoms remaining after
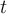 seconds. The proportionality constant
seconds. The proportionality constant 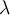 is considered the decay constant for this process. If
is considered the decay constant for this process. If
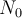 represents the number of remaining atoms at
represents the number of remaining atoms at
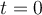 seconds, find the general solution.
seconds, find the general solution.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
24
For a circuit containing a capacitor and resistor, the first-order differential equation that describes a discharging capacitor follows:
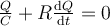
If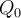 represents the charge within the capacitor at
represents the charge within the capacitor at
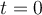 seconds, find the general solution.
seconds, find the general solution. 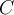 is the capacitance of the capacitor.
is the capacitance of the capacitor. 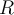 is the resistance of the resistor.
is the resistance of the resistor.
If
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
25
Earth's atmospheric pressure 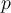 can be modeled by the
following first-order differential equation.
can be modeled by the
following first-order differential equation.
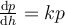
This differential equation describes the rate at which atmospheric pressure changes with altitude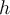 above sea level.
above sea level. 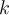 is a constant. If
is a constant. If 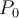 represents the atmospheric pressure (millibars) at sea level
(
represents the atmospheric pressure (millibars) at sea level
(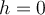 kilometers), find the general solution.
kilometers), find the general solution.
This differential equation describes the rate at which atmospheric pressure changes with altitude
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
26
Consider 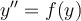 where
where 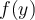 is defined on the interval
is defined on the interval 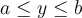 . It is possible to rewrite this second-order differential equation as a
system of two first-order differential equations using an appropriate change of variable. Using
. It is possible to rewrite this second-order differential equation as a
system of two first-order differential equations using an appropriate change of variable. Using 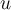 as the new variable, how can
as the new variable, how can 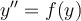 be rewritten as a system of two first-order differential equations?
be rewritten as a system of two first-order differential equations?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
27
Using Picard's Method of Successive Approximations, attempt to find the first four Picard approximations to the solution for 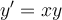 to determine whether or not a solution exists for this first-order
differential equation. It is given that
to determine whether or not a solution exists for this first-order
differential equation. It is given that 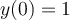 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
28
Construct the direction field for 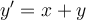 using integer
coordinates from -5 to 5. Analyze the general shape and trajectories. Which of the following represents the equation for a possible integral curve?
using integer
coordinates from -5 to 5. Analyze the general shape and trajectories. Which of the following represents the equation for a possible integral curve?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. None of the above |
Question
29
Which of the following statements about linear ordinary differential equations is true?
Choose one answer.
|
a. Linear ordinary differential equations are of the form |
||
|
b. Linear ordinary differential equations are of the form |
||
| c. Linear ordinary differential equations do not contain partial derivatives. | ||
| d. All of the above |
Question
30
Which of the following is a linear ordinary differential equation?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. None of the above |
Question
31
Find the general solution for the following exact differential equation.
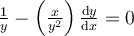
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
32
Find the particular solution for the following separable differential equation.
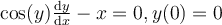
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
33
Find the general solution for the following Bernoulli differential equation.
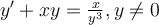
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
34
Find the particular solution for the following homogeneous differential equation.
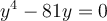 where
where 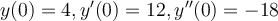 and
and 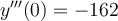
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
35
Find the implicit solution to the following differential equation.
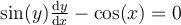
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
36
Solve the following differential equation by separating it:
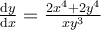
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
37
Solve the following differential equation by separating it:
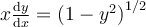
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
38
Find the solution for the following differential equation for 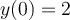 .
.
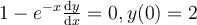
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
39
Find the solution for the following second-order ordinary differential equation.
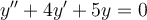 where
where 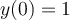 and
and 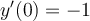
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
40
Consider a mass m that oscillates at the end of a spring having a spring constant 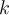 . The following second-order differential equation describes the vertical
displacement y of this spring-mass system.
. The following second-order differential equation describes the vertical
displacement y of this spring-mass system.
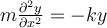
This differential equation neglects the influence of air resistance or frictional forces. Find the general solution which describes the vertical displacement of this spring as a function of time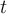 .
.
This differential equation neglects the influence of air resistance or frictional forces. Find the general solution which describes the vertical displacement of this spring as a function of time
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
41
Consider a mass m that oscillates at the end of a spring having a spring constant k. The following second-order differential equation describes the
vertical displacement y of this spring-mass system.
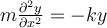
Such a differential equation implies that mass m, once started, will simply oscillate up and down forever! This differential equation neglects the influence of frictional forces. Let us assume that there is a retarding force which is proportional to the velocity of motion where s is treated as a proportionality constant (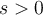 ). The aforementioned
differential equation now becomes the following.
). The aforementioned
differential equation now becomes the following.
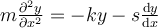
Let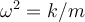 and
and 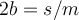 where
where 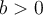 .
.
There are three possible types of solutions which depend upon the relative size of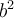 and
and 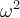 , including the following:
, including the following:
Overdamped if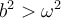 ,
,
Critically damped if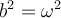 ,
,
Underdamped or oscillatory if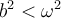 .
.
Find the general solution for this differential equation, which describes the vertical displacement of this spring as a function of time t for "overdamped" motion.
Such a differential equation implies that mass m, once started, will simply oscillate up and down forever! This differential equation neglects the influence of frictional forces. Let us assume that there is a retarding force which is proportional to the velocity of motion where s is treated as a proportionality constant (
Let
There are three possible types of solutions which depend upon the relative size of
Overdamped if
Critically damped if
Underdamped or oscillatory if
Find the general solution for this differential equation, which describes the vertical displacement of this spring as a function of time t for "overdamped" motion.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
42
Consider a mass m that oscillates at the end of a spring having a spring constant k. The following second-order differential equation describes the
vertical displacement y of this spring-mass system.
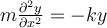
Such a differential equation implies that mass m, once started, will simply oscillate up and down forever! This differential equation neglects the influence of frictional forces. Let us assume that there is a retarding force which is proportional to the velocity of motion where s is treated as a proportionality constant (s > 0). The aforementioned differential equation now becomes the following.
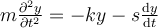
Let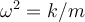 and
and 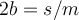 where
where 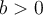 .
.
There are three possible types of solutions which depend upon the relative size of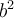 and
and 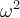 , including the following:
, including the following:
Overdamped if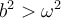 ,
,
Critically damped if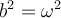 ,
,
Underdamped or oscillatory if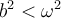 .
.
Find the general solution for this differential equation, which describes the vertical displacement of this spring as a function of time t for the "critically damped" motion.
Such a differential equation implies that mass m, once started, will simply oscillate up and down forever! This differential equation neglects the influence of frictional forces. Let us assume that there is a retarding force which is proportional to the velocity of motion where s is treated as a proportionality constant (s > 0). The aforementioned differential equation now becomes the following.
Let
There are three possible types of solutions which depend upon the relative size of
Overdamped if
Critically damped if
Underdamped or oscillatory if
Find the general solution for this differential equation, which describes the vertical displacement of this spring as a function of time t for the "critically damped" motion.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
43
The one-dimensional time-independent Schrodinger equation is given by the following.
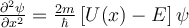
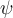 is a wave function which describes the displacement
is a wave function which describes the displacement
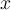 of a single particle of mass
of a single particle of mass 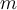 where
where 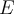 is the total energy,
is the total energy, 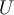 is the potential energy, and
is the potential energy, and 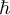 is a well-known constant. Since
is a well-known constant. Since 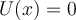 for the particle-in-a-box model where
for the particle-in-a-box model where 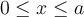 , this second-order differential equation becomes the following.
, this second-order differential equation becomes the following.
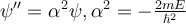
Find the general solution for this differential equation.
Find the general solution for this differential equation.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
44
Find the general solution for this higher-order differential equation.
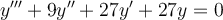
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
45
Find the general solution for this homogeneous ordinary differential equation with constant coefficients (zero right hand side).
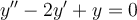
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
46
Find the general solution for this ordinary differential equation with constant coefficients (nonzero right hand side).
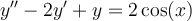
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
47
Find the general solution for this homogeneous ordinary differential equation with variable coefficients. This is an example of an Euler-Cauchy
differential equation (zero right hand side).
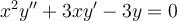
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
48
Find the general solution for this ordinary differential equation with variable coefficients. This is an example of an Euler-Cauchy differential equation
(nonzero right hand side).
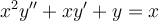
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
49
Find the particular solution for the following non-homogeneous ordinary differential equation.
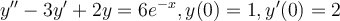
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
50
Apply the linear differential operator 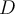 to evaluate
the following expression.
to evaluate
the following expression.
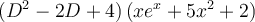
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
51
Find the general solution for the following differential equation using the method of undetermined coefficients.
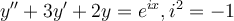
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
52
Which of the following expressions is of the correct form to serve as a trial solution 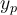 for the following differential equation?
for the following differential equation?
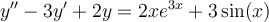
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
53
Find the general solution for the following differential equation using the method of variation of parameters.
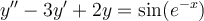
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
54
Which of the following statements regarding the method of undetermined coefficients and variation of parameters is true?
Choose one answer.
| a. The method of variation of parameters is a much more general method than the method of undetermined coefficients which can be used in many cases. | ||
| b. Although the complementary solution is absolutely required when using the method of variation of parameters, it is not required when using the method of undetermined coefficients. | ||
| c. When using the method of variation of parameters, it is possible that the acquired integrals cannot be determined. | ||
| d. All of the above |
Question
55
Find the general solution for the following ordinary differential equation using a method called the reduction of order.
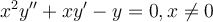
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
56
Given that 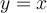 is a solution of
is a solution of 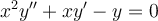 where
where 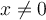 , it is possible to use a method called reduction of order to find the
general solution of the following ordinary differential equation.
, it is possible to use a method called reduction of order to find the
general solution of the following ordinary differential equation.
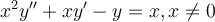
Which of the following expressions would represent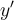 within such a determination?
within such a determination?
Which of the following expressions would represent
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
57
Find the particular solution 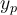 and complementary
function
and complementary
function 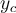 for the following ordinary differential
equation using the method of inverse operators.
for the following ordinary differential
equation using the method of inverse operators.
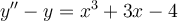
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
58
Suppose that you were asked to find the particular solution 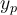 and complementary function
and complementary function 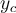 , using the
method of inverse operators, for the following ordinary differential equation.
, using the
method of inverse operators, for the following ordinary differential equation.
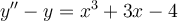
Identify the inverse operator , which might arise
within your solution to this type of problem.
, which might arise
within your solution to this type of problem.
Identify the inverse operator
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
59
Find the power series general solution for the following ordinary differential equation.
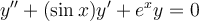
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
60
Which of the following statements are true with regard to a power series solution to the ordinary differential equation 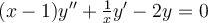 ?
?
Choose one answer.
| a. x = 0 and 1 are ordinary points. | ||
| b. x = 0 and 1 are regular singularities. | ||
| c. x = 0 and 1 are irregular singularities. | ||
| d. Insufficient information has been provided to distinguish whether x = 0 and 1 are ordinary points, regular singularities, or irregular singularities. |
Question
61
Find the series solution for an ordinary differential equation using the Frobenius method.
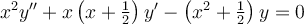
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
62
Which of the following statements most accurately describes how the general solution depends upon the order 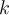 of the Bessel equation shown below?
of the Bessel equation shown below?
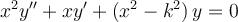
Choose one answer.
|
a. In order to satisfy the Bessel equation, the general solution must be |
||
|
b. In order to satisfy the Bessel equation, the general solution must be |
||
|
c. In order to satisfy the Bessel equation, the general solution must be |
||
|
d. In order to satisfy the Bessel equation, the general solution must be |
||
| e. A and B |
Question
63
Which of the following statements most accurately describes how the general solution for the Bessel equation shown below can depend upon a variety of
well-known functions?
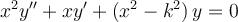
Choose one answer.
|
a. When |
||
|
b. When |
||
|
c. When |
||
| d. All of the above |
Question
64
Find the solution for the following differential equation for 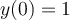 and
and 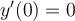 .
.
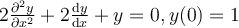 and
and 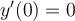
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
65
Find the solution for the following differential equation for 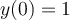 and
and 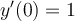 .
.
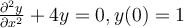 and
and 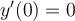
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
66
Find the solution for the following differential equation for which 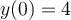 and
and 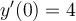 .
.
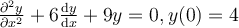 and
and 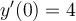
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
67
Find the particular solution for the following non-homogeneous ordinary differential equation.
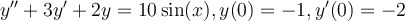
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
68
Find the particular solution for the following non-homogeneous ordinary differential equation.
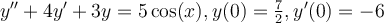
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
69
Find the solution for the following higher-order differential equation.
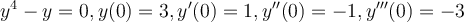
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
70
Find the solution for the following higher-order differential equation.
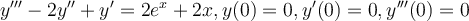
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
71
Find the general solution for the following ordinary differential equation using the variation of parameters method.
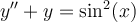
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
72
Find the general solution for the following ordinary differential equation using the method of variation of parameters.
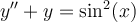
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
73
Find the general solution for the following differential equation using the method of variation of parameters.
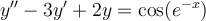
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
74
Find the general solution for the following non-homogeneous ordinary differential equation.
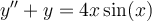
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
75
Find the general solution for the following non-homogeneous ordinary differential equation.
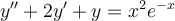
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
76
Find the general solution for the following system of ordinary differential equations.
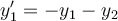
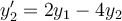
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
77
Suppose that you were given two tanks filled with brine that were connected by pipes. At a rate 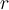 of 10 gallons per minute, the brine is flowing through the first pipe
from the first tank to the second tank. At the same rate
of 10 gallons per minute, the brine is flowing through the first pipe
from the first tank to the second tank. At the same rate 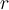 , the brine is flowing through the second pipe from the second tank to the first tank. The initial volume of brine in the first tank is 50 gallons,
and the amount of salt is 15 pounds. The second tank initially contains 25 gallons of pure water. If
, the brine is flowing through the second pipe from the second tank to the first tank. The initial volume of brine in the first tank is 50 gallons,
and the amount of salt is 15 pounds. The second tank initially contains 25 gallons of pure water. If 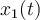 represents the amount of salt in the first tank and
represents the amount of salt in the first tank and 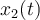 represents the amount of salt in the second tank as a function of
time
represents the amount of salt in the second tank as a function of
time 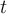 , which of the following statements is true
regarding the system of ordinary differential equations which model this system?
, which of the following statements is true
regarding the system of ordinary differential equations which model this system?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. All of the above |
Question
78
Suppose that you were tasked with creating a system of ordinary differential equations to model predator-prey dynamics. Let x and y denote the number of
prey (e.g., rabbits) and predators (e.g., foxes), respectively, as a function of time 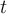 , where
, where 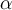 ,
, 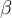 ,
, 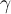 , and
, and 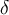 represent parameters that describe how some predator and prey interact
with each other. Which of the following systems of first-order nonlinear ordinary differential equations describe such a system?
represent parameters that describe how some predator and prey interact
with each other. Which of the following systems of first-order nonlinear ordinary differential equations describe such a system?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
79
Consider a mass m that oscillates at the end of a spring having a spring constant 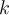 . The following second-order differential equation describes the vertical
displacement
. The following second-order differential equation describes the vertical
displacement 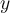 of this spring-mass system.
of this spring-mass system.
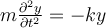
Such a differential equation implies that mass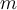 ,
once started, will simply oscillate up and down forever! This differential equation neglects the influence of frictional forces. Let us assume that there
is a retarding force which is proportional to the velocity of motion where
,
once started, will simply oscillate up and down forever! This differential equation neglects the influence of frictional forces. Let us assume that there
is a retarding force which is proportional to the velocity of motion where 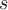 is treated as a proportionality constant (
is treated as a proportionality constant (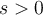 ). The aforementioned differential equation now becomes the
following.
). The aforementioned differential equation now becomes the
following.
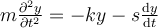
Let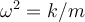 and
and 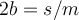 where
where 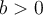 .
.
There are three possible types of solutions which depend upon the relative size of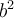 and
and 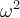 , including the following:
, including the following:
Overdamped if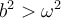 ,
,
Critically damped if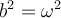 ,
,
Underdamped or oscillatory if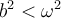 .
.
Which of the following differential equations can be used to describe one of these cases?
Such a differential equation implies that mass
Let
There are three possible types of solutions which depend upon the relative size of
Overdamped if
Critically damped if
Underdamped or oscillatory if
Which of the following differential equations can be used to describe one of these cases?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. Each general solution corresponds to one of the given cases. |
Question
80
Which of the following statements is true regarding the Lotka-Volterra Predator-Prey Model shown below?
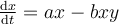
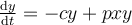
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. All of the above |
Question
81
Which of the following statements is true regarding the differential equations used to describe the double pendulum shown below?
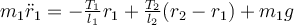
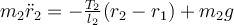
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
||
| e. All of the above |
Question
82
Using existence and uniqueness theorems, identify which of the following statements is true regarding the ordinary differential equation 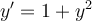 , where
, where 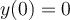 .
.
Choose one answer.
| a. There exists a solution. | ||
| b. The solution exists in some open interval centered at 0. | ||
| c. The solution exists and is unique in some (possibly smaller) interval centered at 0. | ||
| d. All of the above |
Question
83
It is possible to convert an nth order differential equation into an n-dimensional system of first-order differential equations. For the following
4th-order differential equation, identify the corresponding 4-dimensional system of first-order ordinary differential equations.
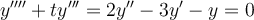
Use the following four new variables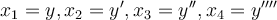 to make this
determination.
to make this
determination.
Use the following four new variables
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
84
There are a variety of methods borrowed from linear algebra that are very useful for finding the solution for systems of linear ordinary differential
equations. One such method includes the usage of matrices. For the following system of linear ordinary differential equations, use these methods to arrive
at the solution in matrix form.
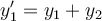
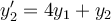
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
85
Find the general solution for the following system of ordinary differential equations.
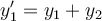
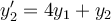
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
86
Find the general solution for the following system of ordinary differential equations.
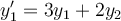
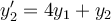
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
87
Which of the following statements describe how integral transforms can be used to reduce the complexity of selected classes of mathematics problems?
Choose one answer.
| a. An integral transform is an operator (e.g., map one function to another function). | ||
| b. The use of selected integral transforms can be used to turn differential equations subject to particular boundary conditions into much simpler algebra problems. | ||
| c. The solution that arises as a result of the use of selected integral transforms must be inverted to represent the solution of the original differential equation. | ||
| d. All of the above |
Question
88
Using Laplace transforms, find the solution for the following ordinary differential equation.
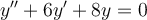 , where
, where 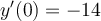 and
and 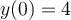
Make sure to also identify the specific Laplace transform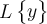 that was used to arrive at your final solution.
that was used to arrive at your final solution.
Make sure to also identify the specific Laplace transform
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
89
Which of the following statements best describes spectra associated with selected Laplace transforms?
Choose one answer.
| a. It is possible to use a Laplace transform power spectrum as a basic tool for the complex-exponential decomposition of finite-duration continuous functions. | ||
| b. It is possible to use a Laplace transform power spectrum within selected applications which include pole-zero estimation. | ||
| c. It is not possible to use a Laplace transform power spectrum as a basic tool for the complex-exponential decomposition of finite-duration continuous functions. | ||
| d. A and B are both correct. |
Question
90
Find the inverse Laplace transform for 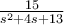 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
91
Find the solution for the following initial value problem using Laplace transforms.
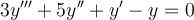 , where
, where 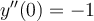 ,
, 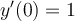 and
and 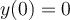
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
92
Using Laplace transforms, find the solution for the following ordinary differential equation.
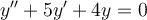 , where
, where 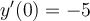 and
and 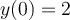
Make sure to also identify the specific Laplace transform that was used to arrive at your final solution.
that was used to arrive at your final solution.
Make sure to also identify the specific Laplace transform
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
93
Using Laplace transforms, find the solution for the following ordinary differential equation.
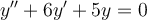 , where
, where 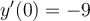 and
and 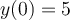
Make sure to also identify the specific Laplace transform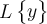 that was used to arrive at your final solution.
that was used to arrive at your final solution.
Make sure to also identify the specific Laplace transform
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
94
The Verlet Method can be used to approximate the solutions for Newton's Laws of Motion. If r denotes the position of a particle as a function of time with
acceleration a where t represents some small time increment, determine which of the following expressions represents an approximate solution for the
position of this particle.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
95
Predictor-Corrector Methods can be used to approximate the solution for a variety of ordinary differential equations. For the following differential
equation, determine which of the following expressions represents an approximate solution. Let h denote the step size where the trapezoidal rule is
employed.
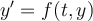 where
where 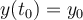
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
96
The Runge-Kutta Method can be used to approximate the solution for a variety of ordinary differential equations. For the following differential equation,
determine which of the following expressions represents an approximate solution using the Runge-Kutta 4th Order Method.
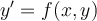 where
where 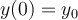
Let h denote the step size where …
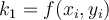
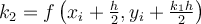
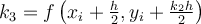
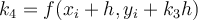
Let h denote the step size where …
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
97
The Adam-Bashforth and Adams-Moulton Methods can be used to approximate the solution for a variety of ordinary differential equations. For the following
differential equation, determine an approximate solution for 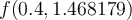 using the 4 Point Adams-Bashforth Method.
using the 4 Point Adams-Bashforth Method.
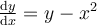 where
where 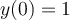 and the step size is 0.1.
and the step size is 0.1.
Choose one answer.
| a. -1.308179 | ||
| b. 0.308179 | ||
| c. 1.308179 | ||
| d. 2.308179 |
Question
98
Find an exact solution for the Lotka-Voltera equations shown below.
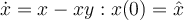
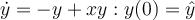
Which of the following represent this solution in parametric form?
Which of the following represent this solution in parametric form?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
99
Which of the following statements correctly describes how nonlinear ordinary differential equations can be used to model selected inverted pendulum
dynamics?
Choose one answer.
| a. They can be used to model inverted pendulum dynamics involving a stationary pivot point. | ||
| b. They can be used to model inverted pendulum dynamics where the inverted pendulum is on a cart consisting of a horizontally moving base. | ||
| c. They can be used to model inverted pendulum dynamics where the inverted pendulum is connected to a massless oscillating base. | ||
| d. All of the above |
Question
100
Which of the following statements correctly describes how nonlinear ordinary differential equations can be used to model selected double pendulum dynamics?
Choose one answer.
| a. They can be used to model double pendulums composed of two simple pendulums. | ||
| b. They can be used to model double pendulums composed of two compound pendulums. | ||
| c. They can be used to model double pendulums composed of two limbs of equal or unequal lengths and/or masses | ||
| d. All of the above |
Question
101
Find the general solution for the Riccati equation shown below.
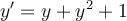
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
102
Which of the following statements describe how Nurgaliev's law can be used to model population dynamics?
Choose one answer.
| a. The solution for this differential equation can be used to make predictions regarding the size of the population as a function of time which is measured in years. | ||
| b. The solution for this differential equation takes into consideration the probability associated with the birth of males or females within a given year. | ||
| c. The solution for this differential equation takes into consideration the probability associated with the death of a person within a given year. | ||
| d. All of the above |