1
Which of the following is NOT a correct description of the sphere of radius 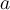 in
in 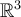 centered at the origin?
centered at the origin?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 2
Which of the following functions DOES NOT have periodic boundary conditions on
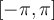 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 3
Which of the following functions DOES NOT have periodic boundary conditions on  ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 4
What minimal combination of the following three conditions ensures the solution of the Laplace equation 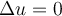 on a bounded domain
on a bounded domain 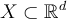 with piecewise smooth boundary must be identically 0 throughout the entire domain
with piecewise smooth boundary must be identically 0 throughout the entire domain 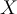 ?
?
I.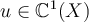
II.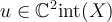
III.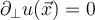 , for all
, for all 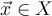
I.
II.
III.
Choose one answer.
|
a. I, II, and III |
||
|
b. II only |
||
|
c. Both I and III |
||
|
d. Both II and III |
Question 5
Assume 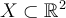 is a domain with piecewise smooth boundary,
is a domain with piecewise smooth boundary, 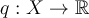 , and
, and 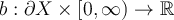 are continuous functions. Which of the following must be true of any function satisfying the nonhomogeneous Laplace equation
are continuous functions. Which of the following must be true of any function satisfying the nonhomogeneous Laplace equation 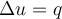 ?
?
I. Either
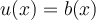 for every
for every 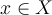 ,
,
or
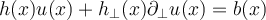 , for every
, for every 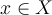 ,
,
where are nonnegative functions and h is nontrivial.
II.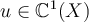
III.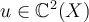
I. Either
or
where are nonnegative functions and h is nontrivial.
II.
III.
Choose one answer.
|
a. Both I and II |
||
|
b. III only |
||
|
c. I, II, and III |
||
|
d. I only |
Question 6
Let 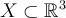 be a domain with piecewise smooth boundary and suppose that the continuously differentiable function
be a domain with piecewise smooth boundary and suppose that the continuously differentiable function 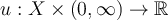 satisfies the heat equation
satisfies the heat equation 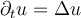 and is nontrivial on
and is nontrivial on 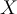 . Which of the following conditions might be true?
. Which of the following conditions might be true?
I.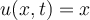 , for all
, for all 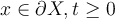 .
.
II.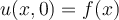 , where
, where  is not identically zero on
is not identically zero on 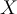 .
.
III.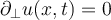 , for all
, for all 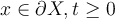 .
.
I.
II.
III.
Choose one answer.
|
a. I or II |
||
|
b. I or III |
||
|
c. II or III |
||
|
d. I, II, or III |
Question 7
Which of the following is an orthonormal set of vectors in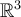 ?
?
Choose one answer.
a. 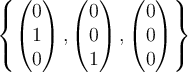 |
||
b. 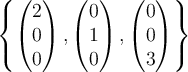 |
||
c. 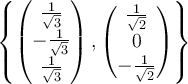 |
||
d. 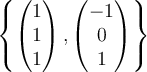 |
Question 8
Let 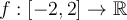 be a continuous function. Which of the following is the
be a continuous function. Which of the following is the 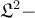 norm of
norm of  ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 9
Which of the following function is NOT in 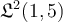 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 10
Which of the following statements, if any, are false?
I.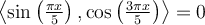 , where the inner product is for the space
, where the inner product is for the space 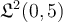 .
.
II.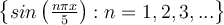 is an orthonormal set of functions in
is an orthonormal set of functions in 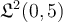 .
.
III.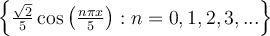 is an orthogonal set of functions in
is an orthogonal set of functions in 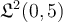 .
.
I.
II.
III.
Choose one answer.
|
a. Both I and III |
||
|
b. Both II and III |
||
|
c. III only |
||
|
d. II only |
Question 11
Which of the following statements guarantees that 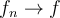 in
in 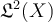 , where
, where 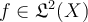 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 12
Fill in the blank. If 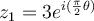 and
and 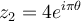 , then
, then 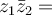 _____.
_____.
Choose one answer.
|
a. -12 |
||
|
b. |
||
|
c. |
||
|
d. |
Question 13
Suppose 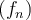 is a sequence of real-valued functions in
is a sequence of real-valued functions in 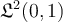 and that
and that 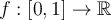 is a given function. Which of the following statements must be true?
is a given function. Which of the following statements must be true?
I.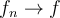 uniformly on
uniformly on 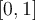 .
.
II. is a continuous function.
is a continuous function.
III.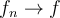 in
in 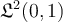 .
.
I.
II.
III.
Choose one answer.
|
a. Both I and II |
||
|
b. Both I and III |
||
|
c. Both II and III |
||
|
d. I, II, and III |
Question 14
Which of these statements, if any, is true?
I.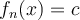 , where
, where 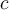 is a positive constant, belongs to
is a positive constant, belongs to 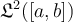 , for any choice of
, for any choice of 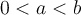 .
.
II. If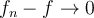 in
in 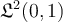 , then
, then  is continuous on
is continuous on 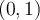 .
.
I.
II. If
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Both I and II |
||
|
d. Neither I nor II |
Question 15
Define 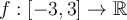 by
by
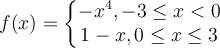
Which of the following is equal to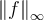 ?
?
Which of the following is equal to
Choose one answer.
|
a. 81 |
||
|
b. -2 |
||
|
c. 0 |
||
|
d. 1 |
Question 16
Which of the following statements is true?
I. If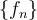 is uniformly convergent on
is uniformly convergent on 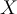 , then
, then 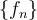 is convergent in the sense of
is convergent in the sense of 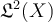 .
.
II. If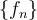 is convergent in the sense of
is convergent in the sense of 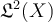 , then
, then 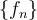 is pointwise convergent on
is pointwise convergent on 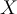 .
.
III. If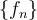 is pointwise convergent on
is pointwise convergent on 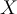 , then
, then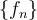 is convergent in the sense of
is convergent in the sense of 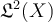 .
.
I. If
II. If
III. If
Choose one answer.
|
a. I only |
||
|
b. I and II only |
||
|
c. I and III only |
||
|
d. I, II, and III |
Question 17
Suppose that 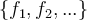 is an orthogonal basis for
is an orthogonal basis for 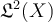 . Which of the following statements is false? (In what follows,
. Which of the following statements is false? (In what follows, 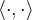 stands for the inner product on
stands for the inner product on 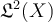 and
and 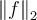 is the standard
is the standard 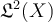 norm.)
norm.)
Choose one answer.
|
a. |
||
|
b. |
||
|
c. For all |
||
|
d. |
Question 18
Suppose that 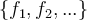 is an orthonormal basis for
is an orthonormal basis for 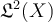 . Which of the following statements is true? (In what follows,
. Which of the following statements is true? (In what follows, 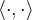 stands for the inner product on
stands for the inner product on 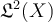 and
and 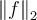 is the standard
is the standard 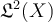 norm.)
norm.)
I.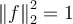 for any
for any 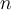 .
.
II.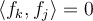 , for all
, for all 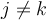 .
.
III.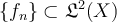
I.
II.
III.
Choose one answer.
|
a. I, II, and III |
||
|
b. I and II only |
||
|
c. I and III only |
||
|
d. II and III only |
Question 19
Complete the following statement. A linear operator 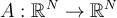 is self-adjoint, if and only if
is self-adjoint, if and only if 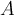 is:
is:
Choose one answer.
|
a. bounded. |
||
|
b. symmetric. |
||
|
c. continuous. |
||
|
d. normal. |
Question 20
If 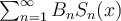 is the Fourier sine series of
is the Fourier sine series of 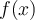 on
on 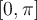 , which of the following statements must be true?
, which of the following statements must be true?
I. The graphs of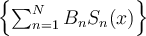 better approximate the function
better approximate the function  at points of continuity in
at points of continuity in 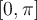 as
as 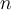 gets larger.
gets larger.
II.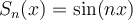 , for any
, for any 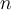 .
.
III.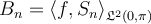 , for any
, for any 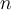 .
.
I. The graphs of
II.
III.
Choose one answer.
|
a. I, II, and III |
||
|
b. I and II only |
||
|
c. II and III only |
||
|
d. I only |
Question 21
Which of the following statements is false?
Choose one answer.
|
a. Every function f in |
||
|
b. There is a piecewise continuous function defined on |
||
|
c. |
||
|
d. If |
Question 22
If 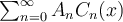 is the Fourier cosine series representation for
is the Fourier cosine series representation for  on
on 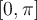 , then
, then 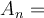 _________.
_________.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 23
Which of the following is true concerning the vector field 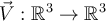 defined by
defined by 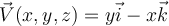 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 24
Suppose that
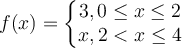
Which of the following is a correct characterization of the Fourier cosine series of at
at 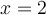 ?
?
Which of the following is a correct characterization of the Fourier cosine series of
Choose one answer.
|
a. It is not defined, because of the discontinuity of |
||
|
b. It converges to |
||
|
c. It converges to |
||
|
d. It does not converge because of the jump discontinuity. |
Question 25
If 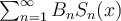 is the Fourier sine series for
is the Fourier sine series for  on
on 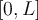 , which of the following is true?
, which of the following is true?
I.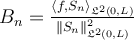
II.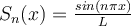
I.
II.
Choose one answer.
|
a. Neither I nor II |
||
|
b. I only |
||
|
c. II only |
||
|
d. Both I and II |
Question 26
Which of the following statements is true?
I. The Fourier sine series of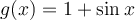 on
on 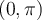 is simply
is simply 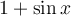 .
.
II. The Fourier cosine series of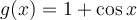 on
on 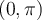 is simply
is simply 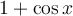 .
.
I. The Fourier sine series of
II. The Fourier cosine series of
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Neither I nor II |
||
|
d. Both I and II |
Question 27
Which of these formulas is equal to 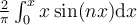 , where
, where 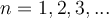 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 28
Which of the following is an accurately-stated consequence of Gibb’s phenomenon for a function 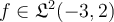 ?
?
Choose one answer.
|
a. The Fourier cosine series of |
||
|
b. The Fourier sine series of |
||
|
c. The Fourier sine series of |
||
|
d. The Fourier cosine series of |
Question 29
Suppose the real Fourier series for  on
on 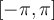 is given by
is given by
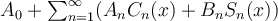 .
.
Which of the following statements is false?
I. If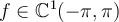 , then this series converges pointwise on
, then this series converges pointwise on 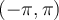 .
.
II.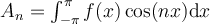
III. If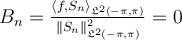 , for any
, for any 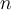 , then
, then  is an even function.
is an even function.
Which of the following statements is false?
I. If
II.
III. If
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. I and III only |
||
|
d. II and III only |
Question 30
Suppose 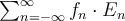 is the complex Fourier series representation of
is the complex Fourier series representation of  on
on 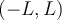 , and assume that
, and assume that 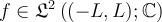 . Which of the following is false?
. Which of the following is false?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 31
Assume that the Fourier sine series representation of  is
is 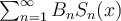 . Which of the following is the unique solution of the one dimensional heat equation
. Which of the following is the unique solution of the one dimensional heat equation 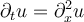 on
on 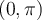 coupled with homogenous Dirichlet boundary conditions
coupled with homogenous Dirichlet boundary conditions 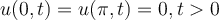 and initial condition
and initial condition 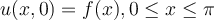 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 32
Assume that the Fourier sine series representation of f is 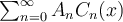 . Which of the following is the unique solution of the one dimensional heat equation
. Which of the following is the unique solution of the one dimensional heat equation 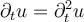 on
on 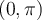 coupled with homogenous Neumann boundary conditions
coupled with homogenous Neumann boundary conditions 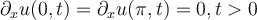 and initial condition
and initial condition 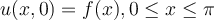 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 33
Let 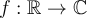 be defined by
be defined by 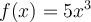 . Which of the following is the Fourier transform
. Which of the following is the Fourier transform 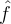 of
of  ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 34
Which of the following functions is harmonic in 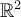 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 35
Suppose f and g are continuous and absolutely integrable on 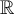 . Which of the following statements is true?
. Which of the following statements is true?
I.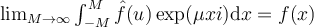
II.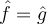 if and only if
if and only if 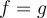 .
.
I.
II.
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Neither I nor II |
||
|
d. Both I and II |
Question 36
Suppose 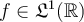 and its Fourier transform
and its Fourier transform 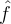 also belongs to
also belongs to 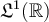 . Which of the following need NOT hold?
. Which of the following need NOT hold?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 37
Suppose 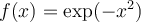 and denote its Fourier transform by
and denote its Fourier transform by 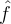 . Which of the following statements are true?
. Which of the following statements are true?
I.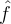 is continuous on
is continuous on  .
.
II.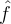 is bounded on
is bounded on 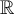 .
.
III.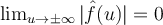 .
.
I.
II.
III.
Choose one answer.
|
a. I only |
||
|
b. I and III only |
||
|
c. II and III only |
||
|
d. I, II, and III |
Question 38
Suppose 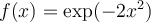 and
and 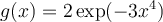 , and denote their Fourier transforms by
, and denote their Fourier transforms by 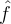 and
and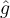 , respectively. Which of the following are accurate statements concerning the convolution
, respectively. Which of the following are accurate statements concerning the convolution ?
?
I. If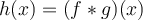 then
then 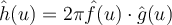 .
.
II.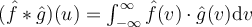
I. If
II.
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Neither I nor II |
||
|
d. Both I and II |
Question 39
Fill in the blank. Suppose that 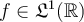 and define a function
and define a function 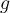 by
by 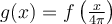 . Denote their Fourier transforms by
. Denote their Fourier transforms by 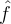 and
and 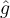 , respectively. For any
, respectively. For any 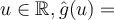 _______.
_______.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 40
Fill in the blank. Suppose that 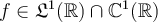 and define a function
and define a function 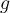 by
by 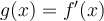 . Denote their Fourier transforms by
. Denote their Fourier transforms by 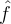 and
and 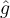 , respectively. Then,
, respectively. Then, 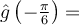 _________.
_________.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 41
Fill in the blank. Suppose that 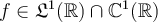 and define a function
and define a function 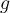 by
by 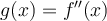 . Denote their Fourier transforms by
. Denote their Fourier transforms by 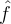 and
and 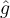 , respectively. Then,
, respectively. Then, 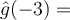 __________.
__________.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 42
Let 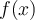 be a function. Which of the following descriptive statements regarding its Fourier transform
be a function. Which of the following descriptive statements regarding its Fourier transform 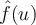 are correct?
are correct?
I. The Fourier transform converts differentiation in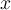 into multiplication in
into multiplication in 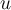 .
.
II. The smoothness of is closely related to the asymptotic decay rate of its Fourier transform
is closely related to the asymptotic decay rate of its Fourier transform 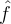 ?
?
III. The asymptotic decay rate of determines the smoothness of its Fourier transform.
determines the smoothness of its Fourier transform.
I. The Fourier transform converts differentiation in
II. The smoothness of
III. The asymptotic decay rate of
Choose one answer.
|
a. I only |
||
|
b. I and II only |
||
|
c. I and III only |
||
|
d. I, II, and III |
Question 43
Which of the following is the Fourier transform of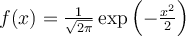 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 44
Which of the following is NOT equal to the Gauss-Weierstrass kernel 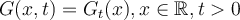 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 45
Define the operator 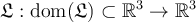 .
.
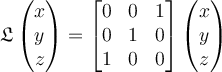 .
.
Which of the following is NOT a characteristic of the operator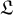 ?
?
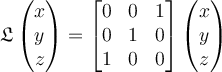 .
.Which of the following is NOT a characteristic of the operator
Choose one answer.
a. 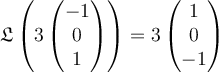 |
||
b. 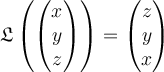 , for all , for all |
||
|
c. |
||
|
d. |
Question 46
Let 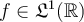 and
and 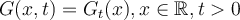 be the Gauss-Weierstrass kernel. Consider the one dimensional heat equation
be the Gauss-Weierstrass kernel. Consider the one dimensional heat equation 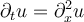 on
on 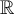 coupled with the initial condition
coupled with the initial condition 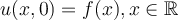 . Which of the following is the unique solution of this IVP?
. Which of the following is the unique solution of this IVP?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 47
Suppose that 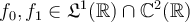 and denote their Fourier transforms by
and denote their Fourier transforms by 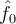 and
and 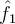 , respectively. Which of the following is the unique solution of the one dimensional wave equation
, respectively. Which of the following is the unique solution of the one dimensional wave equation 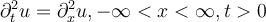 coupled with the initial conditions
coupled with the initial conditions 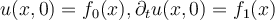 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 48
Suppose that 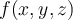 is a function of three variables,
is a function of three variables, 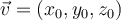 , and
, and 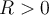 . Which of the following is the spherical average of
. Which of the following is the spherical average of  at
at 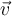 of radius
of radius 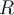 ? (Here,
? (Here, 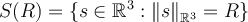 .)
.)
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 49
Let 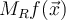 denote the spherical average of
denote the spherical average of  at
at 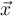 of radius
of radius 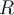 and let
and let 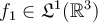 . Which of the following is the unique solution of the three-dimensional wave equation
. Which of the following is the unique solution of the three-dimensional wave equation 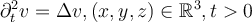 coupled with the initial conditions
coupled with the initial conditions 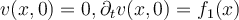 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 50
Assume that 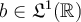 with Fourier transform
with Fourier transform 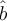 . Which of the following is the unique solution
. Which of the following is the unique solution 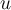 of the two-dimensional Laplace equation
of the two-dimensional Laplace equation 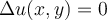 , where
, where 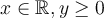 coupled with the boundary condition
coupled with the boundary condition 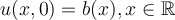 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 51
Let 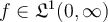 with Fourier cosine transform
with Fourier cosine transform 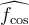 and Fourier sine transform
and Fourier sine transform 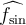 . Which of the following is the unique solution of the one dimensional heat equation
. Which of the following is the unique solution of the one dimensional heat equation 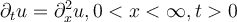 coupled with the initial condition
coupled with the initial condition 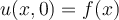 and boundary condition
and boundary condition 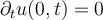 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 52
Suppose 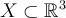 is a domain and
is a domain and 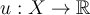 is a nonconstant harmonic function. Which of these is true?
is a nonconstant harmonic function. Which of these is true?
I.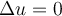 on
on 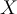 .
.
II.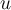 has no maximal points on the boundary of
has no maximal points on the boundary of 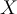 .
.
I.
II.
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Neither I nor II |
||
|
d. Both I and II |
Question 53
Which of the following is the d’Alembert solution of the one-dimensional wave equation 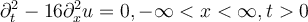 coupled with the initial conditions
coupled with the initial conditions 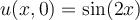 and
and 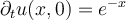 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 54
Let 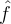 denote the Fourier transform of
denote the Fourier transform of  . Which of the following is false?
. Which of the following is false?
Choose one answer.
|
a. |
||
|
b. The inverse Fourier transform of |
||
|
c. |
||
|
d. |
Question 55
Let 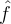 denote the Fourier transform of
denote the Fourier transform of  . Which of the following is false?
. Which of the following is false?
I.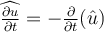
II.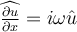
III.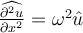
I.
II.
III.
Choose one answer.
|
a. I only |
||
|
b. III only |
||
|
c. I and II only |
||
|
d. II and III only |
Question 56
Which of the following statements is true?
Choose one answer.
|
a. The sum of two solutions of the PDE |
||
|
b. The PDE |
||
|
c. The 3-dimensional Laplace equation |
||
|
d. The Fokker-Plank equation |
Question 57
Let 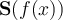 and
and 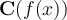 denote the Fourier sine and cosine transforms of
denote the Fourier sine and cosine transforms of  , respectively. Which of the following holds?
, respectively. Which of the following holds?
I.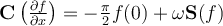
II.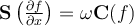
I.
II.
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Both I and II |
||
|
d. Neither I nor II |
Question 58
Which of the following PDEs are NOT evolution equations?
I.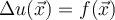
II.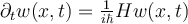
III.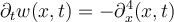
I.
II.
III.
Choose one answer.
|
a. Both II and III |
||
|
b. Both I and III |
||
|
c. I, II, and III |
||
|
d. I only |
Question 59
Assume 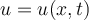 represents the temperature along a thin wire at position x at time t, where
represents the temperature along a thin wire at position x at time t, where 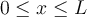 and
and 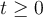 . Which of the following statements is false when viewed as a condition coupled with the heat equation
. Which of the following statements is false when viewed as a condition coupled with the heat equation 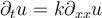 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 60
Which of the following statements is an accurate physical interpretation of a homogeneous Neumann boundary condition in the context of the heat equation?
Choose one answer.
|
a. The boundary is an imperfect conductor. |
||
|
b. The boundary is a permeable barrier to the flow of heat. |
||
|
c. No heat is crossing the boundary. |
||
|
d. The speed and direction of heat flow through the left boundary are positive. |
Question 61
Solve the following initial-value problem using the method of characteristics:
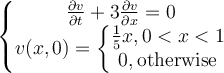
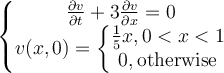
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 62
Solve the following initial-value problem using the method of characteristics:
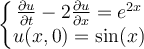
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 63
Solve the following initial-boundary value problem:
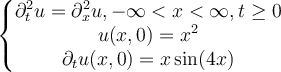
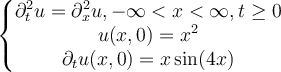
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 64
Solve the following boundary value problem:
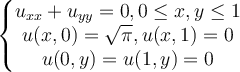
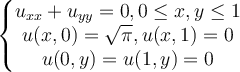
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 65
Determine the Fourier series representation for 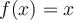 on
on 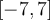 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 66
Determine the Fourier series representation for 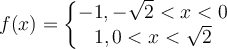 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 67
Consider the Laplace equation on a circle of radius a given by
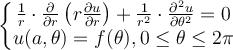
Which of the following system of ODEs in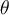 and
and 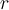 arises as part of the solution process when using separation of variables?
arises as part of the solution process when using separation of variables?
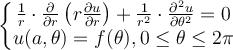
Which of the following system of ODEs in
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 68
Solve the following initial-value problem.
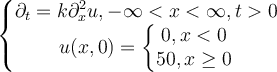
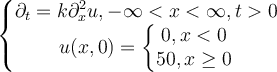
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 69
Solve the following boundary-value problem.
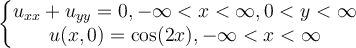
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question 70
Let 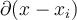 denote the Dirac delta function concentrated at
denote the Dirac delta function concentrated at 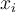 . How many of the following statements are true?
. How many of the following statements are true?
I.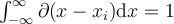
II.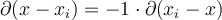
III.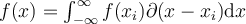 , for all functions
, for all functions 
IV.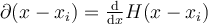 , where
, where 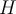 is the Heaviside function
is the Heaviside function
V.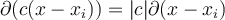 , where
, where 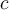 is a real constant
is a real constant
I.
II.
III.
IV.
V.
Choose one answer.
|
a. 0 |
||
|
b. 1 |
||
|
c. 3 |
||
|
d. 4 |
Question 71
Consider the following initial-boundary value problem:
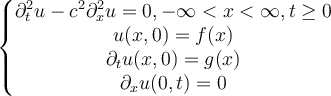
Which of the following statements is true regarding the solution u of this IBVP?
I.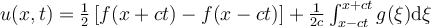 for all
for all 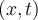 such that
such that 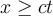
II.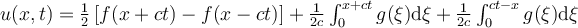 for all
for all 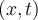 such that
such that 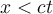
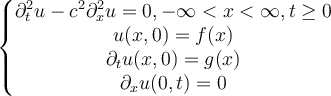
Which of the following statements is true regarding the solution u of this IBVP?
I.
II.
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Both I and II |
||
|
d. Neither I nor II |
Question 72
Consider the following initial-boundary value problem:
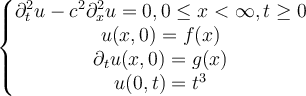
Which of the following statements is true regarding the solution u of this IBVP?
I.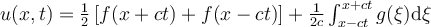 for all
for all 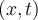 such that
such that 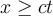
II.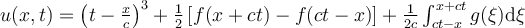 for all
for all 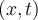 such that
such that 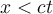
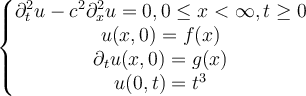
Which of the following statements is true regarding the solution u of this IBVP?
I.
II.
Choose one answer.
|
a. I only |
||
|
b. II only |
||
|
c. Both I and II |
||
|
d. Neither I nor II |