Suppose G is a group of order 21, and H is a proper subgroup of order 3. How many distinct left cosets of H are there?

Choose one answer.

	a. 18
	b. 24
	c. 7
	d. 3

Question 2

Suppose G is a finite group of order 56, and H and K are proper subgroups of G, such that K is also a proper subgroup of H. If [G:K] = 14 and [H:K] = 2, what would [G:H] have to be equal to?

Choose one answer.

	a. 7
	b. 12
	c. 24
	d. 1

Question 3

Let G be a group of order p⁴, where p is prime. Which of the following statements must be true?

Choose one answer.

	a. G is cyclic.
	b. G has a nontrivial center.
	c. G is isomorphic to S₄
	d. G has no proper subgroups.

Question 4

Let G be a group of order 125. What is true of G's center?

Choose one answer.

	a. G's center must be order 5 or 25.
	b. G has no trivial center.
	c. G is cyclic.
	d. G has no proper subgroups.

Question 5

Suppose G is a finite abelian group. Suppose the center of G has order 11. Then, which if the following must be true?

Choose one answer.

	a. G cannot be its own center.
	b. G cannot be cyclic.
	c. G must have order 11 or order 121.
	d. None of the above

Question 6

Let G be a finite group with proper subgroups H, J and K. Further, let K ⊂ J ⊂ H. If [G:H] = 5, [H:J] = 3 and [J:K] = 7, what is [G:K]?

Choose one answer.

	a. 15
	b. 7
	c. 1024
	d. 371

Question 7

Suppose G is a group of order 98. Which of the following statements must be true?

Choose one answer.

	a. G must contain a proper subgroup H of order 49.
	b. G must be abelian.
	c. G cannot contain a nontrivial center.
	d. G must be cyclic.

Question 8

Suppose G is a group with proper subgroups H and K. Further, suppose K ⊂ H and that K has 12 left cosets in G and K has 3 left cosets in H. How many left cosets in G does H have?

Choose one answer.

	a. 36
	b. 9
	c. 15
	d. 4

Question 9

Suppose that G is an abelian group of order 270. To which of the following is G isomorphic?

Choose one answer.

	a. Z₁₈XZ₁₅
	b. Z₁₀XZ₉XZ₃
	c. Z₂XZ₂₇XZ₅
	d. Z₆XZ₉XZ₅

Question 10

Suppose G is a finite subgroup of order 39. If H is a proper, nontrivial subgroup, what is the smallest order H might have?

Choose one answer.

	a. 3
	b. 13
	c. 39
	d. G cannot have a proper, nontrivial subgroup.

Question 11

Suppose G is a finite subgroup of order 39. If H is a proper, nontrivial subgroup, what is the largest order H might have?

Choose one answer.

	a. 3
	b. 13
	c. 39
	d. G cannot have a proper, nontrivial subgroup.

Question 12

Suppose we know that G is a group and that it has no trivial subgroups. Then, which of the following statements is true?

Choose one answer.

	a. G has a prime order.
	b. G can only be {e}.
	c. G can only be an infinite group.
	d. G cannot have cosets.

Question 13

G is a finite group with proper, nontrivial subgroups H and J. Which of the following statements must be true?

Choose one answer.

	a. The order of H ∩ J must divide the order of G.
	b. H ∪ J = G.
	c. H has no nontrivial subgroups.
	d. J only has a trivial subgroup if H has one.

Question 14

Let G be a finite group of order 63. If H and J are proper, nontrivial subgroups of G, H ≠ J, what is the largest order H ∩ J may have?

Choose one answer.

	a. 21
	b. 7
	c. 3
	d. 1

Question 15

Suppose G is some cyclic group order n. If we know for some a ∈ G that a⁵ = e and a¹¹ = e, then what is the smallest order G may take?

Choose one answer.

	a. 1
	b. 5
	c. 11
	d. 55

Question 16

Suppose G is an abelian group of order 270. Which of the following statements is false?

Choose one answer.

	a. G will not have a subgroup of order 15.
	b. G cannot have a subgroup of order 3.
	c. G may not have a subgroup of order 30.
	d. G may have a normal subgroup of order 27.

Question 17

Suppose G is some cyclic group of order 91. Let a ∈ G, such that aⁿ = e. What is the largest value n may take?

Choose one answer.

	a. 1
	b. 7
	c. 13
	d. 91

Question 18

Let G be a group and H be one of G's subgroups. If H has order 19 and has 5 left cosets in G, what is the order of G?

Choose one answer.

	a. 5
	b. 19
	c. 95
	d. 190

Question 19

Suppose K is the result of several intersections of proper subgroups of some finite abelian group G, with G having order 1024. What is true of K?

Choose one answer.

	a. K has to be {e}.
	b. K has to have an order of 2.
	c. K has to have an order of 2ⁿ, where n ≤ 10.
	d. K has to be G.

Question 20

Fill in the blank. Let G be a group G, and let H be a proper subgroup in G. If for all x, y ∈ G, and h ∈ H we know that xh = hy ∈ H implies that x = y, then ________________.

Choose one answer.

	a. G must be abelian
	b. H must be {e}
	c. H must be G
	d. H must be normal

Question 21

Suppose that we know some group G contains the elements {a, b, c, d, e}, where e is the identity. What is the largest subgroup of G?

Choose one answer.

	a. {e}
	b. {a, e}
	c. {a, c, e}
	d. G

Question 22

Suppose some subgroup H of G has order 5 and suppose H ≠ G. If G is abelian, what is the smallest order G may have?

Choose one answer.

	a. 5
	b. 25
	c. 125
	d. 625

Question 23

Suppose G is a finite group and for every a ∈ G, n ∈ Z, aⁿ = e. What has to be true about G?

Choose one answer.

	a. G has to have a prime order.
	b. G cannot be abelian.
	c. G has to have order of 1.
	d. G has to be empty.

Question 24

Let G have a center of order 7 and let the center have 12 left cosets in G. What must be true about G?

Choose one answer.

	a. G is not abelian.
	b. G has order 84.
	c. G may have subgroups of order 3 and 4.
	d. All of the above

Question 25

Suppose G = {a,b,c,d,e,f,g,h,i,j} is a group. What are the only possible orders of subgroups of G?

Choose one answer.

	a. 1
	b. 1,2
	c. 1,2,5
	d. 1,2,5,10

Question 26

Compute (5x² + 3x - 4) + (4x² - x + 9) in Z12.

Choose one answer.

	a. 20x⁴ + 7x³ + 42x² + 23x - 36
	b. 9x² + 2x + 5
	c. 8x⁴ + 7x³ + 6x² + 9x
	d. x² - 4x - 13

Question 27

Fill in the blank. If a commutative ring R has no zero divisors (that is, if ab = 0, then either a = 0 or b = 0), then R is also called a(n) ________________.

Choose one answer.

	a. Unique factorization ring
	b. Ideal
	c. Integral domain
	d. Module

Question 28

Let R be an integral domain and let 3, b be elements in R. If 3b = 0, then what might b equal?

Choose one answer.

	a. b might be equal to any multiple of 3.
	b. b must equal 0.
	c. b cannot be a multiple of 3.
	d. b must be the multiplicative inverse of 3.

Question 29

If f(x) is an irreducible polynomial, with f(x) | p(x)q(x), then which of the following is true?

Choose one answer.

	a. f(x) is a zero divisor.
	b. f(x) = either p(x) or q(x).
	c. f(x) \| p(x) or f(x) \| q(x)
	d. f(x) = p(x)q(x).

Question 30

Let F be a field and let a(x) = p(x)q(x) + r(x) have coefficients in F. Then, which of the following statements is true?

Choose one answer.

	a. r(x) must be the zero polynomial.
	b. deg r(x) must be less than deg q(x).
	c. r(x) must be irreducible.
	d. deg r(x) must be zero.

Question 31

Suppose f(x) is a polynomial with rational coefficients. If f(x) can be expressed as the product of two non-constant polynomials p and q, then what must be true of p and q?

Choose one answer.

	a. p and q cannot have the same degrees.
	b. p and q MUST have the same degrees.
	c. The degrees of p and q must be smaller than the degree of f.
	d. f must be a monic polynomial.

Question 32

If F is an integral domain, and f(x) is a polynomial with coefficients in F, then which of the following is true of f(x)?

Choose one answer.

	a. f(x) is irreducible.
	b. f(x) must have a unique factorization.
	c. f(x) is either irreducible or factorable.
	d. f(x) is a constant polynomial.

Question 33

If F is an integral domain and every polynomial with coefficients in F can be factored in distinct ways, then what is true of F?

Choose one answer.

	a. F is a unique factorization domain.
	b. F must be a field.
	c. F must be a module.
	d. F must be a commutative ring.

Question 34

If a ring R of square matrices under matrix addition and cross multiplication is isomorphic to a commutative ring, then what must be true?

Choose one answer.

	a. R must be a UFD.
	b. R must be of finite order.
	c. R must be a commutative ring.
	d. The image of R must be the set of rational numbers.

Question 35

Which of the following statements is true of a subring of a commutative ring?

Choose one answer.

	a. A subring of a commutative ring must itself be commutative.
	b. A subring of a commutative ring may not be commutative.
	c. A subring of a commutative ring may not be associative under multiplication.
	d. A subring of a commutative ring is always a prime ideal.

Question 36

Fill in the blank. Suppose R is a commutative ring such that for a, b, and c in R, ab = ac implies b = c. At the very least, R has to be a(n) _______________.

Choose one answer.

	a. UFD
	b. Field
	c. Prime ideal
	d. Integral domain

Question 37

Which of the following is true of a ring with a zero divisor?

Choose one answer.

	a. It can never be an integral domain.
	b. It may be an integral domain if it is commutative.
	c. It is a UFD.
	d. It is a prime ideal.

Question 38

B A field is a commutative division ring.

Choose one answer.

	a. A field has no zero divisors.
	b. A division ring has no unity.
	c. A division ring may have non-zero elements that have no inverses under multiplication.

Question 39

Fill in the blank. Let R be a Boolean ring. Then, for every a in R, a² = a. Then, R must be ________________.

Choose one answer.

	a. Finite
	b. A non-trivial ideal
	c. Commutative
	d. A field

Question 40

Suppose L is a lattice. Then, which of the following is true?

Choose one answer.

	a. Each element is divisible by all the elements less than itself.
	b. Each element is equal to all other elements in L.
	c. L has a partial order defined on it.
	d. L has to be a Boolean algebra.

Question 41

Which of the following best describes Boolean algebras?

Choose one answer.

	a. Boolean algebras are ring-like structures that form incomplete lattices.
	b. Boolean algebras are ring-like structures that have no zero elements.
	c. Boolean algebras are ring-like structures that use both set and logic operations.
	d. Boolean algebras are ring-like structures that have no unique upper and lower bounds.

Question 42

What does the following lattice best represent?

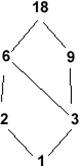
Choose one answer.

	a. A partial ordering of the unique divisors of 18
	b. A random walk between points 1 and 18
	c. A process map of steps in a program, where numbers represent called subroutines
	d. All of the above

Question 43

Boolean algebras are useful for their ability to do which of the following?

Choose one answer.

	a. Represent complex circuitry
	b. Assist in finding exploits in a computer network
	c. Represent physical security layouts
	d. Locate trends in a social network

Question 44

Which of the following terms is defined as a complemented, distributed lattice?

Choose one answer.

	a. A module
	b. A partially ordered set
	c. An invertible matrix
	d. A Boolean algebra

Question 45

If a polynomial of degree n is factorable, then what must be true of any factor?

Choose one answer.

	a. The degree of the factor must be less than n.
	b. The degree of the factor must be 0.
	c. The degree of the factor must be 1.
	d. The degree of the factor must divide n evenly.

Question 46

Let f be a polynomial with rational coefficients and let it be factorable into two polynomials p and q. If deg p(x) = j and deg q(x) = k, then what must the degree of f be?

Choose one answer.

	a. deg f(x) = 1.
	b. deg f(x) = 0.
	c. deg f(x) = jk.
	d. There is not enough information given to determine the answer.

Question 47

Fill in the blank. The property that says that if a, b are in some set R and (a,b), (b,a) are both in some relation, P implies that a = b is called the _______________ property.

Choose one answer.

	a. Transitive
	b. Reflexive
	c. Antisymetric
	d. Symmetric

Question 48

Let X = {1, 2, 3, 4, 6, 12, 24} be the set of divisors of 24, and let M = {2,3,4,6} be a proper subset of X. What is the least upper bound of M?

Choose one answer.

	a. 6
	b. 12
	c. 24
	d. There is no least upper bound.

Question 49

Fill in the blank. Suppose a lattice L has a largest element I and a smallest element O, and there exists binary operations ⋀ and ⋁ on the elements of L. If for every a in L, there exists an a' in L such that a ⋀ a' = O and a ⋁ a' = I, we say that L is _______________.

Choose one answer.

	a. Invertible
	b. Commutative
	c. Complemented
	d. Associative

Question 50

Which of the following is an example of Boolean algebra?

Choose one answer.

	a. Power set of some random set X
	b. Any finite group
	c. A group with a prime order
	d. Any commutative ring

Question 51

Fill in the blank. The _______________ of real numbers, denoted by Rⁿ, form a vector space over R.

Choose one answer.

	a. n-tuples
	b. n-dimensional arrays
	c. Power set of any n elements
	d. Set of all permutations of any n elements

Question 52

What is a vector space?

Choose one answer.

	a. A vector space is a non-abelian ring made up of n-tuples.
	b. A vector spaces is an abelian ring made up of n-tuples.
	c. A vector space is a non-abelian group extended by scalar multiplication.
	d. A vector spaces is an abelian group extended by scalar multiplication.

Question 53

Choose the best answer to fill in the blanks. A subset of a vector space is itself a vector space (called a subspace), if it is closed under _______________ multiplication and ______________ addition.

Choose one answer.

	a. Scalar, scalar
	b. Vector, vector
	c. Scalar, vector
	d. Vector, scalar

Question 54

A set of all linear combinations of some vector set V is called which of the following?

Choose one answer.

	a. V's combination class
	b. V's spanning set
	c. V's linear representation
	d. V's rank

Question 55

Fill in the blank. Let S be a set of vectors of some n-dimensional vector space V. If there exist scalars a₁ through a_n, such that a₁v₁ + … + a_nv_n = 0, but not all a's = 0, then S is said to be linearly _______________.

Choose one answer.

	a. Independent
	b. Combined
	c. Dependent
	d. Represented

Question 56

If S, a set of vectors of V, spans V, then S is said to be a _______________ of V.

Choose one answer.

	a. Representation
	b. Projection
	c. Basis
	d. Linear combination

Question 57

Fill in the blank. A mapping of a set V onto itself that changes the spanning set of V is called a change of _______________.

Choose one answer.

	a. Status
	b. Basis
	c. Identification
	d. Projection

Question 58

An nxn matrix M can only change a basis for an n-dimensional vector space if which of the following is true?

Choose one answer.

	a. M is nonsingular.
	b. M has a 0 determinant.
	c. M has rank less than n.
	d. M cannot be reduced to I by row operations.

Question 59

What is the product of a 5 X 3 matrix and a 3 X 4 matrix?

Choose one answer.

	a. A 3 X 3 matrix
	b. A 4 X 5 matrix
	c. A 15 X 12 matrix
	d. A 5 X 4 matrix

Question 60

A homomorphism between two vector spaces can always be represented by which of the following?

Choose one answer.

	a. A power set
	b. An abelian group
	c. A projection
	d. A matrix

Question 61

Fill in the blank. The rank of a matrix must be _______________ the rank of a map it represents.

Choose one answer.

	a. Less than
	b. Greater than
	c. Equal to
	d. At least one less than

Question 62

Which of the following can serve as a change of basis map for a n-dimensional space?

Choose one answer.

	a. A lattice of n partially ordered elements
	b. An invertible nxn matrix
	c. Any nxn matrix
	d. A pair of n-tuples

Question 63

Fill in the blank. The composition of linear maps is a ________________.

Choose one answer.

	a. Scalar
	b. Single vector
	c. Linear map
	d. Non-reversible projection

Question 64

Fill in the blank. The rank of a linear map is also the dimension of the map's _______________.

Choose one answer.

	a. Range space
	b. Null space
	c. Domain
	d. Projection space

Question 65

The dimension of a map's domain is equal to which of the following?

Choose one answer.

	a. The dimension of its rank
	b. The dimension of its nullity
	c. The sum of its rank and nullity
	d. None of the above

Question 66

Fill in the blank. The kernel of a linear map from vector space V to vector space W is the inverse image of W's ______________ vector.

Choose one answer.

	a. Unity
	b. Zero
	c. Largest
	d. Smallest

Question 67

Fill in the blank. The rank of a linear map is only equal to the dimension of the map's domain if the nullity of the map is _________________.

Choose one answer.

	a. Exactly zero
	b. Exactly one
	c. The multiplicative identity vector
	d. The rank of the map's codomain

Question 68

A linear map that is one-to-one must have which of the following?

Choose one answer.

	a. An invertible matrix
	b. A singular matrix
	c. A non-trivial nullity
	d. rank less than the domain

Question 69

Which of the following statements is true of a vector homomorphism?

Choose one answer.

	a. It is always onto and one-to-one.
	b. It is always onto but not necessarily one-to-one.
	c. It is always one-to-one but not necessarily onto.
	d. It is not always one-to-one nor onto.

Question 70

What is a vector homomorphism that is one-to-one and onto called?

Choose one answer.

	a. A linear map
	b. An isomorphism
	c. A projective map
	d. A change of representation

Question 71

An isomorphism maps a zero vector in one space to which of the following?

Choose one answer.

	a. A non-trivial kernel in another
	b. The zero vector of another
	c. The multiplicative identity of another
	d. The entire span of another

Question 72

An isomorphism preserves which of the following?

Choose one answer.

	a. Rank
	b. Identity
	c. Structure
	d. All of the above

Question 73

What is an isomorphism?

Choose one answer.

	a. An isomorphism is a type of equivalence relation.
	b. An isomorphism is a type of lattice.
	c. An isomorphism is a type of Boolean algebra.
	d. An isomorphism is a type of non-invertible function.

Question 74

What is an isomorphism from V onto itself called?

Choose one answer.

	a. A self-projection
	b. A reversible map
	c. A power map
	d. An automorphism

Question 75

Fill in the blank. Vector spaces are isomorphic if, and only if, the vector spaces have _________________.

Choose one answer.

	a. A linear map between them
	b. The same identity
	c. The same dimension
	d. The same kernel

Question 76

Fill in the blank. The set of all field automorphisms is a group under _________________.

Choose one answer.

	a. Set addition
	b. Composition of functions
	c. Translations of axes
	d. Matrix multiplication

Question 77

What is the set of all automorphisms of some field extension E of a field F that fix F elementwise called?

Choose one answer.

	a. The power set of E over F
	b. The Galois group of E over F
	c. The super group of E over F
	d. The kernel of E over F

Question 78

Fill in the blank. Complex conjugation (f: a + bi ⇒ a - bi) is a(n) ______________ of the complex numbers.

Choose one answer.

	a. Automorphism
	b. Bifurcation
	c. Splitting field
	d. Radial transformation

Question 79

If E is a field extension of F and f(x) is a polynomial in F|x|, then any automorphism in G(E/F) defines which of the following?

Choose one answer.

	a. A permutation of the roots of f(x) that lie in E
	b. A projection of the kernel of F in E
	c. A bijection from all elements in E to all elements in F
	d. None of the above

Question 80

Fill in the blank. Let E be an algebraic extension of a field F. If every irreducible polynomial in F|x| with a root in E has ALL its roots in E, then E is called a _________________ extension of F.

Choose one answer.

	a. Galois
	b. Projective
	c. Normal
	d. Power

Question 81

E being a finite, normal, separable extension of F is the same as saying which of the following?

Choose one answer.

	a. F is a splitting field over E of a separable polynomial.
	b. E is a Galois group of F.
	c. F is a Galois group of E.
	d. F = EG for some finite group of aut(E).

Question 82

Which of the following statements about the Galois group of E over F is true?

Choose one answer.

	a. Galois group of E over F is infinite.
	b. Galois group of E over F is abelian.
	c. Galois group of E over F has order equal to F.
	d. Galois group of E over F has a non-trivial center.

Question 83

What is a root of multiplicity of 1 called?

Choose one answer.

	a. Simple root
	b. Solitary root
	c. Unitary root
	d. Sole root

Question 84

Suppose E is a field extension of F and further suppose there existed an element a in E such that F(a) = E. What is such an element called?

Choose one answer.

	a. A simple element
	b. A solitary element
	c. A primitive element
	d. A unitary element

Question 85

Fill in the blank. If every element in E, which is an extension of F, is a root of a separable polynomial in F|x|, then E is called a ________________ extension of F.

Choose one answer.

	a. Separable
	b. Galois
	c. Simple
	d. Primitive

Question 86

Fill in the blank. A Galois group of E over F is a group of automorphisms of E that _______________ F elementwise (that is, f: Aut(E), such that f(a) = a for all a in F).

Choose one answer.

	a. Fixes
	b. Transposes
	c. Translates
	d. Rotates

Question 87

What is the set of all automorphisms of an extension field that fix elements of the extended field called?

Choose one answer.

	a. Commutative ring
	b. Abelian group
	c. Extended group
	d. Vector field

Question 88

Fill in the blank. Suppose E is a finite separable extension of a field F, then there must exist an element m in E, such that _______________.

Choose one answer.

	a. E = F(m)
	b. F = E(m)
	c. F = E
	d. m = e(m)

Question 89

Fill in the blank. If F is a field and G is a subgroup of Aut(F), then the set {a in F, such that f(a) = a for all f in G} is a ________________ of F.

Choose one answer.

	a. Galois group
	b. Communtator ring
	c. Subfield
	d. Noncommutative subring

Question 90

Fill in the blank. If f(x) in F|x| of degree n has n distinct roots in F's splitting field E, then f is ________________.

Choose one answer.

	a. Fixed
	b. Separable
	c. Simple
	d. Complex

Question 91

Suppose f(x) is irreducible over F. If F has characteristic 0, then which is true of f(x)?

Choose one answer.

	a. f(x) is separable.
	b. f(x) is a linear transformation.
	c. f(x) is the kernel of F.
	d. f(x) is an element of the automorphism of an extension field of F.

Question 92

Fill in the blank. A function f(x) is separable if it has n distinct roots in F's ________________ field E.

Choose one answer.

	a. Extension
	b. Splitting
	c. Fixed
	d. Embedded

Question 93

Which of the following of the automorphisms of F is a subfield of F?

Choose one answer.

	a. A general extension field
	b. A fixed field
	c. A power set
	d. A symmetric group

Question 94

Fill in the blank. A ______________ of a field F is a field E containing an element x, such that E = F(x).

Choose one answer.

	a. Separable extension
	b. Prime ideal
	c. Quotient ring
	d. Galois group

Question 95

Fill in the blank. The Galois group of some field E over F has a(n) _______________ center.

Choose one answer.

	a. Trivial
	b. Non-trivial
	c. Normal
	d. Extended

Question 96

Fill in the blank. A simple root of some polynomial has multiplicity of _______________.

Choose one answer.

	a. 0
	b. 1
	c. 2
	d. 3

Question 97

Fill in the blank. If a polynomial of degree n in F that has fewer than n roots in an extension field E, then E cannot be _________________.

Choose one answer.

	a. Simple
	b. Complex
	c. Separable
	d. F's extension field

Question 98

Fill in the blank. If an irreducible polynomial f has characteristic 0, then f is _______________.

Choose one answer.

	a. Monic
	b. Separable
	c. Simple
	d. Algebraic

Question 99

Fill in the blank. If some extension field E over F does not contain all the roots of F, then E cannot be ________________.

Choose one answer.

	a. Separable
	b. Primitive
	c. Solvable
	d. Monic

Question 100

A Galois group is a subgroup of which group of automorphisms?

Choose one answer.

	a. Permutation
	b. Power
	c. Partially ordered
	d. Separable