1
For which of the following sequences do we not know a closed-form formula?
Choose one answer.
| a. 1, 2, 3, 4, 5, 6, 7, 8, ... | ||
| b. 2, 3, 5, 7, 11, 13, 17, 19, ... | ||
| c. 1, 1, 2, 3, 5, 8, 13, 21, ... | ||
| d. 1, 3, 6, 10, 15, 21, 28, 36, ... |
Question
2
How many prime numbers are there, and why?
Choose one answer.
| a. Finitely many, because once you reach a certain size, every number factors into smaller primes. | ||
| b. We do not know, because computers aren't powerful enough to compute as large as we need. | ||
| c. Infinitely many, otherwise you could simply take the product of all of them and add one. | ||
| d. Infinitely many in theory, as you could theoretically extend the Sieve of Eratosthenes indefinitely. |
Question
3
How many prime numbers have integers as their square roots?
Choose one answer.
| a. 0 | ||
| b. 1 | ||
| c. 7 | ||
| d. infinitely many |
Question
4
Suppose we know that 3 divides a product 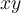 , but do
not know the precise values of
, but do
not know the precise values of 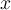 and
and 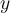 . Which statement must be true?
. Which statement must be true?
Choose one answer.
|
a. 3 must divide one of |
||
|
b. 3 divides neither |
||
|
c. 3 divides both |
||
|
d. We do not know if 3 divides |
Question
5
Suppose we know that 6 divides a product 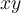 , but do
not know not the precise values of
, but do
not know not the precise values of 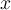 and
and 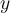 . Which statement must be true?
. Which statement must be true?
Choose one answer.
|
a. 6 must divide one of |
||
|
b. 6 divides neither |
||
|
c. 6 divides both |
||
|
d. We do not know if 6 divides |
Question
6
The 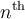 trapezoidal number is the number of pebbles you
get when arranged in a two-row trapezoid with
trapezoidal number is the number of pebbles you
get when arranged in a two-row trapezoid with 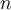 pebbles on the bottom row and
pebbles on the bottom row and 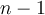 pebbles on the row
above. Find a concise formula for the
pebbles on the row
above. Find a concise formula for the 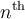 trapezoidal
number.
trapezoidal
number.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
7
What is the largest value that we must use to identify primes smaller than 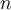 with the Sieve of Eratosthenes?
with the Sieve of Eratosthenes?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
8
Which of the following is not a property of the Fibonacci numbers 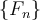 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
9
Which of the following number systems is not a ring?
Choose one answer.
| a. the natural numbers | ||
| b. the integers | ||
| c. the set of linear residues modulo 8 | ||
| d. the set of algebraic numbers |
Question
10
Which of the following orderings is not a linear ordering?
Choose one answer.
| a. ... < -1 < 0 < 1 < 2 < 3 < ... | ||
| b. ... > -1 > 0 > 1 > 2 > 3 > ... | ||
|
c. |
||
| d. {} < {a}, {b} < {a,b} |
Question
11
Why do prime numbers recur in nearly every number theoretic problem?
Choose one answer.
| a. Composite numbers can be rewritten as products of prime numbers. | ||
| b. Prime numbers have only a few properties, which are however very powerful. | ||
| c. It is harder to study prime numbers, but more rewarding. | ||
| d. It is easier to determine whether a number is prime. |
Question
12
Find the greatest common divisor of -2805 and 1287.
Choose one answer.
| a. 3 | ||
| b. 33 | ||
| c. 99 | ||
| d. 187 |
Question
13
Find the greatest common divisor of 34529 and 32923.
Choose one answer.
| a. 9 | ||
| b. 473 | ||
| c. 11 | ||
| d. 803 |
Question
14
For which integer values of 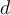 does the equation
does the equation
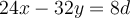 have integer solutions for
have integer solutions for 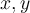 ?
?
Choose one answer.
|
a. no integer values of |
||
|
b. |
||
|
c. |
||
|
d. all integer values of |
Question
15
For which integer values of 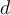 does the equation
does the equation
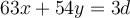 have integer solutions for
have integer solutions for 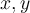 ?
?
Choose one answer.
|
a. no integer values of |
||
|
b. |
||
|
c. |
||
|
d. all integer values of |
Question
16
If the final steps of the Euclidean algorithm for 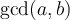 gives us the equations
gives us the equations 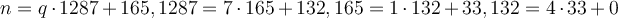 , then which of the
following would be a possible final result of finding Bezout's formula for
, then which of the
following would be a possible final result of finding Bezout's formula for 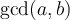 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
17
If the final steps of the Euclidean algorithm for 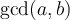 gives us the equations
gives us the equations 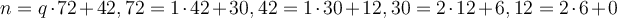 , then which of the
following would be a result of the first few steps towards acquiring Bezout's formula for
, then which of the
following would be a result of the first few steps towards acquiring Bezout's formula for 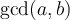 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
18
Suppose 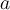 divides
divides 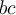 and
and 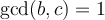 . What can we say about
. What can we say about 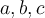 ?
?
Choose one answer.
|
a. |
||
|
b. We can find integers |
||
|
c. |
||
|
d. |
Question
19
Suppose 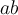 divides
divides 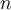 , but
, but 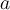 does not divide
does not divide 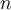 . What relationship can we establish between
. What relationship can we establish between 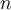 and
and 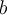 ?
?
Choose one answer.
| a. no relationship without more information | ||
|
b. |
||
|
c. |
||
|
d. |
Question
20
Suppose 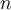 divides
divides 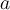 and
and 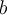 , while
, while 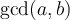 divides
divides 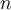 . What relationship can we establish between
. What relationship can we establish between 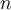 and
and 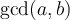 ?
?
Choose one answer.
|
a. only that |
||
|
b. that |
||
|
c. that |
||
|
d. that |
Question
21
Suppose 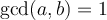 . Which integers
. Which integers 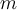 can be expressed in the form
can be expressed in the form 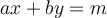 , where
, where 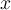 and
and 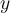 are integers?
are integers?
Choose one answer.
| a. all integers | ||
|
b. multiples of |
||
|
c. multiples of |
||
|
d. multiples of |
Question
22
Suppose 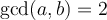 . Which integers
. Which integers 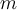 can be expressed in the form
can be expressed in the form 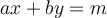 , where
, where 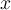 and
and 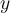 are integers?
are integers?
Choose one answer.
| a. all integers | ||
| b. even integers | ||
| c. odd integers | ||
|
d. multiples of |
Question
23
What relationship can we establish for 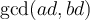 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. no relationship without more information |
Question
24
Which of the following Diophantine equations has a solution?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
25
Which of the following integer sequences is not guaranteed to have infinitely many primes?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
26
You want to find the gcd of a 15-digit number and a 20-digit number. How many divisions will it take to compute the gcd using the Euclidean algorithm?
Choose one answer.
| a. at most 75 | ||
| b. at most 100 | ||
| c. at most 175 | ||
| d. at most 35 |
Question
27
A simultaneous solution exists for the two linear congruences listed below. What third congruence could we add, and still obtain a solution?
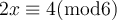
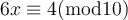
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
28
A simultaneous solution exists for the two linear congruences listed below. What third congruence could we add, and still obtain a solution?
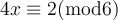
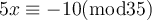
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
29
Find a simultaneous solution to the following system of linear congruences.
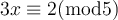
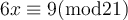
Choose one answer.
| a. 4 | ||
| b. 6 | ||
| c. 19 | ||
| d. 24 |
Question
30
Find a simultaneous solution to the following system of linear congruences.
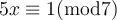
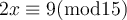
Choose one answer.
| a. 75 | ||
| b. 87 | ||
| c. 105 | ||
| d. no solution |
Question
31
Suppose a 7-digit number has digits 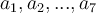 (left to
right). Which rule will allow us to check if the number is divisible by 12?
(left to
right). Which rule will allow us to check if the number is divisible by 12?
Choose one answer.
| a. The number is divisible by both 2 and 3. | ||
|
b. The sum |
||
|
c. The sum |
||
| d. There is no such rule. |
Question
32
Suppose a 7-digit number has digits 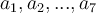 (left to
right). Why can we check if
(left to
right). Why can we check if 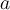 is divisible by 7 by
checking whether
is divisible by 7 by
checking whether 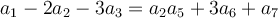 ?
?
Choose one answer.
| a. You can always check divisibility by rotating through positive and negative remainders. | ||
|
b. The coefficient of each |
||
|
c. You can always check divisibility by |
||
| d. This is one of those random coincidences in mathematics that you simply have to accept. |
Question
33
What is the multiplicative inverse of 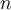 , modulo
, modulo
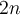 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There is none. |
Question
34
What is the multiplicative inverse of 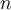 , modulo 23?
, modulo 23?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
| d. There is none. |
Question
35
Which of the following congruences has a solution?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
36
Which of the following statements about congruence is not always true?
Choose one answer.
|
a. If |
||
|
b. If |
||
|
c. If |
||
|
d. If |
Question
37
Which of the following statements about congruence is not always true?
Choose one answer.
|
a. If |
||
|
b. If |
||
|
c. If |
||
|
d. If |
Question
38
Compute the product of 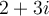 and
and 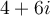 .
.
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
39
Essentially, what property of 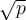 , where
, where 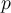 is prime, makes it irrational?
is prime, makes it irrational?
Choose one answer.
| a. Writing it as a ratio of two integers leads to a contradiction. | ||
| b. Its decimal expansion is infinite, but repeating. | ||
| c. Its decimal expansion is infinite, with factorial zeros. | ||
| d. Writing it as a ratio of two algebraic numbers leads to a contradiction. |
Question
40
Essentially, what property of Liouville's number makes it transcendental?
Choose one answer.
| a. Its decimal expansion is finite. | ||
| b. Its decimal expansion is infinite, but repeats. | ||
| c. Its decimal expansion is infinite, and does not repeat. | ||
| d. Its decimal expansion is infinite, with factorial zeros. |
Question
41
What is the geometric effect of multiplying a Gaussian integer 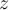 by
by  ?
?
Choose one answer.
|
a. Rescaling the vector that represents |
||
|
b. Reversing the vector that represents |
||
|
c. Rotating the vector that represents |
||
|
d. Shifting the vector that represents |
Question
42
What is the smallest ring that contains all solutions to linear integer equations 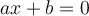 , given that
, given that 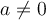 ?
?
Choose one answer.
| a. the integers | ||
| b. the rational numbers | ||
| c. the algebraic numbers | ||
| d. the real numbers |
Question
43
Which of the following numbers is algebraic and irrational?
Choose one answer.
| a. Liouville's number | ||
|
b. |
||
|
c. |
||
|
d. |
Question
44
Which of the following rings contains all algebraic roots of positive integers?
Choose one answer.
| a. the rational numbers | ||
| b. the algebraic numbers | ||
| c. the integers | ||
| d. any finite field |
Question
45
Which of the following rings does not satisfy the zero product property?
Choose one answer.
| a. the integers | ||
| b. the Gaussian integers | ||
| c. the set of linear residues modulo -5 | ||
| d. the set of linear residues modulo 8 |
Question
46
Find the continued fraction expansion for 3/5.
Choose one answer.
| a. [0;1,1,2] | ||
| b. [2;1,1] | ||
| c. [3;5] | ||
| d. [0;3,5] |
Question
47
What is the correct continued fraction expansion for 5/3?
Choose one answer.
| a. [1;1,1] | ||
| b. [1;1,2] | ||
| c. [1;2,3] | ||
| d. [5;3] |
Question
48
Which continued fraction is the only possible candidate for the cube root of a prime number?
Choose one answer.
| a. [2;1,5,2,2,7,1,16,4,1,8,10,...] | ||
| b. [2;1,5,2,2,7] | ||
| c. [2;1,5,2,2,7,1,5,2,2,7,...] | ||
| d. [2;0] |
Question
49
Which continued fraction is the only possible candidate for the square root of a prime number?
Choose one answer.
| a. [4;1,3,1,8] | ||
| b. [4;0] | ||
| c. [4;1,3,1,8,1,3,1,8,...] | ||
| d. [4;1,3,1,8,1,4,1,16,...] |
Question
50
Which of the following continued fractions is rational, but not integer?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
51
Which of the following continued fractions is rational?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
52
According to Fermat, which of the following is a good candidate for a large prime number?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
53
According to Mersenne, which of the following is a good candidate for a large prime number?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. |
||
|
d. |
Question
54
Evaluate 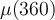 .
.
Choose one answer.
| a. -1 | ||
| b. 0 | ||
| c. 1 | ||
| d. undefined |
Question
55
Evaluate 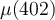 .
.
Choose one answer.
| a. -1 | ||
| b. 0 | ||
| c. 1 | ||
| d. undefined |
Question
56
Evaluate 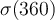 .
.
Choose one answer.
| a. 361 | ||
| b. 702 | ||
| c. 1170 | ||
| d. 2592 |
Question
57
Evaluate 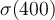 .
.
Choose one answer.
| a. 117 | ||
| b. 401 | ||
| c. 1170 | ||
| d. 2916 |
Question
58
Evaluate 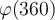 .
.
Choose one answer.
| a. 24 | ||
| b. 96 | ||
| c. 120 | ||
| d. 300 |
Question
59
Evaluate 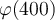 .
.
Choose one answer.
| a. 16 | ||
| b. 25 | ||
| c. 160 | ||
| d. 200 |
Question
60
In the RSA algorithm, what property of the modulus 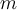 helps ensure the algorithm's correctness?
helps ensure the algorithm's correctness?
Choose one answer.
|
a. It is very difficult to factor |
||
|
b. Most numbers smaller than |
||
|
c. Computing exponents modulo |
||
|
d. Bezout's formula guarantees an inverse modulo |
Question
61
The RSA encryption scheme would be in danger if we could only find an "easy" method to perform which of the following problems?
Choose one answer.
| a. compute large primes | ||
| b. compute large exponents modulo a prime | ||
| c. compute the greatest common divisor | ||
| d. factor large integers |
Question
62
Use Euler's formula to solve 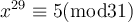 .
.
Choose one answer.
| a. 1 | ||
| b. 5 | ||
| c. 25 | ||
| d. No solution |
Question
63
Use Euler's formula to solve 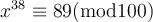 .
.
Choose one answer.
| a. 1 and -1 | ||
| b. 3 and -3 | ||
| c. 9 | ||
| d. No solution |
Question
64
We want to encrypt the message, EU LE RR OX, using the RSA algorithm. For our modulus, we will use 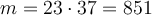 . The public key is 31. Find the private key.
. The public key is 31. Find the private key.
Choose one answer.
| a. 302 | ||
| b. 511 | ||
| c. 792 | ||
| d. 851 |
Question
65
What class of number is useful for computing perfect numbers?
Choose one answer.
| a. Fibonacci numbers | ||
| b. the Golden ratio | ||
| c. Mersenne primes | ||
| d. Fermat primes |
Question
66
Which of the following is always true for a multiplicative function 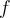 ?
?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. If |
||
|
d. If |
Question
67
Which of the following is not always true for a multiplicative function f?
Choose one answer.
|
a. |
||
|
b. |
||
|
c. If |
||
|
d. If |
Question
68
Which of the following is not an aspect of the RSA encryption scheme?
Choose one answer.
| a. The communicating parties exchange encryption and decryption keys. | ||
| b. The communicating parties build large prime numbers. | ||
| c. The communicating parties perform exponentiation modulo a large composite number. | ||
| d. The communicating parties would be in danger if integer factorization were "easy". |
Question
69
Which of the following numbers is perfect?
Choose one answer.
| a. 2 | ||
| b. 8 | ||
| c. 102 | ||
| d. 496 |
Question
70
Which of the following numbers is very closely related to discovering perfect numbers?
Choose one answer.
| a. Composite numbers | ||
| b. Fermat numbers | ||
| c. Fibonacci numbers | ||
| d. Mersenne numbers |