1
Complete each statement on different types of mappings with the correct characteristic.
|
To show that two sets |
||
|
If |
||
|
If a function |
Question
2
Match the following sequences with their limits.
|
The value of |
||
|
The value of |
Question
3
Suppose 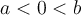 . If
. If 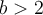 , which of the following statements is true?
, which of the following statements is true?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
4
Suppose that 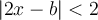 and
and 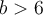 . What is the most one can say about
. What is the most one can say about 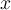 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
5
To show that for every 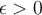 , there exists an
, there exists an
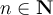 such that
such that 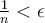 , one appeals to which of the following?
, one appeals to which of the following?
Choose one answer.
| A. The Archimedean Property | ||
| B. The Well-Ordering Principle | ||
| C. The completeness of the real numbers | ||
| D. The Supremum Property | ||
| E. The Axiom of Choice |
Question
6
A positive sequence may not be bounded under which circumstance?
Choose one answer.
| A. It is Cauchy. | ||
| B. It contains a convergent subsequence. | ||
| C. It is convergent. | ||
| D. It is nonincreasing. | ||
|
E. Its |
Question
7
Suppose that 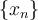 is a Cauchy sequence. Then which of
the following must be true?
is a Cauchy sequence. Then which of
the following must be true?
Choose one answer.
|
A. For every |
||
|
B. For some |
||
|
C. For every |
||
|
D. For some |
||
|
E. For every |
Question
8
Suppose that 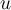 and
and 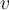 are elements of a real inner product space
are elements of a real inner product space 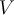 such that
such that 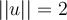 and
and 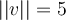 . What can we say about
. What can we say about 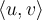 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
9
Which of the following is NOT a closed set in 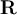 with
respect to the Euclidean metric?
with
respect to the Euclidean metric?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
10
Suppose 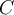 is a compact subset of
is a compact subset of 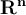 . Which of the following is false?
. Which of the following is false?
Choose one answer.
|
A. There exists |
||
|
B. Every sequence |
||
|
C. Every sequence |
||
|
D. |
||
|
E. If |
Question
11
Suppose 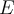 is a subset of a complete metric space
is a subset of a complete metric space
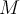 . Which of the following is most accurate?
. Which of the following is most accurate?
Choose one answer.
|
A. In order for every sequence in |
||
|
B. In order for every sequence in |
||
|
C. In order for every sequence in |
||
|
D. In order for every sequence in |
||
|
E. If |
Question
12
A metric space 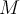 is complete under which
condition?
is complete under which
condition?
Choose one answer.
|
A. If every convergent sequence in |
||
|
B. If every Cauchy sequence in |
||
|
C. If every bounded sequence in |
||
|
D. If every sequentially continuous function on |
||
|
E. If every open cover of |
Question
13
Which of the following functions contradicts the statement that inverse images of connected sets under continuous maps are connected?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
14
Suppose that 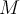 is a complete metric space, and let
is a complete metric space, and let
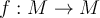 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. In order for |
||
|
B. In order for |
||
|
C. In order for |
||
|
D. In order for |
||
| E. None of the above |
Question
15
Let 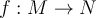 be a function between two metric spaces, let
be a function between two metric spaces, let
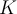 be a compact subset of
be a compact subset of 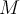 , and let
, and let 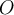 be an open subset of
be an open subset of 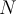 . Which of the following would NOT preclude the continuity of
. Which of the following would NOT preclude the continuity of
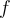 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. There exists a sequence |
||
|
D. There exists a point |
||
|
E. |
Question
16
Let ![]() be a sequence of functions with
be a sequence of functions with
![]() . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. In order for |
||
|
B. In order for |
||
|
C. In order for |
||
|
D. In order for |
||
|
E. If for every subsequence |
Question
17
Let 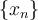 be a sequence in
be a sequence in 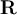 . Which of the following is NOT sufficient to guarantee that
. Which of the following is NOT sufficient to guarantee that 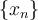 is convergent?
is convergent?
Choose one answer.
|
A. For every |
||
|
B. There exists |
||
|
C. There exists |
||
|
D. There exists |
||
|
E. There exists |
Question
18
Recall that a set 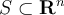 is convex if and only if for all
is convex if and only if for all
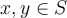 ,
, 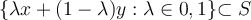 . Suppose that
. Suppose that 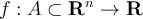 is differentiable and that for some
is differentiable and that for some 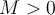 ,
, 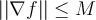 for all
for all 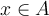 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. In order to have |
||
|
B. In order to have |
||
|
C. In order to have |
||
|
D. In order to have |
||
|
E. If |
Question
19
Suppose a set 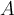 is a dense subset of another set
is a dense subset of another set
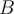 and that both are subsets of a metric space
and that both are subsets of a metric space
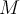 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. If |
||
|
B. If |
||
|
C. If |
||
|
D. If |
||
|
E. If |
Question
20
Let 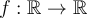 be continuously differentiable and satisfying,
for all
be continuously differentiable and satisfying,
for all 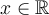 , the inequality
, the inequality 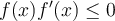 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. If for some |
||
|
B. |
||
|
C. The function |
||
|
D. If |
||
| E. Both options A and B are correct. |
Question
21
Let 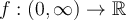 be differentiable and let
be differentiable and let 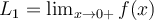 and
and 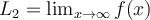 (in particular these limits exist). Which of the following implies the
existence of
(in particular these limits exist). Which of the following implies the
existence of 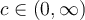 for which
for which 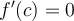 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of the above. |
Question
22
What does it mean to say that a function 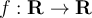 is
differentiable on its domain with derivative
is
differentiable on its domain with derivative 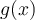 ?
?
Choose one answer.
|
A. For all |
||
|
B. For all |
||
|
C. Given |
||
|
D. There exists |
||
|
E. For all |
Question
23
Which of the following defines what it means for a sequence 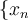 of positive numbers in
of positive numbers in 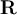 to be properly
divergent?
to be properly
divergent?
Choose one answer.
|
A. For every |
||
|
B. There exists some |
||
|
C. For every |
||
|
D. For every |
||
|
E. There exists a natural number |
Question
24
Given a function 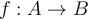 , and two subsets
, and two subsets 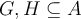 , what does one mean by
, what does one mean by 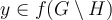 ?
?
Choose one answer.
|
A. |
||
|
B. There is no element |
||
|
C. |
||
|
D. There is an element |
||
|
E. There are elements |
Question
25
Let 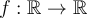 be differentiable and define
be differentiable and define 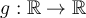 by the formula
by the formula 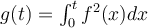 . Which of the following is the value of
. Which of the following is the value of 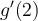 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of the above. |
Question
26
Suppose that 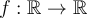 is continuous on
is continuous on 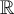 . Let
. Let 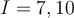 . Which of the following may be false?
. Which of the following may be false?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
27
Consider the following (false) claim and "proof;" find the incorrect step. Claim: All positive integers are equal. Proof:
1. It suffices to show that for any two positive integers, A and B, A = B.
2. Further, it suffices to show that for all N > 0, if A and B are positive integers which satisfy MAX(A, B) = N, then A = B.
3. (Base Case) If N = 1, then A and B, being positive integers, must both be 1. So A = B.
4. (Induction Step) Assume that the theorem is true for some value k. Take positive integers A and B with MAX(A, B) = k+1. Then, MAX((A-1), (B-1)) = k.
5. Therefore, by induction, (A-1) = (B-1). Consequently, A = B. Hence, A = B for all positive integers A and B by induction. Q.E.D.
1. It suffices to show that for any two positive integers, A and B, A = B.
2. Further, it suffices to show that for all N > 0, if A and B are positive integers which satisfy MAX(A, B) = N, then A = B.
3. (Base Case) If N = 1, then A and B, being positive integers, must both be 1. So A = B.
4. (Induction Step) Assume that the theorem is true for some value k. Take positive integers A and B with MAX(A, B) = k+1. Then, MAX((A-1), (B-1)) = k.
5. Therefore, by induction, (A-1) = (B-1). Consequently, A = B. Hence, A = B for all positive integers A and B by induction. Q.E.D.
Choose one answer.
| A. Step 1 | ||
| B. Step 2 | ||
| C. Step 3 | ||
| D. Step 4 | ||
| E. Step 5 |
Question
28
If 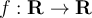 is a continuous function, and
is a continuous function, and 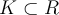 is compact, which of the following is true?
is compact, which of the following is true?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of the above |
Question
29
Suppose that a function 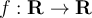 is monotone. Recall that
is monotone. Recall that
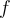 has the Darboux property on a set
has the Darboux property on a set 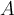 , if and only if given any
, if and only if given any 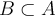 , for any
, for any 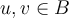 ,
, 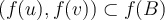 . Let
. Let 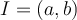 be an interval. Which of the following is true?
be an interval. Which of the following is true?
Choose one answer.
|
A. If |
||
|
B. If |
||
|
C. If |
||
|
D. If |
||
|
E. If |
Question
30
Consider a sequence 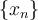 . What does it mean to say that
. What does it mean to say that
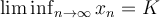 ?
?
Choose one answer.
|
A. As |
||
|
B. As |
||
|
C. As |
||
|
D. |
||
|
E. |
Question
31
Suppose that 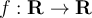 is monotone increasing. Which of the
following is false?
is monotone increasing. Which of the
following is false?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
32
Which of the following is NOT a norm on the set of continuous functions on 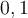 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
33
Which of the following is NOT sufficient to imply that a subset 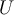 of a metric space
of a metric space 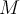 is open?
is open?
Choose one answer.
|
A. |
||
|
B. The intersection of |
||
|
C. For every point |
||
|
D. |
||
|
E. |
Question
34
A set 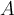 is a perfect set if it is closed and if every
element of
is a perfect set if it is closed and if every
element of 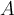 is an accumulation point. Which of the
following is true?
is an accumulation point. Which of the
following is true?
Choose one answer.
| A. Every compact set is perfect. | ||
| B. Every closed, unbounded set is perfect. | ||
| C. Every closed set is compact, perfect, or both. | ||
| D. Every perfect set is uncountable. | ||
| E. Every perfect set is bounded. |
Question
35
A set 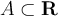 is said to be relatively compact if
is said to be relatively compact if
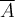 is compact. Given such a set
is compact. Given such a set 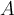 and a function,
and a function, 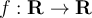 , which of the following is false?
, which of the following is false?
Choose one answer.
|
A. Every sequence in |
||
|
B. |
||
|
C. If |
||
|
D. If |
||
|
E. If |
Question
36
Suppose 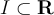 , where
, where 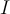 is an interval. Let
is an interval. Let 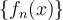 be a sequence of functions which converges pointwise to
be a sequence of functions which converges pointwise to 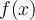 on
on 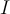 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. If each |
||
|
B. If each |
||
|
C. If each |
||
|
D. If the convergence of |
||
|
E. If the convergence of |
Question
37
Which of the following is sufficient to imply that a series 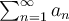 converges?
converges?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. The sequence |
Question
38
Consider two subsets 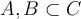 . Recall that the symmetric
difference of two sets
. Recall that the symmetric
difference of two sets 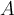 and
and 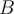 is
is 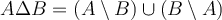 . What is the complement of this set in
. What is the complement of this set in 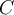 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
39
Let 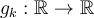 be a sequence of continuously differentiable
functions which converges uniformly on
be a sequence of continuously differentiable
functions which converges uniformly on 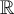 to the
function
to the
function 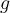 . Which of the following may be false?
. Which of the following may be false?
Choose one answer.
|
A. |
||
|
B. The sequence |
||
|
C. |
||
|
D. For all subsets |
||
|
E. |
Question
40
The Rational Numbers have the same cardinality as which of the following?
Choose one answer.
| A. The Real Numbers | ||
| B. The Irrational Numbers | ||
| C. The Transcendental Numbers | ||
| D. The Natural Numbers | ||
| E. The 5th roots of unity |
Question
41
Which of the following functions is NOT uniformly continuous on its domain?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
42
Suppose a function 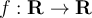 is uniformly continuous. Then,
which of the following is true?
is uniformly continuous. Then,
which of the following is true?
Choose one answer.
|
A. For every |
||
|
B. For every |
||
|
C. For every |
||
|
D. For every |
||
|
E. For every |
Question
43
Consider a sequence of functions 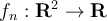 , which are
contraction mappings, i.e. for all
, which are
contraction mappings, i.e. for all 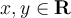 and for all
and for all
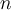 ,
, 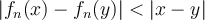 . Let
. Let 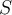 be an open, connected subset of
be an open, connected subset of 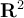 . Suppose that
. Suppose that 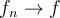 uniformly on S and
uniformly on S and 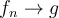 pointwise on
pointwise on  . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. In order for |
||
|
B. In order for |
||
|
C. In order for |
||
|
D. In order for |
||
|
E. If |
Question
44
Suppose a sequence of functions 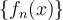 (with
(with 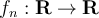 for each
for each 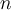 ) converges uniformly to a function
) converges uniformly to a function 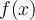 . Then, which of the following is true?
. Then, which of the following is true?
Choose one answer.
|
A. For every |
||
|
B. For every |
||
|
C. For every |
||
|
D. For some small |
||
|
E. For every |
Question
45
For each of the following sets consider it with its natural notion of addition and scalar multiplication with a rational number. Which of the following is
NOT a vector space over the field of rational numbers?
Choose one answer.
| A. The set of matrices with rational elements. | ||
|
B. The set of functions that are continuous on the closed interval |
||
| C. The set of real numbers. | ||
| D. The set of polynomials of degree less than or equal to five with rational coefficients. | ||
| E. The set of nonsingular matrices over the field of rational numbers |
Question
46
The well-ordering principle of the natural numbers asserts which of the following?
Choose one answer.
| A. Every nonempty set of positive integers contains a smallest element. | ||
|
B. If |
||
|
C. If |
||
| D. The natural numbers are unbounded. | ||
| E. The rational numbers are countable. |
Question
47
Simplified, 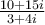 can be expressed as
can be expressed as 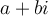 . What is
. What is 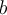 ?
?
Answer:
Question
48
What is the infimum of the set 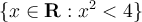 ?
?
Answer:
Question
49
Consider the line passing through the points 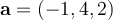 and
and
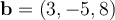 . Consider a point
. Consider a point 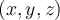 on the line. If
on the line. If 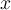 is given parametrically by
is given parametrically by 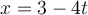 and
and 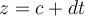 , what is
, what is 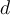 ?
?
Answer:
Question
50
Let 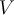 be an inner product space. What is
be an inner product space. What is 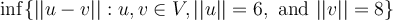 ?
?
Answer:
Question
51
Consider the plane normal to the vector 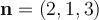 which
passes through the point
which
passes through the point 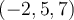 . An equation describing
all points
. An equation describing
all points 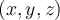 in the plane of the plane is
in the plane of the plane is
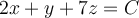 . What is the value of
. What is the value of 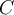 ?
?
Answer:
Question
52
True or False: The countable union of closed sets is closed.
Answer:
True False
Question
53
True or False: If 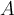 and
and 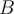 are subsets of a metric space
are subsets of a metric space 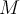 , and
, and 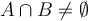 , then
, then 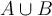 is connected.
is connected.
Answer:
True False
Question
54
True or False: If 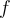 is a continuous, one-to-one map
between metric spaces, then
is a continuous, one-to-one map
between metric spaces, then 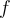 has a continuous
inverse.
has a continuous
inverse.
Answer:
True False
Question
55
True or False: If 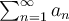 is a convergent, real series
which is not absolutely convergent, then for every
is a convergent, real series
which is not absolutely convergent, then for every 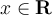 ,
there exists a rearrangement
,
there exists a rearrangement 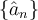 of
of 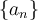 such that
such that 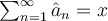 .
.
Answer:
True False
Question
56
Let 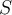 be the open unit disk
be the open unit disk 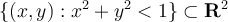 . Suppose that
. Suppose that 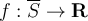 is continuous on
is continuous on 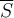 and differentiable on
and differentiable on 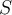 .
.
True or False: If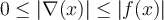 on S and
on S and 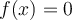 for some
for some 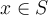 , then
, then 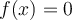 for all
for all 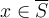 .
.
True or False: If
Answer:
True False
Question
57
Let 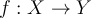 be a function with domain
be a function with domain 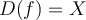 and range
and range 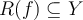 . True or False: For any
. True or False: For any 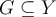 ,
, 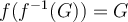 .
.
Answer:
True False
Question
58
Given a normed linear space 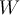 and
and 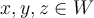 , is the following statement true or false:
, is the following statement true or false: 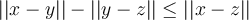 ?
?
Answer:
True False
Question
59
True or False: The countable union of open sets is open.
Answer:
True False
Question
60
Let 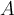 ,
, 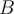 , and
, and 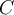 be sets. True or False:
be sets. True or False: 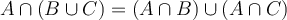 .
.
Answer:
True False