1
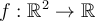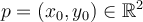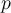Let and fix . Each of the derivatives stated in the below answer options is computed at . Given these conditions, which of the statements below is incorrect?
Choose one answer.
a. If the partial derivatives and are equal to , then is continuous at .
b. The directional derivative, if it exists, is a finite real number.
c. For all vectors and , with and , it holds that exists if, and only if, exists.
d. If the restriction of to the -axis has a minimum at , then .
.
.
Question 2
Let 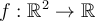be a function for which all directional derivatives at all points exist. Define a new function 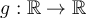by the formula 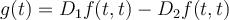. Given these conditions, which of the statements below is correct?
Choose one answer.
a. Regardless of what is, the function is never a constant.
b. If , then is constantly .
c. The function is infinitely differentiable.
d. If , then .
.
.
Question 3
Which of the statements below is incorrect?
Choose one answer.
a. The Jacobian of a function at a point can be a negative number.
b. Any positive number can arise as the Jacobian at the origin of some function .
c. If is invertible and differentiable at the origin, then the differential mapping at the origin is represented by a unique matrix.
d. If is continuous and satisfies for all , then is a linear transformation.
.
.
Question 4
Consider a function 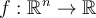and a point 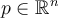. Which of the statements below is correct?
Choose one answer.
a. is differentiable at if, and only if, all partial derivatives of at exist.
b. is differentiable at if, and only if, is continuous in a neighborhood of .
c. is differentiable at if, and only if, is differentiable at .
d. is differentiable at if, and only if, there exists a linear transformation such that is differentiable at .
.
.
Question 5
Let 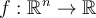be a function satisfying the homogeneity condition 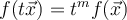for some 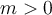. Which of the statements below is correct?
Choose one answer.
a. If is differentiable at , then .
b. is always differentiable at any point.
c. need not be continuous at the origin.
d. If the homogeneity condition is satisfied, then must actually be an integer.
.
.
Question 6
Consider the function 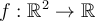, given by 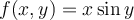. Which of the statements below is incorrect?
Choose one answer.
a. .
b. .
c. .
d. .
.
.
Question 7
For the functions 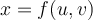and 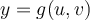, which answer option below results in a Jacobian that is not independent of ?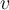
Choose one answer.
a. , .
b. , .
c. , .
d. , .
.
.
Question 8
Let 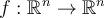be a function that is continuously differentiable at all points 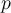. Which of the statements below is correct?
Choose one answer.
a. If at every point the Jacobian of is non-zero, then the function is globally invertible.
b. If at some point the Jacobian of is , then is not locally invertible at .
c. If the Jacobian of is at infinitely many points, then can be locally invertible at most finitely many points.
d. If the Jacobian of at every point is non-zero, then at every point the function is locally invertible.
.
.
Question 9
For each positive real number 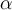, let 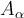be a subset of 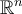. Which of the statements below is incorrect?
Choose one answer.
a. If each is meager, then the union is meager too.
b. If for all the set is meager, then the union is meager too.
c. If and is meager, then is meager too.
d. If and is not meager, then is not meager either.
.
.
Question 10
Let 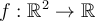be a function of class 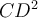. Write 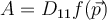, , 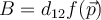and 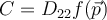. Given these conditions, which of the statements below is correct?
Choose one answer.
a. If has a maximum at , then .
b. If and , then can have a maximum at .
c. If , , and , then does not have a global minimum or maximum.
d. If does not have an extremum at and , then .
.
.
Question 11
Let 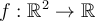be given and 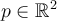a point. Further, let 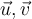be vectors in 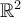. All the derivatives in the below answer options are computed at 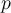. Without further knowledge about 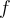other than that given in each statement below, which of the answer options below is correct?
Choose one answer.
a. If are independent and is continuous at , then any directional derivative can be determined from and .
b. If is differentiable at , then any directional derivative can be determined from and .
c. If is differentiable at , then any directional derivative can be determined from and if, and only if, the vectors are independent.
d. Since there are infinitely many directions in which to compute directional derivatives, knowledge of any finite number of directional derivatives is never sufficient to determine all directional derivatives.
.
.
Question 12
Let 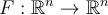be a function whose component functions 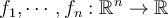all have continuous partial derivatives. Which of the statements below is correct?
Choose one answer.
a. If is locally invertible at every point in its domain, then the Jacobian is never .
b. If is not locally invertible at some point in its domain, then the Jacobian at that point is .
c. The Jacobian is either always positive or always negative.
d. If the Jacobian of attains a positive value and a negative value, then it also attains the value .
.
.
Question 13
Which of the statements below is incorrect?
Choose one answer.
a. For every , the set in is not meager.
b. The set is meager.
c. If is meager, then the set obtained from by adding to it all accumulation points of is also meager.
d. A closed set is never meager.
.
.
Question 14
The method of Lagrange multipliers typically is used to:
Choose one answer.
a. compute partial derivatives of a function conditioned on excluding particular directions.
b. find the largest value of where , conditioned on .
c. find the inverse of a function when the Inverse Function Theorem applies but does not yield an unconditioned value.
d. normalize the Jacobian, conditioned on the sign of the first partial derivatives.
.
.
Question 15
Let 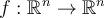be given. Which of the statements below is incorrect?
Choose one answer.
a. If is a linear transformation, then it is differentiable at all points.
b. If is differentiable at a point, then its behavior in a small-enough neighborhood of that point is approximated by a linear transformation.
c. If is differentiable and the Jacobian of is very large, then it is possible that the can be approximated at a point by two different linear transformations.
d. The Jacobian of cannot ever reveal information about how the volume of sets changes when is applied.
.
.
Question 16
Let 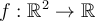be given. Which of the statements below is incorrect?
Choose one answer.
a. If is differentiable at the origin, then the restriction of to any straight line through the origin is continuous at the origin.
b. If is differentiable at the origin, then the restriction of to any straight line through the origin is differentiable at the origin.
c. If any restriction of to a line through the origin yields a continuous function, then it is still possible that is not differentiable at the origin.
d. is differentiable at the origin if, and only if, the restriction of along any straight line through the origin yields a function which is differentiable at the origin.
.
.
Question 17
Let 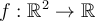be given such that 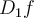, , 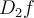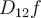and 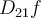all exist at every point 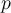in the domain. Fix a point 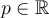. Which of the below statements relating to the differentiability at this point is correct?
Choose one answer.
a. , provided that or is continuous at .
b. if, and only if, and are continuous at .
c. implies that is differentiable at .
d. implies that is continuous at .
.
.
Question 18
Consider the function 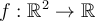given by the formula 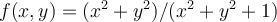. Which of the statements below is incorrect?
Choose one answer.
a. is continuous at the origin.
b. .
c. is differentiable at the origin.
d. has a minimum at the origin.
.
.
Question 19
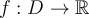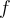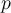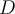Let be defined on some subset . Assume that is differentiable at a given point in . Which of the statements below is incorrect?
Choose one answer.
a. If attains a local minimum at , then all directional derivatives of at are equal to .
b. If attains a global minimum at , then, computed at , the equality must hold.
c. If attains a local minimum at a point , subject to a constraint given by , then for all , it holds that computed at is .
d. If attains a local minimum at a point , subject to a constraint given by a function , then for all that satisfy for all , it holds that computed at is .
.
.
Question 20
Which of the statements below is incorrect?
Choose one answer.
a. If are locally invertible at the origin, then the composite function is locally invertible at the origin.
b. The theorem that a function is locally invertible at the origin, provided , is a special case of the Inverse Function Theorem.
c. For every , there exists a function that is not locally invertible at any point of its domain.
d. If and are such that is not locally invertible at the origin, then at least one of or cannot be locally invertible at the origin.
.
.
Question 21
Let 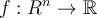be a function, and a rectangle. Which of the statements below is incorrect?
Choose one answer.
a. If , then exists.
b. If , then exists.
c. If exists, then .
d. If exists, then .
.
.
Question 22
Which of the statements below is incorrect?
Choose one answer.
a. The set of all rational numbers is a set of zero content.
b. The set of all irrational numbers is a set of zero content.
c. A countable union of sets of zero content is itself a set of zero content.
d. Any finite set is a set of zero content.
.
.
Question 23
be a function and a rectangle such that is Riemann integrable over . Which of the following statements about the number is correct?
Choose one answer.
a. If is satisfied for infinitely many values , then .
b. If is continuous on , then either or .
c. If the set is of zero content, then .
d. If is continuous on and satisfies for infinitely many points , then .
.
.
Question 24
Which of the following functions 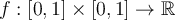is not Riemann integrable?
Choose one answer.
a. .
b. if , if , and otherwise .
c. , when and , and in all other cases, .
d. , when and , and in all other cases, .
.
.
Question 25
Let 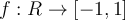, with 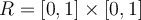. Which of the statements below is correct?
Choose one answer.
a. If is continuous in , then .
b. If is Riemann integrable on , then for all , the function is Riemann integrable on .
c. If for all , the function is Riemann integrable on , then is Riemann integrable on .
d. If , then for all , it holds that , provided the integral exists.
.
.
Question 26
Let 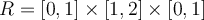and 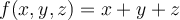. What can be said about ?
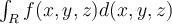Choose one answer.
a. The integral does not exist.
b. The integral exists and equals .
c. The integral exists and equals .
d. The integral exists, but its value can't be evaluated in closed form.
.
.
Question 27
Let 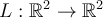be a linear transformation, and let 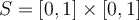. Which of the statements below is correct?
Choose one answer.
a. The Jordan content of is never equal to the Jordan content of .
b. If is invertible, then the Jordan content of is equal to the determinant of .
c. If is invertible, then the Jordan content of is equal to the absolute value of the determinant of .
d. The Jordan content of is equal to the absolute value of the determinant of .
.
.
Question 28
The answer options below are concerned with subsets of 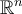. Which of the statements below is incorrect?
Choose one answer.
a. The union of finitely many Jordan measurable subsets is itself Jordan measurable.
b. The intersection of a Jordan measurable subset and a set of zero content is itself a set of zero content.
c. If and is not Jordan measurable, then is not Jordan measurable.
d. If and is Jordan measurable, then is Jordan measurable.
.
.
Question 29
Let 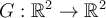and 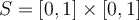. Assuming that the integrals below exist, under which of the conditions below is the formula 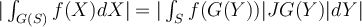guaranteed to hold?
Choose one answer.
a. If is a linear transformation such that is itself a square of area .
b. If for all .
c. The stated equality never holds.
d. The stated equality always holds.
.
.
Question 30
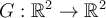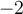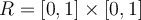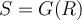Let be a linear transformation with determinant . Let , , and 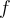be Riemann integrable on a rectangle containing 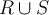. Which of the statements below is necessarily correct?
Choose one answer.
a. .
b. .
c. .
d. .
.
.
Question 31
Let 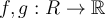, where 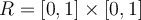, be Riemann integrable. Assume that for all 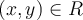, it holds that 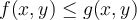. Which of the following statements is true?
Choose one answer.
a. If holds for infinitely many points, then .
b. If , then holds for all but finitely many points.
c. If , then holds for infinitely many points.
d. All of the answer options above hold true.
.
.
Question 32
Let 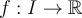, where 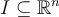is some non-degenerate rectangle (i.e., it has positive 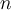-dimensional volume). Which of the following statements is correct?
Choose one answer.
a. If is not bounded, then is not Riemann integrable.
b. If satisfies that for all , and is of zero content, then is Riemann integrable if, and only if, is Riemann integrable.
c. If is continuous and positive at at least one point, then implies that attains negative values.
d. All of the answer options above are correct.
.
.
Question 33
Let 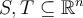. Which of the statements below is incorrect?
Choose one answer.
a. If is Jordan measurable, then so is .
b. If is Jordan measurable, then so is the closure .
c. If and are Jordan measurable, then so is .
d. If and are Jordan measurable and , then is Jordan measurable.
.
.
Question 34
Consider the region 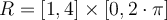. The polar coordinate transformation 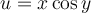, 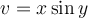achieves which of the following?
Choose one answer.
a. It transforms the region in the plane into an annulus in the plane, with the outer circle having radius .
b. It transforms the region in the plane into an annulus in the plane, with the outer circle having radius .
c. It transforms the region in the plane into an annulus in the plane, with the outer circle having radius .
d. It transforms the region in the plane into an annulus in the plane, with the outer circle having radius .
.
.
Question 35
Which of the following functions 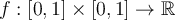is Riemann integrable?
Choose one answer.
a. if either or is rational, and otherwise.
b. , if both and , and otherwise.
c. if , and if .
d. All of the answer options above are Riemann integrable functions.
.
.
Question 36
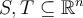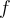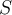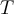Let be Jordan measurable, and be a function that is integrable on both and . Which of the statements below is correct?
Choose one answer.
a. If and , then .
b. If , then .
c. If , then the Jordan measure of and is the same.
d. If and , then .
.
.
Question 37
Which of the following subsets 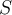of 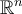, with 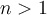, is of zero content?
Choose one answer.
a. , since .
b. , since it is a union of sets of zero content (recall that is the -dimensional sphere).
c. where , since is negligible.
d. All of the answer options above describe sets of zero content.
.
.
Question 38
Let 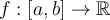and 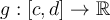be continuous functions. Let 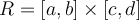. Assume that 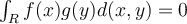. Which of the statements below is correct?
Choose one answer.
a. Both and .
b. Either or .
c. For all , either or .
d. For all , both and .
.
.
Question 39
Let 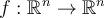. Which of the following statements is incorrect?
Choose one answer.
a. There exists an infinite subset such that is Riemann integrable on .
b. If is integrable on a rectangle , then is bounded on .
c. If is discontinuous, then there exists a rectangle such that is not Riemann integrable on .
d. If is constantly , then is integrable on any rectangle.
.
.
Question 40
Let 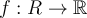where 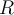is a non-trivial rectangle in 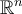. Which of the statements below is correct?
Choose one answer.
a. If is both continuous and integrable, then is a constant.
b. is continuous if, and only if, is integrable.
c. If is integrable, then is continuous.
d. If is continuous, then is integrable.
.
.
Question 41
Which of the following answer options is a 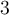-form on ?
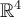Choose one answer.
a. .
b. .
c. .
d. .
.
.
Question 42
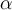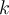Let be a -form on 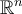. Which of the following statements is correct?
Choose one answer.
a. if, and only if, .
b. If is odd, then .
c. If is odd, then .
d. if, and only if, both and are odd.
.
.
Question 43
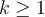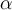Let and be a 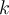-form on 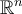. Which of the following statements is incorrect?
Choose one answer.
a. .
b. .
c. .
d. if, and only if, or .
.
.
Question 44
In 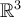, which of the following statements is correct?
Choose one answer.
a. .
b. .
c. for all forms on .
d. if, and only if, .
.
.
Question 45
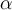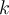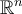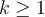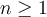Let be a -form on , with and . Which of the following statements is correct?
Choose one answer.
a. If is exact, then is closed.
b. If is closed, then is exact.
c. If is closed and exact, then .
d. The validity or invalidity of each answer option above depends on the values of and .
.
.
Question 46
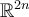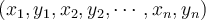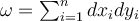Consider with coordinates . Let , and let 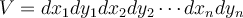denote the volume form on 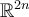. Which of the following statements is correct?
Choose one answer.
a. .
b. .
c. .
d. .
.
.
Question 47
Let 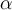be the form 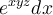. Which of the following answer options is equal to ?
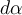Choose one answer.
a. .
b. .
c. .
d. .
.
.
Question 48
Let 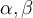be 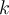-forms on 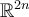. Which of the following statements is correct?
Choose one answer.
a. .
b. .
c. If , then .
d. If , then .
.
.
Question 49
Let 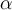and 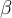be differential forms on 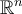. Which of the following statements is incorrect?
Choose one answer.
a. If and are closed, then is exact.
b. If and are exact, then is closed.
c. If and are exact, then is exact.
d. If and are closed, then is closed.
.
.
Question 50
Let 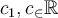be constants. Consider the form 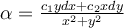. For which of the following answer options is 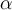closed?
Choose one answer.
a. .
b. .
c. .
d. All of the answer options above lead to a closed form.
.
.
Question 51
Let 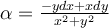and 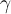be the unit circle curve, parametrized counterclockwise. What is the value of ?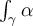
Choose one answer.
a.
b.
c.
d.
.
.
Question 52
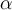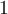Let be a -form on 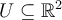and let 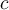be a curve for which 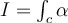exists. Which of the following statements is correct?
Choose one answer.
a. If , then is exact.
b. If and is closed, then is exact.
c. If is closed and is closed, then .
d. If is exact and is closed, then .
.
.
Question 53
Consider a closed curve 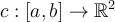satisfying 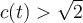for all 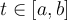, and let 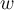be the winding number of 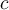. Which of the following statements is correct?
Choose one answer.
a. .
b. , provided is parametrized counterclockwise, and if is parametrized clockwise.
c. .
d. .
.
.
Question 54
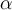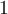Let be a -form on 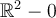and let 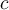be a curve that does not pass through the origin. Which of the following statements is correct?
Choose one answer.
a. If is the global angle form, then .
b. If is the global angle form and is closed, then is an integral multiple of .
c. If is closed and is an integer, then is the global angle form.
d. All of the above answer options are correct.
.
.
Question 55
Which of the following statements regarding chains, boundaries, cycles, and forms is correct?
Choose one answer.
a. If is a -form and a degenerate -chain, then .
b. The boundary of a degenerate -chain is a degenerate -chain.
c. Every boundary is a cycle.
d. All of the above statements are correct.
.
.
Question 56
Which of the following statements regarding chains and boundaries is correct?
Choose one answer.
a. Every cycle is a boundary.
b. holds for at least one chain .
c. A chain is a boundary if, and only if, it is a cycle.
d. All of the statements above are incorrect.
.
.
Question 57
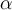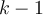Let be a -form on an open set and let 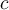be a 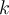-chain. Which of the following equalities is guaranteed to hold?
Choose one answer.
a. .
b. .
c. .
d. None of the above equalities is correct.
.
.
Question 58
When the most general Stokes' Theorem is applied to the 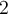-form 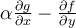to compute the integral 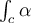, where 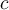is a smooth curve in 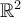enclosing a region in which 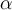is defined, what is the resulting formula's name?
Choose one answer.
a. Stokes' Formula.
b. Green's Formula.
c. Gauss' Formula.
d. The resulting formula has no particular name.
.
.
Question 59
The determinant of an 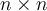matrix whose columns form a linearly dependent set is known to be 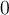. Which of the following statements is a correct geometric explanation for this fact?
Choose one answer.
a. Such a matrix represents a linear transformation whose values are independent of a particular choice of coordinates. Since volume depends on coordinates, the determinant must be .
b. Such a matrix represents a linear transformation whose values are dependent on a particular choice of basis. Since volume depends on the basis, the determinant must be .
c. The columns of the matrix, being dependent, determine a degenerate region in which thus has -dimensional volume equal to .
d. All of the above statements are correct geometric explanations.
.
.
Question 60
The pullback operator connects which of the following two concepts?
Choose one answer.
a. The global angle form and the gradient.
b. The global angle form and the Jacobian.
c. The volume forms and the gradient.
d. The volume forms and the Jacobian.
.
.