1
Let 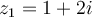 , and let
, and let 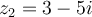 . What is
. What is 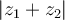 ?
?
Answer:
Question
2
Let 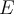 denote the punctured unit disk:
denote the punctured unit disk: 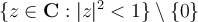 . Which of the following is false?
. Which of the following is false?
Choose one answer.
|
A. 0 is an isolated point of |
||
|
B. 0 is a boundary point of |
||
|
C. 0 is an accumulation point of |
||
|
D. |
||
|
E. |
Question
3
Consider the set 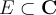 given by
given by 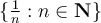 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
4
Given two complex numbers 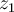 and
and 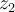 with principle arguments
with principle arguments 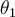 and
and 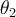 and magnitudes
and magnitudes 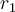 and
and 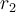 , respectively, which of the following is false?
, respectively, which of the following is false?
Choose one answer.
|
A. The magnitude of |
||
|
B. The principle argument of |
||
|
C. The magnitude of |
||
|
D. If |
||
|
E. If |
Question
5
If 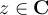 satisfies
satisfies 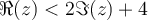 , writing
, writing 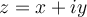 , which of the following statements holds?
, which of the following statements holds?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of these choices |
Question
6
Let 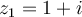 , and let
, and let 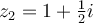 . What is the principle argument (i.e. the argument in
. What is the principle argument (i.e. the argument in 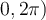 ) of
) of  ?
?
Answer:
Question
7
Let 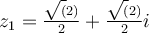 , and let
, and let 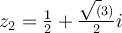 . What is the principle argument (i.e. in
. What is the principle argument (i.e. in 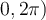 ) of
) of 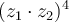 ?
?
Answer:
Question
8
Suppose that 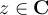 with
with 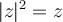 . What is the modulus of
. What is the modulus of 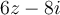 ?
?
Answer:
Question
9
Which of the following pairs of functions fails to satisfy the Cauchy-Riemann equations?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
10
Let 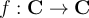 , with
, with 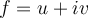 , where
, where 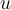 and
and 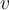 are real-valued. Let
are real-valued. Let 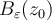 denote the ball of radius
denote the ball of radius 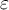 centered at
centered at 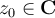 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. In order for |
||
|
B. In order for |
||
|
C. In order for |
||
|
D. In order for |
||
|
E. In order for |
Question
11
Which of the following is true of the complex-valued function 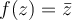 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of these choices |
Question
12
Let 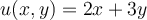 be the real part of an analytic function.
Which of the following is the harmonic conjugate,
be the real part of an analytic function.
Which of the following is the harmonic conjugate, 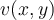 ,
of
,
of 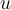 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. None of these choices |
Question
13
Let 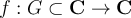 . Let
. Let 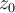 be an accumulation point of
be an accumulation point of 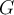 , and let
, and let 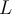 be a complex number. Choose the correct definition for the following
statement:
be a complex number. Choose the correct definition for the following
statement: 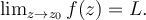
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
14
Which of the following statements about the complex exponential function 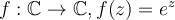 is false?
is false?
Choose one answer.
| A. The complex exponential is periodic. | ||
| B. The complex exponential is onto (i.e. surjective). | ||
|
C. The complex exponential satisfies |
||
| D. The complex exponential is holomorphic. | ||
|
E. The complex exponential satisfies |
Question
15
Let 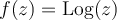 be the principle value of the logarithm. Which
of the following could be the preimage of the set
be the principle value of the logarithm. Which
of the following could be the preimage of the set 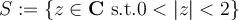 ?
?
Choose one answer.
|
A. The annulus |
||
|
B. The annulus |
||
|
C. The punctured disc |
||
|
D. The punctured disc |
||
| E. None of these choices |
Question
16
Let 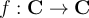 be given by
be given by 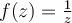 . Let
. Let 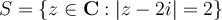 . Then which of the following is true?
. Then which of the following is true?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
17
Let 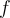 be the Moebius transformation such that
be the Moebius transformation such that
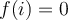 ,
, 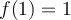 , and
, and 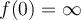 . What is
. What is 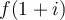 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
18
What is the modulus of the principle value of 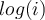 ?
(Give two decimal places of precision.)
?
(Give two decimal places of precision.)
Answer:
Question
19
True or false: A well-defined principle branch of the complex logarithm is an entire function.
Answer:
True False
Question
20
True or false: There exists a Moebius transformation which has derivative equal to zero at the origin.
Answer:
True False
Question
21
Suppose 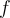 is a function on an open set
is a function on an open set
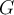 . Let
. Let 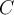 be a piecewise smooth, simple curve in
be a piecewise smooth, simple curve in 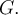 Let
Let 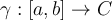 be a smooth parametrization of
be a smooth parametrization of 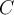 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. If |
||
|
B. If |
||
|
C. If |
||
|
D. If |
||
| E. None of these choices |
Question
22
Define the following contours: 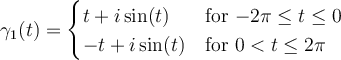
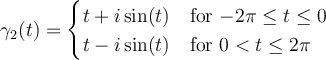
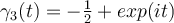 for
for 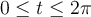 .
.
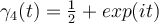 for
for 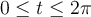 .
.
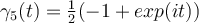 for
for 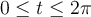 .
.
Which of the following is true?
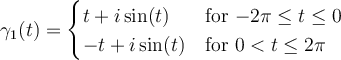
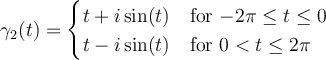
Which of the following is true?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. The winding number of |
Question
23
Let 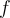 be a function which is analytic on a domain
be a function which is analytic on a domain
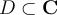 , and let
, and let 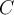 be a simple contour in
be a simple contour in 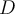 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. In order to have |
||
|
B. In order to have |
||
|
C. In order to have |
||
|
D. In order to have |
||
|
E. In order to have |
Question
24
Which of the following smooth curves in the complex plane is longest?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
25
Which of the following is true?
Choose one answer.
| A. Analytic functions which are bounded on a subset of their domain are constant on that subset. | ||
|
B. |
||
|
C. If |
||
|
D. If |
||
|
E. If a function |
Question
26
Let 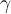 be the positively oriented circle of radius
be the positively oriented circle of radius
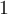 centered at
centered at 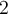 in the complex plane. What is the value of
in the complex plane. What is the value of 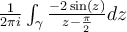 ?
?
Answer:
Question
27
Let 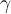 be the positively oriented circle of radius
be the positively oriented circle of radius
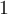 centered at
centered at 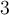 in the complex plane. What is the value of
in the complex plane. What is the value of 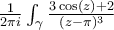 ?
?
Answer:
Question
28
Compute 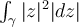 , where
, where 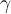 is the line segment from
is the line segment from 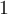 to
to 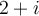 . (Give precision to the hundredths place.)
. (Give precision to the hundredths place.)
Answer:
Question
29
Let 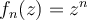 . Let
. Let 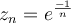 . Let
. Let 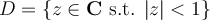 . Which of the following is false?
. Which of the following is false?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
30
Consider the power series 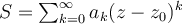 . Which of the following
is false?
. Which of the following
is false?
Choose one answer.
|
A. The radius of convergence is at least 1 if |
||
|
B. The radius of convergence is at most 1 if |
||
|
C. If |
||
|
D. If there exists |
||
|
E. If |
Question
31
What is the radius of convergence for the following power series in 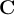 :
: 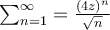 ?
?
Answer:
Question
32
Suppose a sequence of continuous functions 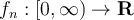 converges uniformly to zero on
converges uniformly to zero on 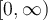 . True or false:
. True or false:
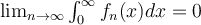 .
.
Answer:
True False
Question
33
Suppose a function 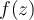 has a Laurent series of the form
has a Laurent series of the form
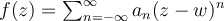 . Match the type of function with its Laurent
series.
. Match the type of function with its Laurent
series.
|
|
||
|
A nonzero, finite number of the coefficients |
||
|
An infinite number of the coefficients |
Question
34
Consider the function 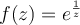 . Denote the punctured unit
disc by
. Denote the punctured unit
disc by 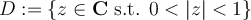 . Let
. Let 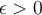 and
and 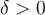 . Which of the following statements is false?
. Which of the following statements is false?
Choose one answer.
|
A. Given any point |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
35
Consider the function 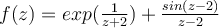 on
on 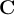 . Which of the following is true about the singularities of
. Which of the following is true about the singularities of  ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
36
Consider the function 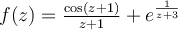 . Which of the following
statements is true?
. Which of the following
statements is true?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
37
The proof that holomorphic functions on open, connected sets have power series representations relies on which of the following results?
Choose one answer.
| A. Morera's theorem | ||
| B. Cauchy's integral formula | ||
| C. Poisson's integral representation | ||
| D. Liouville's theorem | ||
| E. Riemann mapping theorem |
Question
38
Let 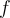 and
and 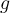 be non-constant holomorphic functions on
be non-constant holomorphic functions on 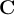 with
with 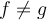 . Let
. Let 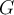 be a bounded domain. Which of the following is possible?
be a bounded domain. Which of the following is possible?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. There exists a contour |
Question
39
Let 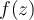 be a meromorphic function defined on
be a meromorphic function defined on
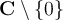 by
by 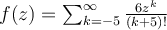 . Let
. Let 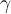 be parameterized by
be parameterized by 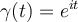 ,
, 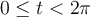 . What is the value of
. What is the value of 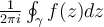 ?
?
Answer:
Question
40
Calculate the residue of 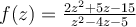 at
at 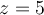 .
.
Answer:
Question
41
Calculate the residue of 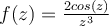 at
at 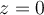 .
.
Answer:
Question
42
Let 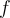 be a function on an open set
be a function on an open set 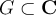 with singularities at
with singularities at  . Let
. Let 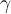 be a closed curve in
be a closed curve in 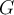 . Which of the conditions below is not necessary for the following
formula to hold?
. Which of the conditions below is not necessary for the following
formula to hold? 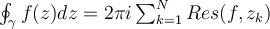
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. The singularities |
||
| E. All of these choices are necessary. |
Question
43
Suppose 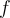 is a function that is holomorphic inside
and on a simple, closed curve
is a function that is holomorphic inside
and on a simple, closed curve 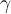 , and that for all
, and that for all
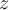 inside and on
inside and on 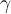 ,
, 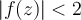 . Which of the following is false?
. Which of the following is false?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
44
Let 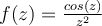 . Let
. Let 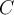 be the positively oriented circle of radius 2, centered at the origin.
What is the value of
be the positively oriented circle of radius 2, centered at the origin.
What is the value of 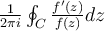 ?
?
Answer:
Question
45
Let 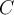 be the positively oriented circle of radius 2,
centered at the origin. What is the value of
be the positively oriented circle of radius 2,
centered at the origin. What is the value of 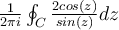 ?
?
Answer:
Question
46
Let 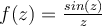 . Let
. Let 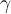 be parameterized by
be parameterized by 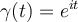 ,
, 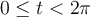 . What is the value of
. What is the value of 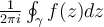 ?
?
Answer:
Question
47
Compute 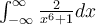 . (Hint: use residues.) Your answer should
be correct to the hundredths place.
. (Hint: use residues.) Your answer should
be correct to the hundredths place.
Answer:
Question
48
Compute 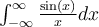 . (Hint: use a half-annulus contour.) Your
answer should be correct to the hundredths place.
. (Hint: use a half-annulus contour.) Your
answer should be correct to the hundredths place.
Answer:
Question
49
Let 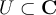 be an open set. Let
be an open set. Let 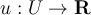 . Which of the following is true?
. Which of the following is true?
Choose one answer.
|
A. In order for |
||
|
B. In order for |
||
|
C. In order for |
||
|
D. In order for |
||
|
E. In order for |
Question
50
Let 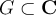 be a simply connected, open set. Let
be a simply connected, open set. Let
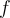 be an entire function, and let
be an entire function, and let 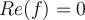 on
on 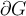 . Which of the following is the strongest statement that can be made
about
. Which of the following is the strongest statement that can be made
about 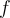 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
51
True or false: Consider a function 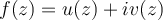 , where
, where
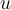 and
and 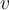 are real-valued. Let
are real-valued. Let 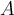 be the annulus
be the annulus 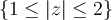 , and let
, and let 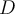 be the disc
be the disc  . Suppose that
. Suppose that 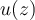 achieves its maximum in
achieves its maximum in 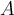 on the interior of
on the interior of 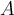 . Then
. Then 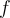 cannot be holomorphic in
cannot be holomorphic in 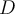 .
.
Answer:
True False
Question
52
Let 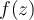 be a map which is conformal from
be a map which is conformal from 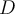 to
to 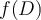 , where
, where 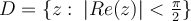 . Which of the following is a possible choice for
. Which of the following is a possible choice for 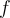 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
53
Let 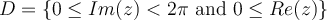 . If
. If 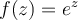 , what is
, what is 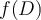 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
54
Let 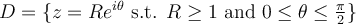 . Define a mapping on
. Define a mapping on 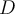 by
by 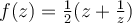 . What is
. What is 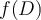 ?
?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
|
E. |
Question
55
Suppose that 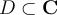 is a simply connected, open set. Let
is a simply connected, open set. Let
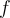 be a nonconstant function. Which of the following
is true?
be a nonconstant function. Which of the following
is true?
Choose one answer.
|
A. In order for |
||
|
B. In order for |
||
|
C. In order for |
||
|
D. In order for |
||
|
E. In order for |
Question
56
Let 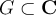 , and let
, and let 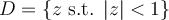 . If an analytic bijection does not exist between
. If an analytic bijection does not exist between 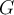 and
and 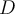 , which of the following is not a possible cause?
, which of the following is not a possible cause?
Choose one answer.
|
A. |
||
|
B. |
||
|
C. |
||
|
D. |
||
| E. Both A and B |