Brennen was adding using a number line. He started on 12 and ended on -3. What number did he add to 12?

Choose one answer.

	a. 9
	b. -9
	c. 15
	d. -15

Question 2

Caleb was scuba diving. He descended, or went deeper into the water, 12.5 meters at a time, and then he would stop to check out his surroundings. After descending five times, what rational number could be used to describe his location?

Choose one answer.

	a. 17.5 meters
	b. -17.5 meters
	c. 62.5 meters
	d. -62.5 meters

Question 3

Gregg owns a small store. After he purchases materials to sell, he marks up the prices by 15%. If he is selling an item for $20.60, what did he pay for the item originally?

Choose one answer.

	a. $17.91
	b. $17.51
	c. $20.45
	d. $23.69

Question 4

Hannah started with $548.92 in her checking account. In the check register she wrote -$34.88 and -12.71 to show the amounts of money she spent at two stores. What is her new account balance?

Choose one answer.

	a. $526.75
	b. $571.09
	c. $501.33
	d. $596.51

Question 5

Jerod completed 32% of the yard work while Marty completed 14% of the yard work. Which decimal represents the amount of work they completed together?

Choose one answer.

	a. 0.18
	b. 0.46
	c. 0.046
	d. 0.018

Question 6

Marissa and Cami went on vacation. Marissa went to Alaska, where the temperature was -3 ⁰F. Cami is in Texas where it is 95 ⁰F. How much warmer is it in Texas than Alaska?

Choose one answer.

	a. 92⁰
	b. -92⁰
	c. 98⁰
	d. -98⁰

Question 7

Molly purchased a hat that was 20% off. She paid $24. Which of the following amounts shows the original price?

Choose one answer.

	a. $30
	b. $28.80
	c. $28
	d. $21.20

Question 8

Patty placed $4,500 in a savings account for 10 years earning a rate of 2.8%. How much interest did she earn?

Choose one answer.

	a. $12.60
	b. $126
	c. $1,260
	d. $12,600

Question 9

Solve the following expression: 12.4 ÷ 4 + 3.2 - 9.71 x 2.

Choose one answer.

	a. -6.82
	b. -12.12
	c. -13.12
	d. 19.32

Question 10

The numerical expression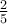

+ (-

) -

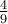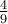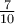is equal to:

Choose one answer.

	a. -
	b.
	c. -
	d.

Question 11

The water level changes by -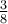

of an inch every two years in Carlos's pond. How much will the water level have changed after six years?

Choose one answer.

	a. -
	b. -
	c. -
	d. -

Question 12

Tyron purchased a coat on sale 30% off. The original price was $150. After the discount is taken off and 4% tax is added on, what is the final cost?

Choose one answer.

	a. $111.00
	b. $109.20
	c. $99.00
	d. $46.80

Question 13

Which of the following choices shows the amounts in order from least to greatest?

Choose one answer.

	a. 45%, 0.5,
	b. 80%, , 0.492
	c. , 65%, 0.329
	d. , 0.31, 49%

Question 14

Which of the following is the final price of an item bought for $26 with a 6% sales tax added on?

Choose one answer.

	a. $24.44
	b. $26.06
	c. $26.60
	d. $27.56

Question 15

Which of the following shows the decimal and fraction version of 12.5%?

Choose one answer.

	a. 0.125,
	b. 12.5,
	c. 0.125,
	d. 12.5,

Question 16

Yvonne works as a real estate agent. She earns a 3% commission on each house she sells. Last week she sold a home for $130,000. Which of the following expressions could be used to calculate how much Yvonne earned?

Choose one answer.

	a. $130,000(0.3)
	b. $130,000(0.03)
	c. $130,000 ÷ 0.3
	d. $130,000 ÷ 0.03

Question 17

A painter was paid $500 for 40 hours of work painting houses. What is the unit rate and what does it mean?

Choose one answer.

	a. $12.50 per hour, which is the amount that the painter was paid each hour
	b. 12.50 hours, which is the amount of time spent on the job each day
	c. $8 per hour, which is the amount that the painter was paid each hour
	d. 8 hours, which is the amount of time spent on the job each day

Question 18

For every eight minutes that Patty runs, she completes another mile. Which of the following equations shows this proportional relationship, where x is the minutes and y is the number of miles?

Choose one answer.

	a. y = 8x
	b. y = x
	c. y = x + 8
	d. y = x - 8

Question 19

For every three dishes Kyla cleans, Makenzie cleans five. Which of the following proportions can be used to determine how many dishes Makenzie cleans if Kyla cleans 38?

Choose one answer.

	a. =
	b. =
	c. =
	d. =

Question 20

Frank is planning out a design for a home. The design includes a bedroom with a rectangular floor. The length of the actual bedroom will be 15 feet. On the blueprint, the length is 3 inches. He notices that the area of the bedroom on the blueprint is 6 in

. What is the actual width of the bedroom?

Choose one answer.

	a. 5 feet
	b. 10 feet
	c. 20 feet
	d. 30 feet

Question 21

Given the following four shapes, which two are similar?

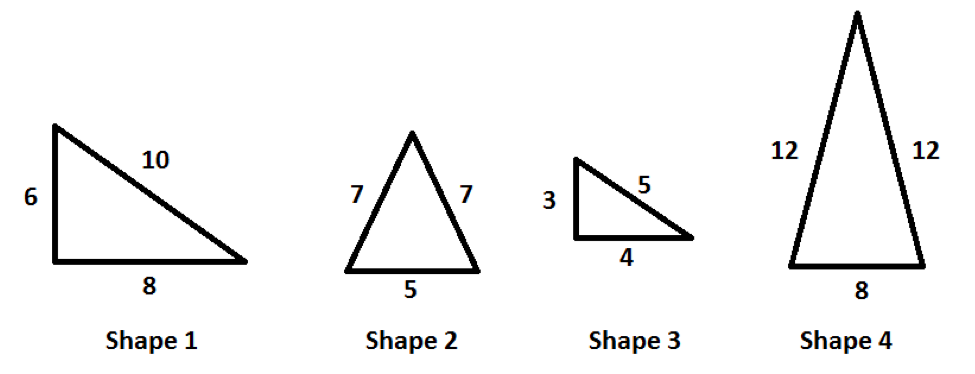
Choose one answer.

	a. Shape 1 and Shape 2
	b. Shape 2 and Shape 4
	c. Shape 2 and Shape 3
	d. Shape 1 and Shape 3

Question 22

Gurnaz is solving the proportion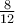

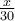. Which of the following sets of cross products could be used to solve for x?

Choose one answer.

	a. 15x = 4*6
	b. 30x = 8*12
	c. 2x = 3*30
	d. 12x = 8*30

Question 23

Henry can mow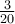

of his lawn in 15 minutes. At this rate, how much of his lawn can he mow in one hour?

Choose one answer.

	a.
	b.
	c.
	d.

Question 24

In the proportion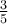

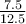, the original ratio has been scaled up by a factor of:

Choose one answer.

	a. 2.5.
	b. 4.5.
	c. 7.5.
	d. 37.5.

Question 25

Mark is painting the examination rooms in a medical building. The relationship between the blue and the white paint used in each room is proportional. If he uses two parts blue for every six parts white, which of the following equations compares the amount of white paint, w , to the amount of blue paint, b?

Choose one answer.

	a. w = b
	b. b = 3w
	c. b = w
	d. b = w

Question 26

On a map, two cities are 5 inches apart. If the scale used to create the map is 2 inches : 30 miles, what is the actual distance between the two cities?

Choose one answer.

	a. 150 miles
	b. 120 miles
	c. 75 miles
	d. 65 miles

Question 27

The following two shapes are similar. What is the scale factor that can be used to determine the length of x?

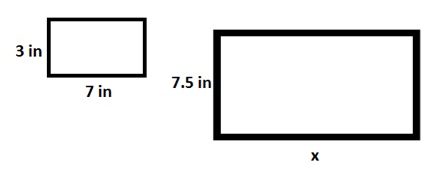
Choose one answer.

	a. 0.5
	b. 2.5
	c. 3.5
	d. 4

Question 28

There are two girls for every three boys at the concert. Which of the following ratios compares the boys to the total in three different ways?

Choose one answer.

	a. 3 : 2, 3 to 2,
	b. 2 to 5, , 2 x 5
	c. 3 : 5, 3 to 5,
	d. 2 to 3, 2 x 3,

Question 29

Which of the following equations describes the proportional relationship shown in the graph?

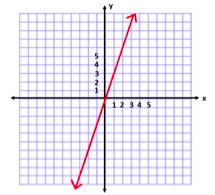
Choose one answer.

	a. y = 3x
	b. y = x
	c. x = 3y
	d. x = y + 3

Question 30

Which of the following ratios is equivalent to 30 : 45?

Choose one answer.

	a.
	b. 10 to 15
	c. 9 : 6
	d. 90 to 60

Question 31

Which of the following shows an example of a proportion?

Choose one answer.

	a. =
	b. =
	c. =
	d. =

Question 32

Which of the following shows the better buy?

Choose one answer.

	a. Five apples for $3.00
	b. Four apples for $2.60
	c. Ten apples for $6.60
	d. Twenty apples for $12.40

Question 33

Caleb wants to purchase a pair of shoes and some T-shirts. He wants to spend less than $100. The pair of shoes costs $38 and each T-shirt costs $10. Which of the following inequalities could be used to determine how many T-shirts Caleb can buy?

Choose one answer.

	a. 10x + 38 > 100
	b. 10x + 38 < 100
	c. 38x + 10 > 100
	d. 38x + 10 < 100

Question 34

DeShawn is growing a plant for a science project. The plant was x cm tall yesterday and it grows 11% each day. Which of the following expressions could represent the height of the plant today?

Choose one answer.

	a. x + 0.11x
	b. 0.11x
	c. x * 0.11x
	d. x + 0.11

Question 35

Franca wants to buy a pair of shoes. There will be an additional 4% added on for tax. Which expression could be used to determine the final cost of the shoes?

Choose one answer.

	a. x + 0.04
	b. 0.04x
	c. x + 0.04x
	d. x - 0.04x

Question 36

In which of the following equations does x = -5?

Choose one answer.

	a. 2x + 9 = -19
	b. 3x - 7 = -22
	c. -2x - 3 = -13
	d. -4x + 2 = 18

Question 37

Maria can spend, at most, $40 at the fair. It costs $5 to get in and then $0.25 per ticket. Which of the following inequalities shows how many tickets she can buy?

Choose one answer.

	a. $0.25 + $5 $40
	b. $0.25x + $5 $40
	c. $5x + $0.25 $40
	d. ($5 + $0.25) x $40

Question 38

Renita hired a plumber. In the estimate, she was told that the supplies for the job would cost $120 and that there would be a $40 per hour charge for the labor. If she only has $280 to spend on the job, which of the following equations can be used to determine how many hours (x) she can afford?

Choose one answer.

	a. 40x + 120 = 320
	b. 120x + 40 = 320
	c. (120 - 40)x = 320
	d. (120 + 40)x = 320

Question 39

Simplify the following expression: 5(3x - 9) + 11x + 4.

Choose one answer.

	a. 26x - 5
	b. 19x - 5
	c. 26x - 41
	d. 19x - 41

Question 40

Solve the following inequality: 7x + 2x - 1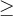8

-108.

Choose one answer.

	a. x 14
	b. x -14
	c. x -10
	d. x -10

Question 41

The first step in solving -8x + 3 = -21 would be to:

Choose one answer.

	a. add 3 to both sides of the equation.
	b. subtract 3 from both sides of the equation.
	c. divide both sides of the equation by -8.
	d. add 8 to both sides of the equation.

Question 42

What is the value of x in the following equation: 3(2x + 5) = -18 + 5?

Choose one answer.

	a. -24
	b. -12
	c. 3
	d. -3

Question 43

Which number line shows the solution to the following inequality: 6y + 3y - 11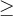

70?

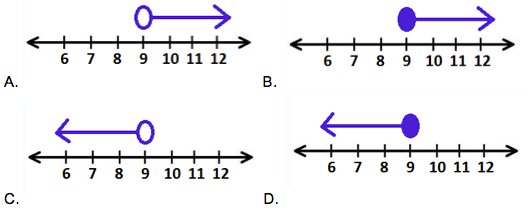
Choose one answer.

	a. A
	b. B
	c. C
	d. D

Question 44

Which of the following expressions could be written as 4 - 3x?

Choose one answer.

	a. 4 less than the product of 3 and x
	b. 4 minus the quotient of 3 and x
	c. 4 reduced by the difference of 3 and x
	d. 4 diminished by the product of 3 and x

Question 45

Which of the following expressions is equivalent to 7(x + y)?

Choose one answer.

	a. 7(xy)
	b. (7 + x)(7 + y)
	c. 7+ xy
	d. 7x + 7y

Question 46

Which of the following expressions represents the sum of (2x + 5y) and (-7x + 3y)?

Choose one answer.

	a. 3xy
	b. 5x + 8y
	c. -5x + 8y
	d. -5x² + 8y²

Question 47

Which of the following expressions will be equal to 13 when x = 4 and y = -2?

Choose one answer.

	a. 5x + 3y - 9
	b. 5x + 4y + 1
	c. 6x - 5y - 1
	d. 3x - 2y + 5

Question 48

Which value of y will make the following statement true: y(2x + 3) + 5 = -8x - 7?

Choose one answer.

	a. -4
	b. 4
	c. -6
	d. 6

Question 49

A dog is tied to a post in the middle of a large backyard. If the rope used to tie the dog is 30 feet long, what is the area of the space the dog can roam? The answer should be in terms of pi.

Choose one answer.

	a. 30π ft²
	b. 225π ft²
	c. 900π ft²
	d. 3,000π ft²

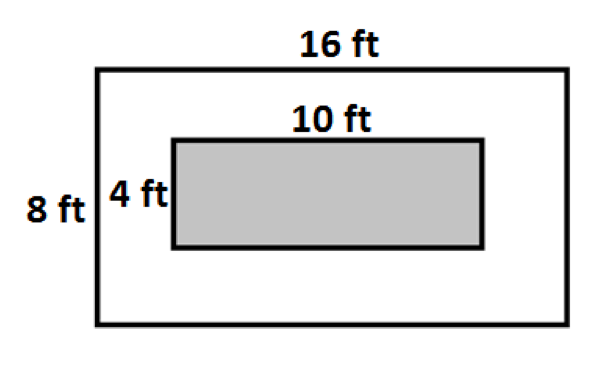
Question 50

A hole was drilled into a piece of wood, as shown below. What is the area of the remaining wood?

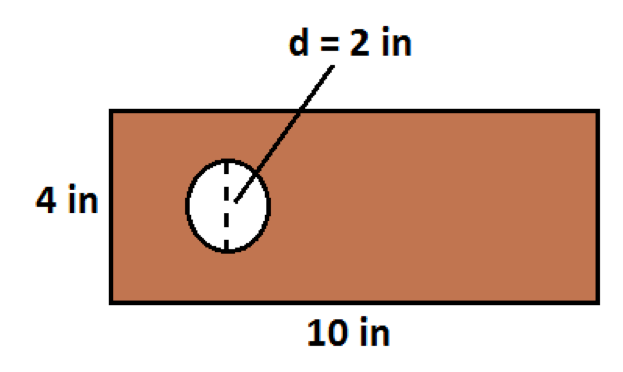
Choose one answer.

	a. 38 in²
	b. 27.44 in²
	c. 33.14 in²
	d. 36.86 in²

Question 51

A rectangle has an area of 160 ft² and a base of 16 ft. What is the height of the rectangle?

Choose one answer.

	a. 40 feet
	b. 16 feet
	c. 10 feet
	d. 8 feet

Question 52

Bella wants to create a package that has one-fourth the surface area of the original package. How would she change the lengths of the sides of the package to create the new package?

Choose one answer.

	a. Cut the sides in half
	b. Cut the sides in quarters
	c. Cut the sides in eighths
	d. Double the sides

Question 53

Determine the surface area of the shape below.

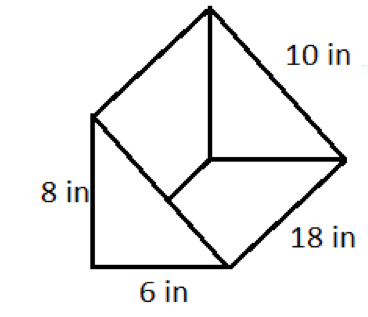
Choose one answer.

	a. 432 in²
	b. 456 in²
	c. 480 in²
	d. 528 in²

Question 54

Determine the volume of the following shape.

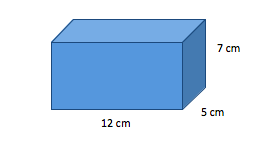
Choose one answer.

	a. 24 cm³
	b. 358 cm³
	c. 420 cm³
	d. 1257 cm³

Question 55

Jerod is building a staircase. He needs to calculate the angles so that the wood will meet the wall correctly. What is the measure of the angle that connects the wall to the top of the staircase?

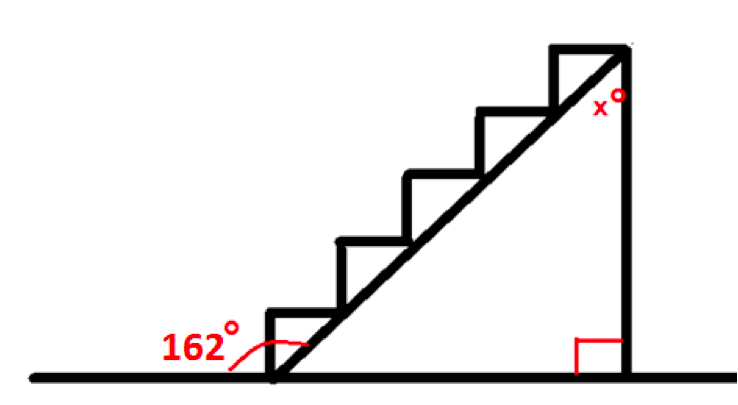
Choose one answer.

	a. 162°
	b. 72°
	c. 62°
	d. 18°

Question 56

Name three lengths that could form a triangle.

Choose one answer.

	a. 5 cm, 6 cm, 9 cm
	b. 3 cm, 8 cm, 14 cm
	c. 3 cm, 3 cm, 14 cm
	d. 1 cm, 10 cm, 12 cm

Question 57

Review the following figure and name the relationship between < 3 and < 4.

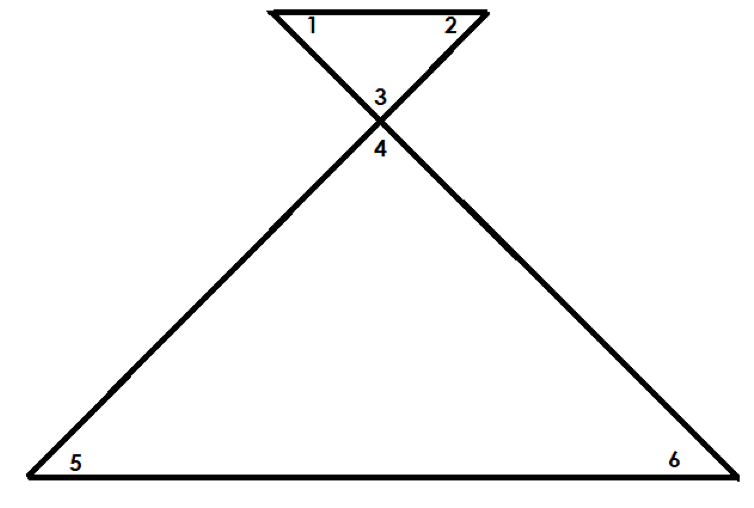
Choose one answer.

	a. Adjacent angles
	b. Supplementary angles
	c. Complementary angles
	d. Vertical angles

Question 58

The area of a triangle is 80 in² and the base is 10 in. What is the height of the triangle?

Choose one answer.

	a. 8 inches
	b. 16 inches
	c. 24 inches
	d. 80 inches

Question 59

The surface area of a cube is 96 cm². What is the volume of the same cube?

Choose one answer.

	a. 4 cm³
	b. 16 cm³
	c. 64 cm³
	d. 256 cm³

Question 60

What is the circumference of a circle with a diameter of 50 m? The answer should be in terms of pi.

Choose one answer.

	a. 50π m
	b. 100π m
	c. 200π m
	d. 2500π m

Question 61

When the perimeter of a square is doubled, which expression explains what happens to the area of the square?

Choose one answer.

	a. The area is also doubled.
	b. The area is cut in half.
	c. The area is quadrupled.
	d. The area is cut in fourths.

Question 62

Which of the following equations could be used to solve for x in the given diagram?

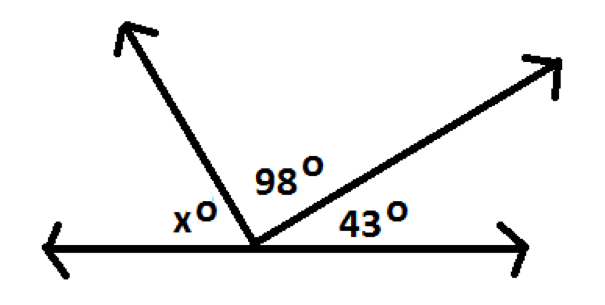
Choose one answer.

	a. 43 + x = 98
	b. 43 + 98 + x = 180
	c. x = 43
	d. 43 + 98 + x = 360

Question 63

Which of the following is an example of a quadrilateral that is impossible to draw?

Choose one answer.

	a. Trapezoid with only two right angles
	b. Parallelogram with obtuse and acute angles
	c. Trapezoid with three right angles
	d. Rhombus with obtuse and acute angles

Question 64

Which of the following shapes can hold more?

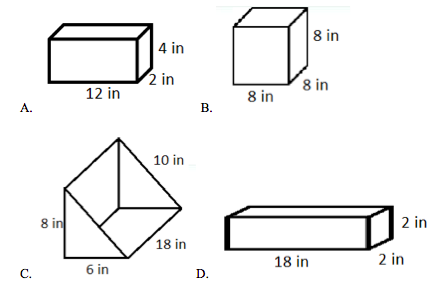
Choose one answer.

	a. A
	b. B
	c. C
	d. D

Question 65

Carlos is developing an experiment to represent people choosing from six different flavors of soup. Which of the following objects could be used to help model the situation?

Choose one answer.

	a. Number cube
	b. Spinner
	c. Deck of cards
	d. Coin

Question 66

Emma made a line plot of all of her grades in math class this month. What are the mean and median of her scores?

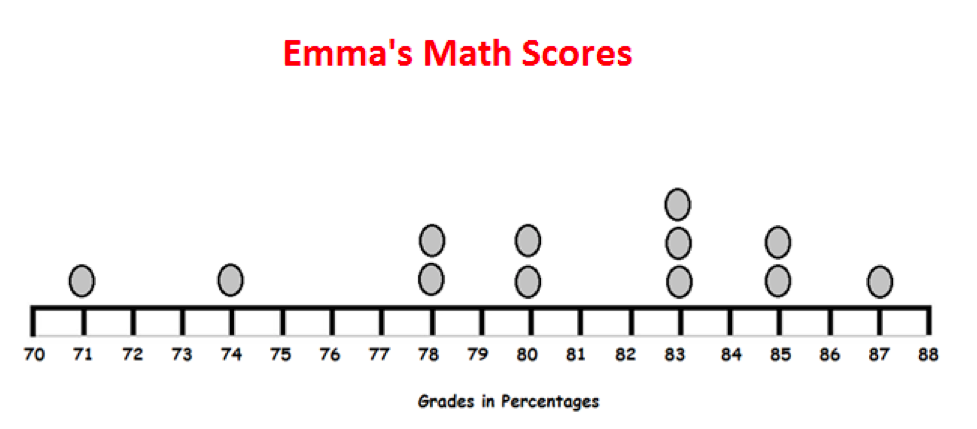
Choose one answer.

	a. Mean = 80.5, median 80
	b. Mean = 80.5, median = 81.5
	c. Mean = 81.5, median = 80.5
	d. Mean = 81.5, median = 83

Question 67

Enoch threw a number cube 600 times. It landed on a number greater than 4, 420 times. Enoch claims that his results were different from what he had predicted. Which of the following expressions explains what Enoch meant?

Choose one answer.

	a. Enoch was expecting to get a number greater than 4 only about 50% of the time and instead he rolled a number greater than 4 70% of the time.
	b. Enoch was expecting to get a number greater than 4 only about 25% of the time and instead he rolled a number greater than 4 70% of the time.
	c. Enoch was expecting to get a number greater than 4 only about 33% of the time and instead he rolled a number greater than 4 70% of the time.
	d. Enoch was expecting to get a number greater than 4 only about 17% of the time and instead he rolled a number greater than 4 70% of the time.

Question 68

Henry has eight cards numbered 1 through 8. He is going to choose two cards from the deck without replacement. What is the probability that he will choose two odd-numbered cards?

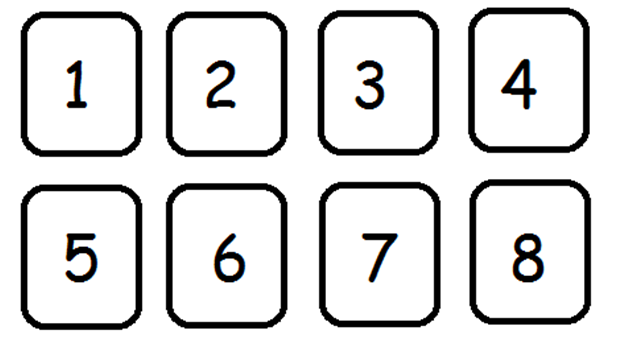
Choose one answer.

	a.
	b.
	c.
	d.

Question 69

How many different possible outcomes are there when a fair coin and a number cube are both tossed at the same time?

Choose one answer.

	a. 2
	b. 8
	c. 12
	d. 36

Question 70

If a fair number cube, labeled with the numbers 1 - 6, is rolled 90 times, which result is most likely to occur?

Choose one answer.

	a. The number cube will land on an odd number about 45 times.
	b. The number cube will land on an odd number exactly 45 times.
	c. The number cube will land on a number larger than 4 about 15 times.
	d. The number cube will land on a number larger than 4 exactly 15 times.

Question 71

Kyla has 100 songs randomly playing in her "wake up" playlist on her MP3 player. Five of those songs are by her favorite artist. What is the probability that one of the next three songs are by her favorite artist?

Choose one answer.

	a. 86%
	b. 45%
	c. 5%
	d. 0.45%

Question 72

Mrs. Colton is in charge of ordering yearbooks. She conducts a survey of 50 students to see who is planning to purchase a yearbook in the spring. Thirty-five of the students indicate that they plan to make the purchase. If there are 1,200 students in the school, how many should Mrs. Colton plan on purchasing a yearbook?

Choose one answer.

	a. 35 students
	b. 420 students
	c. 600 students
	d. 840 students

Question 73

One out of every six students in a seventh-grade class is left-handed. Which of the following could be used to find the experimental probability that we will get a left-handed student when choosing randomly?

Choose one answer.

	a. Use a coin. Heads is right-handed, tails is left-handed.
	b. Use a spinner with four colors. Red represents right-handed. Yellow, blue, and green are left-handed.
	c. Use a number cube. Even numbers represent right-handed and odd numbers represent left-handed.
	d. Use a number cube. Landing on 1 represents left-handed. Landing on 2 - 6 represents-right handed.

Question 74

Sarah and Pardik are comparing the number of home runs per game for each of their baseball teams. Compare the mean absolute deviation (MAD) of number of home runs for the different teams.

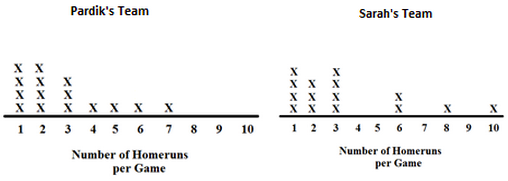
Choose one answer.

	a. Sarah's team has a smaller mean but a larger MAD.
	b. Sarah's team has a smaller mean and a smaller MAD.
	c. Sarah's team has a larger mean but a smaller MAD.
	d. Sarah's team has a larger mean and a larger MAD.

Question 75

Sunil is randomly tossing shoes onto her rug. Using the following graphic, what is the probability that the shoes will land in the center area of the rug?

Choose one answer.

	a.
	b.
	c.
	d.

Question 76

The following box-and-whisker plots show the average daily temperatures in spring and summer. Which of the following describes the variability between the two seasons?

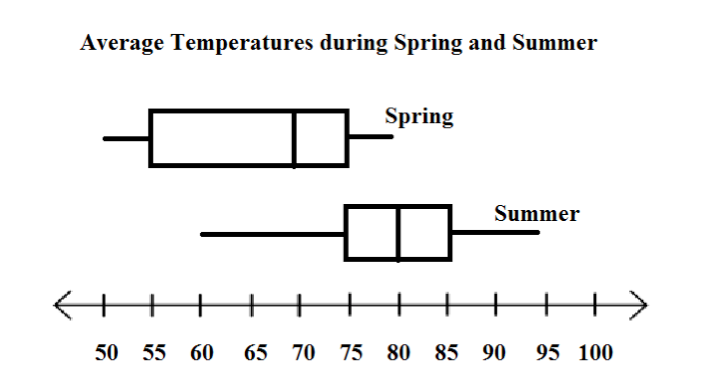
Choose one answer.

	a. The summer season has a smaller range and a smaller interquartile range than the spring season.
	b. The spring has a larger interquartile range; however, the summer has a larger range.
	c. The summer has a smaller MAD and a smaller range than the spring season.
	d. The spring has a larger interquartile range and a larger MAD than the summer season.

Question 77

The net below shows the sides of an unusual number cube. What is the sample space for this number cube?

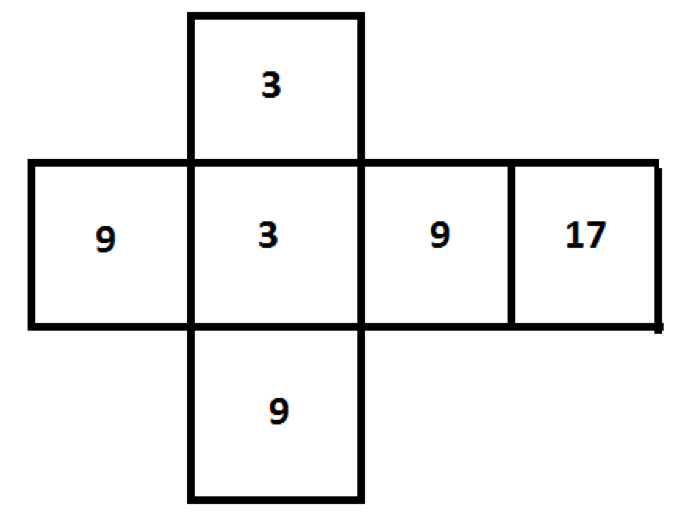
Choose one answer.

	a. {1, 2, 3, 4, 5, 6}
	b. {1, 2, 3}
	c. {3, 3, 9, 9, 9, 17}
	d. {3, 9, 17}

Question 78

Use the table to answer the question. Which of the following math sentences shows how many ways you can make a pizza with one topping?

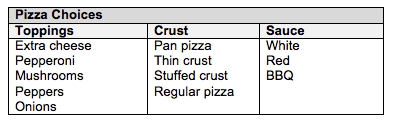
Choose one answer.

	a. 5 + 4 + 3 = 12
	b. 5 x 4 x 3 = 60
	c. (5 + 4) x 3 = 27
	d. (5 x 4) + (5 x 3) = 35

Question 79

What is another name for the interquartile range (IQR)?

Choose one answer.

	a. Mean
	b. Median
	c. Measure of center
	d. Measure of variability

Question 80

Which description explains the diagram below?

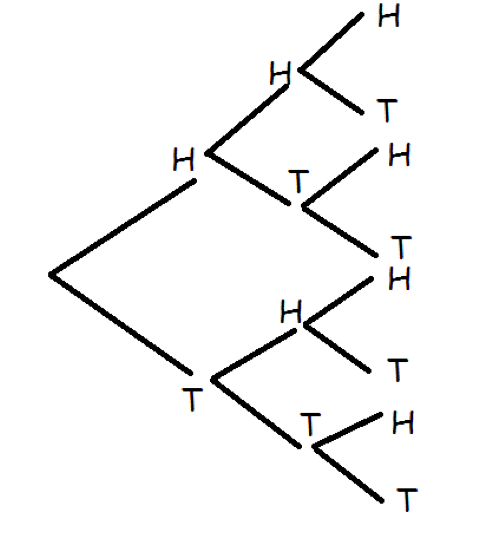
Choose one answer.

	a. Tossing eight coins
	b. Tossing three coins
	c. Tossing a coin eight times
	d. Tossing a coin three times