If we translate an application to a mathematical setup using two variables, then we need to form a linear system with two equations. Setting up word problems with two variables often simplifies the entire process, particularly when the relationships between the variables are not so clear.
The sum of 4 times a larger integer and 5 times a smaller integer is 7. When twice the smaller integer is subtracted from 3 times the larger, the result is 11. Find the integers.
Solution:
Begin by assigning variables to the larger and smaller integer.
Let x represent the larger integer.
Let y represent the smaller integer.
When using two variables, we need to set up two equations. The first sentence describes a sum and the second sentence describes a difference.


This leads to the following system:
Solve using the elimination method. To eliminate the variable y multiply the first equation by 2 and the second by 5.
Add the equations in the equivalent system and solve for x.
Back substitute to find y.
Answer: The larger integer is 3 and the smaller integer is −1.
Try this! An integer is 1 less than twice that of another. If their sum is 20, find the integers.
Answer: The two integers are 7 and 13.
Next consider applications involving simple interest and money.
A total of $12,800 was invested in two accounts. Part was invested in a CD at a annual interest rate and part was invested in a money market fund at a annual interest rate. If the total simple interest for one year was $465, then how much was invested in each account?
Solution:
Begin by identifying two variables.
Let x represent the amount invested at .
Let y represent the amount invested at .
The total amount in both accounts can be expressed as
To set up a second equation, use the fact that the total interest was $465. Recall that the interest for one year is the interest rate times the principal (). Use this to add the interest in both accounts. Be sure to use the decimal equivalents for the interest rates given as percentages.
These two equations together form the following linear system:
Eliminate x by multiplying the first equation by −0.03125.
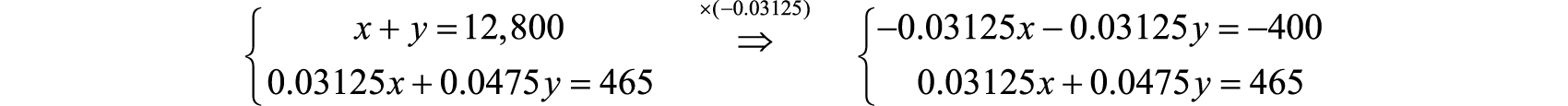
Next, add the resulting equations.
Back substitute to find x.
Answer: $4,000 was invested at and $8,800 was invested at .
A jar consisting of only nickels and dimes contains 58 coins. If the total value is $4.20, how many of each coin is in the jar?
Solution:
Let n represent the number of nickels in the jar.
Let d represent the number of dimes in the jar.
The total number of coins in the jar can be expressed using the following equation:
Next, use the value of each coin to determine the total value $4.20.
This leads us to following linear system:
Here we will solve using the substitution method. In the first equation, we can solve for n.

Substitute into the second equation and solve for d.
Now back substitute to find the number of nickels.
Answer: There are 32 nickels and 26 dimes in the jar.
Try this! Joey has a jar full of 40 coins consisting of only quarters and nickels. If the total value is $5.00, how many of each coin does Joey have?
Answer: Joey has 15 quarters and 25 nickels.
Mixture problems often include a percentage and some total amount. It is important to make a distinction between these two types of quantities. For example, if a problem states that a 20-ounce container is filled with a 2% saline (salt) solution, then this means that the container is filled with a mixture of salt and water as follows:
|
Percentage |
Amount |
|---|---|---|
Salt |
2% = 0.02 |
0.02(20 ounces) = 0.4 ounces |
Water |
98% = 0.98 |
0.98(20 ounces) = 19.6 ounces |
In other words, we multiply the percentage times the total to get the amount of each part of the mixture.
A 1.8% saline solution is to be combined and mixed with a 3.2% saline solution to produce 35 ounces of a 2.2% saline solution. How much of each is needed?
Solution:
Let x represent the amount of 1.8% saline solution needed.
Let y represent the amount of 3.2% saline solution needed.
The total amount of saline solution needed is 35 ounces. This leads to one equation,
The second equation adds up the amount of salt in the correct percentages. The amount of salt is obtained by multiplying the percentage times the amount, where the variables x and y represent the amounts of the solutions. The amount of salt in the end solution is 2.2% of the 35 ounces, or .022(35).
The algebraic setup consists of both equations presented as a system:
Solve.
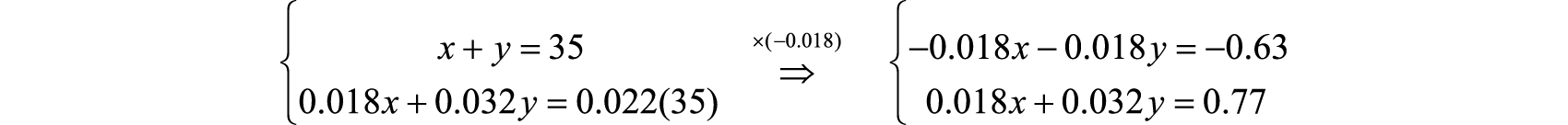
Add the resulting equations together
Back substitute to find x.
Answer: We need 25 ounces of the 1.8% saline solution and 10 ounces of the 3.2% saline solution.
An 80% antifreeze concentrate is to be mixed with water to produce a 48-liter mixture containing 25% antifreeze. How much water and antifreeze concentrate is needed?
Solution:
Let x represent the amount of 80% antifreeze concentrate needed.
Let y represent the amount of water needed.
The total amount of the mixture must be 48 liters.
The second equation adds up the amount of antifreeze from each solution in the correct percentages. The amount of antifreeze in the end result is 25% of 48 liters, or 0.25(48).
Now we can form a system of two linear equations and two variables as follows:
Use the second equation to find x:
Back substitute to find y.
Answer: We need to mix 33 liters of water with 15 liters of antifreeze concentrate.
Try this! A chemist wishes to create 100 ml of a solution with 12% acid content. He uses two types of stock solutions, one with 30% acid content and another with 10% acid content. How much of each does he need?
Answer: The chemist will need to mix 10 ml of the 30% acid solution with 90 ml of the 10% acid solution.
Recall that the distance traveled is equal to the average rate times the time traveled at that rate, . These uniform motion problems usually have a lot of data, so it helps to first organize that data in a chart and then set up a linear system. In this section, you are encouraged to use two variables.
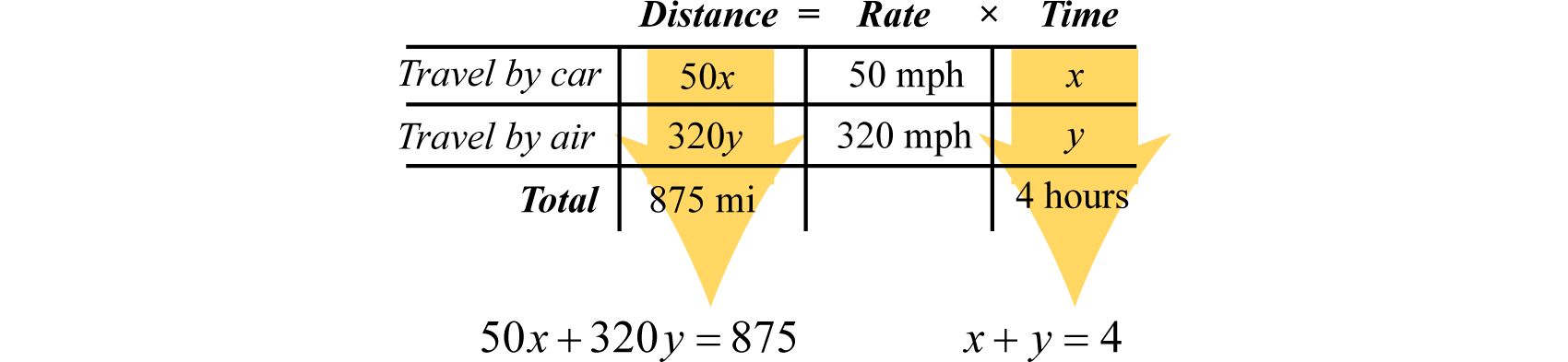
An executive traveled a total of 4 hours and 875 miles by car and by plane. Driving to the airport by car, she averaged 50 miles per hour. In the air, the plane averaged 320 miles per hour. How long did it take her to drive to the airport?
Solution:
We are asked to find the time it takes her to drive to the airport; this indicates that time is the unknown quantity.
Let x represent the time it took to drive to the airport.
Let y represent the time spent in the air.
Fill in the chart with the given information.

Use the formula to fill in the unknown distances.

The distance column and the time column of the chart help us to set up the following linear system.
Solve.
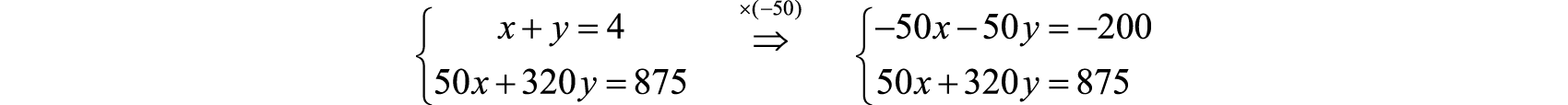
Now back substitute to find the time x it took to drive to the airport:
Answer: It took her hours to drive to the airport.
It is not always the case that time is the unknown quantity. Read the problem carefully and identify what you are asked to find; this defines your variables.
Applications involving simple interest and money.
Applications involving a mixture of amounts usually given as a percentage of some total.
Applications relating distance, average rate, and time.
Flying with the wind, a light aircraft traveled 240 miles in 2 hours. The aircraft then turned against the wind and traveled another 135 miles in hours. Find the speed of the airplane and the speed of the wind.
Solution:
Begin by identifying variables.
Let x represent the speed of the airplane.
Let w represent the speed of the wind.
Use the following chart to organize the data:

With the wind, the airplane’s total speed is . Flying against the wind, the total speed is .

Use the rows of the chart along with the formula to construct a linear system that models this problem. Take care to group the quantities that represent the rate in parentheses.

If we divide both sides of the first equation by 2 and both sides of the second equation by 1.5, then we obtain the following equivalent system:
Here w is lined up to eliminate.
Back substitute.
Answer: The speed of the airplane is 105 miles per hour and the speed of the wind is 15 miles per hour.
Try this! A boat traveled 27 miles downstream in 2 hours. On the return trip, which was against the current, the boat was only able to travel 21 miles in 2 hours. What were the speeds of the boat and of the current?
Answer: The speed of the boat was 12 miles per hour and the speed of the current was 1.5 miles per hour.
Set up a linear system and solve.
The sum of two integers is 45. The larger integer is 3 less than twice the smaller. Find the two integers.
The sum of two integers is 126. The larger is 18 less than 5 times the smaller. Find the two integers.
The sum of two integers is 41. When 3 times the smaller is subtracted from the larger the result is 17. Find the two integers.
The sum of two integers is 46. When the larger is subtracted from twice the smaller the result is 2. Find the two integers.
The difference of two integers is 11. When twice the larger is subtracted from 3 times the smaller, the result is 3. Find the integers.
The difference of two integers is 6. The sum of twice the smaller and the larger is 72. Find the integers.
The sum of 3 times a larger integer and 2 times a smaller is 15. When 3 times the smaller integer is subtracted from twice the larger, the result is 23. Find the integers.
The sum of twice a larger integer and 3 times a smaller is 10. When the 4 times the smaller integer is added to the larger, the result is 0. Find the integers.
The difference of twice a smaller integer and 7 times a larger is 4. When 5 times the larger integer is subtracted from 3 times the smaller, the result is −5. Find the integers.
The difference of a smaller integer and twice a larger is 0. When 3 times the larger integer is subtracted from 2 times the smaller, the result is −5. Find the integers.
The length of a rectangle is 5 more than twice its width. If the perimeter measures 46 meters, then find the dimensions of the rectangle.
The width of a rectangle is 2 centimeters less than one-half its length. If the perimeter measures 62 centimeters, then find the dimensions of the rectangle.
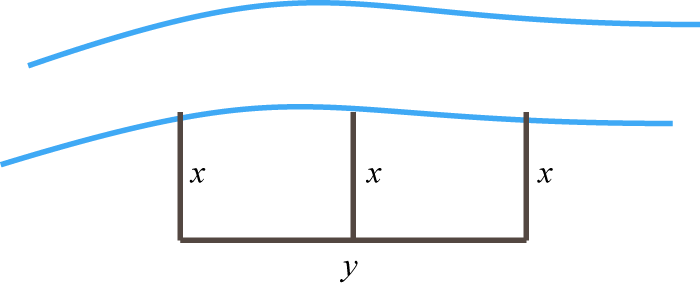
A partitioned rectangular pen next to a river is constructed with a total 136 feet of fencing (see illustration). If the outer fencing measures 114 feet, then find the dimensions of the pen.
A partitioned rectangular pen is constructed with a total 168 feet of fencing (see illustration). If the perimeter measures 138 feet, then find the dimensions of the pen.

Find a and b such that the system has solution . (Hint: Substitute the given x- and y-values and solve the resulting linear system in terms of a and b.)
Find a and b such that the system has solution .
A line passes through two points and . Use these points and to construct a system of two linear equations in terms of m and b and solve it.
A line passes through two points and . Use these points and to construct a system of two linear equations in terms of m and b and solve it.
A $5,200 principal is invested in two accounts, one earning 3% interest and another earning 6% interest. If the total interest for the year is $210, then how much is invested in each account?
Harry’s $2,200 savings is in two accounts. One account earns 2% annual interest and the other earns 4%. His total interest for the year is $69. How much does he have in each account?
Janine has two savings accounts totaling $6,500. One account earns annual interest and the other earns . If her total interest for the year is $211, then how much is in each account?
Margaret has her total savings of $24,200 in two different CD accounts. One CD earns 4.6% interest and another earns 3.4% interest. If her total interest for the year is $1,007.60, then how much does she have in each CD account?
Last year Mandy earned twice as much interest in her Money Market fund as she did in her regular savings account. The total interest from the two accounts was $246. How much interest did she earn in each account?
A small business invested $120,000 in two accounts. The account earning 4% annual interest yielded twice as much interest as the account earning 3% annual interest. How much was invested in each account?
Sally earns $1,000 per month plus a commission of 2% of sales. Jane earns $200 per month plus 6% of her sales. At what monthly sales figure will both Sally and Jane earn the same amount of pay?
The cost of producing specialty book shelves includes an initial set-up fee of $1,200 plus an additional $20 per unit produced. Each shelf can be sold for $60 per unit. Find the number of units that must be produced and sold where the costs equal the revenue generated.
Jim was able to purchase a pizza for $12.35 with quarters and dimes. If he uses 71 coins to buy the pizza, then how many of each did he have?
A cash register contains $5 bills and $10 bills with a total value of $350. If there are 46 bills total, then how many of each does the register contain?
Two families bought tickets for the home basketball game. One family ordered 2 adult tickets and 4 children’s tickets for a total of $36.00. Another family ordered 3 adult tickets and 2 children’s tickets for a total of $32.00. How much did each ticket cost?
Two friends found shirts and shorts on sale at a flea market. One bought 4 shirts and 2 shorts for a total of $28.00. The other bought 3 shirts and 3 shorts for a total of $30.75. How much was each shirt and each pair of shorts?
A community theater sold 140 tickets to the evening musical for a total of $1,540. Each adult ticket was sold for $12 and each child ticket was sold for $8. How many adult tickets were sold?
The campus bookstore sells graphing calculators for $110 and scientific calculators for $16. On the first day of classes 50 calculators were sold for a total of $1,646. How many of each were sold?
A jar consisting of only nickels and quarters contains 70 coins. If the total value is $9.10, how many of each coin are in the jar?
Jill has $9.20 worth of dimes and quarters. If there are 68 coins in total, how many of each does she have?
Set up a linear system and solve.
A 17% acid solution is to be mixed with a 9% acid solution to produce 8 gallons of a 10% acid solution. How much of each is needed?
A nurse wishes to obtain 28 ounces of a 1.5% saline solution. How much of a 1% saline solution must she mix with a 4.5% saline solution to achieve the desired mixture?
A customer ordered 4 pounds of a mixed peanut product containing 12% cashews. The inventory consists of only two mixes containing 10% and 26% cashews. How much of each type must be mixed to fill the order?
One alcohol solution contains 10% alcohol and another contains 25% alcohol. How much of each should be mixed together to obtain 2 gallons of a 13.75% alcohol solution?
How much cleaning fluid concentrate, with 60% alcohol content, must be mixed with water to obtain a 24-ounce mixture with 15% alcohol content?
How many pounds of pure peanuts must be combined with a 20% peanut mix to produce 2 pounds of a 50% peanut mix?
A 50% fruit juice concentrate can be purchased wholesale. Best taste is achieved when water is mixed with the concentrate in such a way as to obtain a 15% fruit juice mixture. How much water and concentrate is needed to make a 60-ounce fruit juice drink?
Pure sugar is to be mixed with a fruit salad containing 10% sugar to produce 65 ounces of a salad containing 18% sugar. How much pure sugar is required?
A custom aluminum alloy is created by mixing 150 grams of a 15% aluminum alloy and 350 grams of a 55% aluminum alloy. What percentage of aluminum is in the resulting mixture?
A research assistant mixed 500 milliliters of a solution that contained a 12% acid with 300 milliliters of water. What percentage of acid is in the resulting solution?
Set up a linear system and solve.
The two legs of a 432-mile trip took 8 hours. The average speed for the first leg of the trip was 52 miles per hour and the average speed for the second leg of the trip was 60 miles per hour. How long did each leg of the trip take?
Jerry took two buses on the 265-mile trip from Los Angeles to Las Vegas. The first bus averaged 55 miles per hour and the second bus was able to average 50 miles per hour. If the total trip took 5 hours, then how long was spent in each bus?
An executive was able to average 48 miles per hour to the airport in her car and then board an airplane that averaged 210 miles per hour. The 549-mile business trip took 3 hours. How long did it take her to drive to the airport?
Joe spends 1 hour each morning exercising by jogging and then cycling for a total of 15 miles. He is able to average 6 miles per hour jogging and 18 miles per hour cycling. How long does he spend jogging each morning?
Swimming with the current Jack can swim 2.5 miles in hour. Swimming back, against the same current, he can only swim 2 miles in the same amount of time. How fast is the current?
A light aircraft flying with the wind can travel 180 miles in hours. The aircraft can fly the same distance against the wind in 2 hours. Find the speed of the wind.
A light airplane flying with the wind can travel 600 miles in 4 hours. On the return trip, against the wind, it will take 5 hours. What are the speeds of the airplane and of the wind?
A boat can travel 15 miles with the current downstream in hours. Returning upstream against the current, the boat can only travel miles in the same amount of time. Find the speed of the current.
Mary jogged the trail from her car to the cabin at the rate of 6 miles per hour. She then walked back to her car at a rate of 4 miles per hour. If the entire trip took 1 hour, then how long did it take her to walk back to her car?
Two trains leave the station traveling in opposite directions. One train is 8 miles per hour faster than the other and in hours they are 230 miles apart. Determine the average speed of each train.
Two trains leave the station traveling in opposite directions. One train is 12 miles per hour faster than the other and in 3 hours they are 300 miles apart. Determine the average speed of each train.
A jogger can sustain an average running rate of 8 miles per hour to his destination and 6 miles an hour on the return trip. Find the total distance the jogger ran if the total time running was hour.
Compose a number or money problem of your own and share it on the discussion board.
Compose a mixture problem of your own and share it on the discussion board.
Compose a uniform motion problem of your own and share it on the discussion board.
The integers are 16 and 29.
The integers are 6 and 35.
The integers are 25 and 36.
The integers are −3 and 7.
The integers are −5 and −2.
Length: 17 meters; width: 6 meters
Width: 22 feet; length: 70 feet
,
,
$3,400 at 3% and $1,800 at 6%
$2,200 at and $4,300 at
Savings: $82; Money Market: $164.
$20,000
35 quarters and 36 dimes
Adults $7.00 each and children $5.50 each.
105 adult tickets were sold.
The jar contains 42 nickels and 28 quarters.
7 gallons of the 9% acid solution and 1 gallon of the 17% acid solution
3.5 pounds of the 10% cashew mix and 0.5 pounds of the 26% cashew mix
6 ounces of cleaning fluid concentrate
18 ounces of fruit juice concentrate and 42 ounces of water
43%
The first leg of the trip took 6 hours and the second leg took 2 hours.
It took her hour to drive to the airport.
0.5 miles per hour.
Airplane: 135 miles per hour; wind: 15 miles per hour
hour
One train averaged 44 miles per hour and the other averaged 56 miles per hour.
Answer may vary
Answer may vary