When we think of auctions, we tend to think of movies where people scratch their ear and accidentally purchase a Fabergé egg. However, stock exchanges, bond markets, and commodities markets are organized as auctions, too, and because of such exchanges, auctions are the most common means of establishing prices. Auctions are one of the oldest transactions means recorded in human history; they were used by the Babylonians. The word auction comes from the Latin auctio, meaning “to increase.”
Auctions have been used to sell a large variety of things. Internet auction house eBay is most famous for weird items that have been auctioned (for example, one person’s attempt to sell her soul), but in addition, many of the purchases of the U.S. government are made by auction. The United States purchases everything from fighter aircraft to french fries by auction, and the U.S. government is the world’s largest purchaser of french fries. In addition, corporations are occasionally sold by auction. Items that are usually sold by auction include prize bulls, tobacco, used cars, race horses, coins, stamps, antiques, and fine art.
An English auctionAuction where bids increase until no one is willing to top the current bid. is the common auction form used for selling antiques, art, used cars, and cattle. The auctioneer starts low and calls out prices until no bidder is willing to bid higher than the current high price. The most common procedure is for a low price to be called out and a bidder to accept it. A higher price is called out, and a different bidder accepts it. When several accept simultaneously, the auctioneer accepts the first one spotted. This process continues until a price is called out that no one accepts. At that point, the auction ends, and the highest bidder wins.
Information plays a significant role in bidding in auctions. The two major extremes in information, which lead to distinct theories, are private valuesSituation in which bidders in an auction know their own value., which means bidders know their own value, and common valuesSituation in which bidders in an auction have the same value, which is generally not known with certainty., in which bidders don’t know their own value but have some indication or signal about the value. In the private values situation, a bidder may be outbid by another bidder but doesn’t learn anything from another bidder’s willingness to pay. The case of private values arises when the good being sold has a quality apparent to all bidders, no hidden attributes, and no possibility of resale. In contrast, the case of common values arises when bidders don’t know the value of the item for sale, but that value is common to all. The quintessential example is an offshore oil lease. No one knows for sure how much oil can be extracted from an offshore lease, and companies have estimates of the amount of oil. The estimates are closely guarded because rivals could learn from them. Similarly, when antiques dealers bid on an antique, the value they place on it is primarily the resale value. Knowing rivals’ estimates of the resale value could influence the value each bidder placed on the item.
The private values environment is unrealistic in most settings because items for sale usually have some element of common value. However, some situations approximate the private values environment and these are the most easy to understand.
In a private values setting, a very simple bidding strategy is optimal for bidders: a bidder should keep bidding until the price exceeds the value a bidder places on it, at which point the bidder should stop. That is, bidders should drop out of the bidding when the price exceeds their value because at that point, winning the auction requires the bidder to take a loss. Every bidder should be willing to continue to bid to prevent someone else from winning the auction provided the price is less than the bidder’s value. If you have a value v and another bidder is about to win at a price pa < v, you might as well accept a price pb between the two, pa < pb < v because a purchase at this price would provide you with a profit. This strategy is a dominant strategy for each private values bidder because no matter what strategy the other bidders adopt, bidding up to value is the strategy that maximizes the profit for each bidder.
The presence of a dominant strategy makes it easy to bid in the private values environment. In addition, it simplifies the analysis of the English auction relatively simple.
Most auctioneers use a flexible system of bid incrementsThe difference between successive price requests.. A bid increment is the difference between successive price requests. The theory is simplest when the bid increment, denoted by δ, is very small. In this case, the bidder with the highest value wins, and the price is no more than the second-highest value, but it is at least the second-highest value minus δ, because a lower price would induce the bidder with the second-highest value to submit a slightly higher bid. If we denote the second-highest value with the somewhat obscure (but standard) notation v(2), the final price p satisfies
As the bid increment gets small, the price is nailed down. The conclusion is that, when bid increments are small and bidders have private values, the bidder with the highest value wins the bidding at a price equal to the second-highest value. The notation for the highest value is v(1), and thus the seller obtains v(2), and the winning bidder obtains profits of v(1) – v(2).
In a sealed-bid auctionAuction where bidders simultaneously submit sealed bids, and the highest bidder wins and pays the highest bid., each bidder submits a bid in an envelope. These are opened simultaneously, and the highest bidder wins the item and pays his or her bid. Sealed-bid auctions are used to sell offshore oil leases, and they are used by governments to purchase a wide variety of items. In a purchase situation, known often as a tender, the lowest bidder wins the amount he bids.
The analysis of the sealed-bid auction is more challenging because the bidders don’t have a dominant strategy. Indeed, the best bid depends on what the other bidders are bidding. The bidder with the highest value would like to bid a penny more than the next highest bidder’s bid, whatever that might be.
To pursue an analysis of the sealed-bid auction, we are going to make a variety of simplifying assumptions. These assumptions aren’t necessary to the analysis, but we make them to simplify the mathematical presentation.
We suppose there are n bidders, and we label the bidders 1, …, n. Bidder i has a private value vi, which is a draw from the uniform distribution on the interval [0,1]. That is, if the probability that bidder i’s value is in the interval [a, b] is b – a. An important attribute of this assumption is symmetry—the bidders all have the same distribution. In addition, the formulation has assumed independence—the value one bidder places on the object for sale is statistically independent from the value placed by others. Each bidder knows his own value but he doesn’t know the other bidders’ values. Each bidder is assumed to bid in such a way as to maximize his expected profit (we will look for a Nash equilibrium of the bidding game). Bidders are permitted to submit any bid equal to or greater than zero.
To find an equilibrium, it is helpful to restrict attention to linear strategies, in which a bidder bids a proportion of her value. Thus, we suppose that each bidder bids λv when her value is v and λ is a positive constant, usually between zero and one. With this set up we shall examine under what conditions these strategies comprise a Nash equilibrium. An equilibrium exists when all other bidders bid λv when their value is v, and the remaining bidders bid the same.
So fix a bidder and suppose that bidder’s value is vi. What bid should the bidder choose? A bid of b wins the bidding if all other bidders bid less than b. Because the other bidders, by hypothesis, bid λv when their value is v, our bidder wins when for each other bidder j. This occurs when for each other bidder j, and this in turn occurs with probability If then in fact the probability is 1. You can show that no bidder would ever bid more than λ. Thus, our bidder with value vi who bids b wins with probability because the bidder must beat all n −1 other bidders. That creates expected profits for the bidder of
The bidder chooses b to maximize expected profits. The first-order condition requires
The first-order condition solves for
But this is a linear rule. Thus, if we have a Nash equilibrium.
The nature of this equilibrium is that each bidder bids a fraction of his value, and the highest-value bidder wins at a price equal to that fraction of her value.
In some cases, the sealed-bid auction produces regret. Regret means that a bidder wishes she had bid differently. Recall our notation for values: v(1) is the highest value and v(2) is the second-highest value. Because the price in a sealed-bid auction is the second-highest bidder will regret her bid when In this case, the bidder with the second-highest value could have bid higher and won, if the bidder had known the winning bidder’s bid. In contrast, the English auction is regret-free: the price rises to the point that the bidder with the second-highest value won’t pay.
How do the two auctions compare in prices? It turns out that statistical independence of private values implies revenue equivalenceSituation in which two auctions produce the same price on average., which means the two auctions produce the same prices on average. Given the highest value v(1), the second-highest value has distribution because this is the probability that all n − 1 other bidders have values less than v(2). But this gives an expected value of v(2) of
Thus, the average price paid in the sealed-bid auction is the same as the average price in the English auction.
The Dutch auctionAuction where prices start high and decrease until a bidder signals willingness to pay, at which point the auction stops. is like an English auction, except that prices start high and are successively dropped until a bidder accepts the going price, and the auction ends. The Dutch auction is so-named because it is used to sell cut flowers in Holland, in the enormous flower auctions.
A strategy in a Dutch auction is a price at which the bidder bids. Each bidder watches the price decline, until it reaches such a point that either the bidder bids or a rival bids, and the auction ends. Note that a bidder could revise his bid in the course of the auction, but there isn’t any reason to do so. For example, suppose the price starts at $1,000, and a bidder decides to bid when the price reaches $400. Once the price gets to $450, the bidder could decide to revise and wait until $350. However, no new information has become available and there is no reason to revise. In order for the price to reach the original planned bid of $400, it had to reach $450, meaning that no one bid prior to a price of $450. In order for a bid of $400 to win, the price had to reach $450; if the price reaching $450 means that a bid of $350 is optimal, then the original bid of $400 could not have been optimal.Of course, a bidder who thinks losing is likely may wait for a lower price to formulate the bid, a consideration ignored here. In addition, because the Dutch auction unfolds over time, bidders who discount the future will bid slightly higher in a Dutch auction as a way of speeding it along, another small effect that is ignored for simplicity.
What is interesting about the Dutch auction is that it has exactly the same possible strategies and outcomes as the sealed-bid auction. In both cases, a strategy for a bidder is a bid, no bidder sees the others’ bids until after her own bid is formulated, and the winning bidder is the one with the highest bid. This is called strategic equivalenceSituation in which two games are strategically equivalent if they have the same strategies (after a renaming) and the strategies lead to the same outcomes.. Both games—the Dutch auction and the sealed-bid auction—offer identical strategies to the bidders and, given the strategies chosen by all bidders, produce the same payoff. Such games should produce the same outcomes.
The strategic equivalence of the Dutch auction and the sealed-bid auction is a very general result that doesn’t depend on the nature of the values of the bidders (private vs. common) or the distribution of information (independent vs. correlated). Indeed, the prediction that the two games should produce the same outcome doesn’t even depend on risk aversion, although that is more challenging to demonstrate.
The strategic equivalence of the Dutch and sealed-bid auction suggests another fact: there may be more than one way of implementing a given kind of auction. Such logic led Nobel laureate William Vickrey (1914–1996) to design what has become known as the Vickrey auctionAuction where bidders bid simultaneously, and the highest bidder wins and pays the second-highest bid., which is a second-price, sealed-bid auction. This auction is most familiar because it is the foundation of eBay’s auction design. The Vickrey auction is a sealed-bid auction, but with a twist: the high bidder wins but pays the second-highest bid. This is why the Vickrey auction is called a second-price auction: the price is not the highest bid, but the second-highest bid.
The Vickrey auction underlies the eBay outcome because when a bidder submits a bid in the eBay auction, the current “going” price is not the highest bid, but the second-highest bid plus a bid increment. Thus, up to the granularity of the bid increment, the basic eBay auction is a Vickrey auction run over time.
As in the English auction, bidders with private values in a Vickrey auction have a dominant strategy. Fix a bidder, with value v, and let p be the highest bid of the other bidders. If the bidder bids b, the bidder earns profits of
It is profitable for the bidder to win if v > p and to lose if v < p. To win when v > p and to lose if v < p can be assured by bidding v. Essentially, there is no gain to bidding less than your value because your bid doesn’t affect the price, only the likelihood of winning. Bidding less than value causes the bidder to lose when the highest rival bid falls between the bid and the value, which is a circumstance that the bidder would like to win. Similarly, bidding more than value creates a chance of winning only when the price is higher than the bidder’s value, in which case the bidder would prefer to lose.
Thus, bidders in a Vickrey auction have a dominant strategy to bid their value. This produces the same outcome as in the English auction, however, because the payment made is the second-highest value, which was the price in the English auction. Thus, the Vickrey auction is a sealed-bid implementation of the English auction when bidders have private values, producing the same outcome, which is that the highest-value bidder wins but pays the second-highest value.
Because the Vickrey auction induces bidders to bid their value, it is said to be demand revealing. Unlike the English auction, in which the bidding stops when the price reaches the second-highest value and thus doesn’t reveal the highest value, the Vickrey auction reveals the highest value. In a controlled, laboratory setting, demand revelation is useful, especially when the goal is to identify buyer values. Despite its theoretical niceties, the Vickrey auction can be politically disastrous. Indeed, New Zealand sold radio spectrum with the Vickrey auction on the basis of advice by a naïve economist, and the Vickrey auction created a political nightmare when a nationwide cellular license received a high bid of $110 million and a second-highest bid of $11 million. The political problem was that the demand revelation showed that the government received only about 10% of the value of the license, making the public quite irate. The situation dominated news coverage at the time.The Vickrey auction generally produces higher prices than regular sealed-bid auctions if bidders are symmetric (that is, share the same distribution of values), but it is a poor choice of auction format when bidders are not symmetric. Because the incumbent telephone company was expected to have a higher value than others, the Vickrey auction was a poor choice for that reason as well. Some smaller licenses sold for tenths of 1% of the highest bid.
In a private values setting, the Vickrey auction and the English auction are much easier on bidders than a regular sealed-bid auction because of the dominant strategy. The sealed-bid auction requires bidders to forecast their rivals’ likely bids and produces the risks of either bidding more than necessary or losing the bidding. Thus, the regular sealed-bid auction has undesirable properties. Moreover, bidders in the sealed-bid auction have an incentive to bribe the auctioneer to reveal the best bid by rivals because that is useful information in formulating a bid. Such (illegal) bribery occurs from time to time in government contracting.
On the other hand, the regular sealed-bid auction has an advantage over the other two because it makes price fixing more difficult. A bidder can cheat on a conspiracy and not be detected until after the current auction is complete.
Another disadvantage of the sealed-bid auction is that it is easier to make certain kinds of bidding errors. In the U.S. PCS auctions, in which rights to use the radio spectrum for cellular phones was sold for around $20 billion, one bidder, intending to bid $200,000, inadvertently bid $200,000,000. Such an error isn’t possible in an English auction because prices rise at a measured pace. And such an error has little consequence in a Vickrey auction because getting the price wrong by an order of magnitude requires two bidders to make such errors.
I paid too much for it, but it's worth it.
Sam Goldwyn
The analysis so far has been conducted under the restrictive assumption of private values. In most contexts, bidders are not sure of the actual value of the item being sold, and information held by others is relevant to the valuation of the item. If I estimate an antique to be worth $5,000, but no one else is willing to bid more than $1,000, I might revise my estimate of the value down. This revision leads bidders to learn from the auction itself what the item is worth.
The early bidders in the sale of oil lease rights in the Gulf of Mexico (the outer continental shelf) were often observed to pay more than the rights were worth. This phenomenon came to be known as the winner’s curseThe bidder who most overestimates the value of the object wins the bidding.. The winner’s curse is the fact that the bidder who most overestimates the value of the object wins the bidding.
Naïve bidders who don’t adjust for the winner’s curse tend to lose money because they win the bidding only when they’ve bid too high.
Figure 20.1 Normally Distributed Estimates
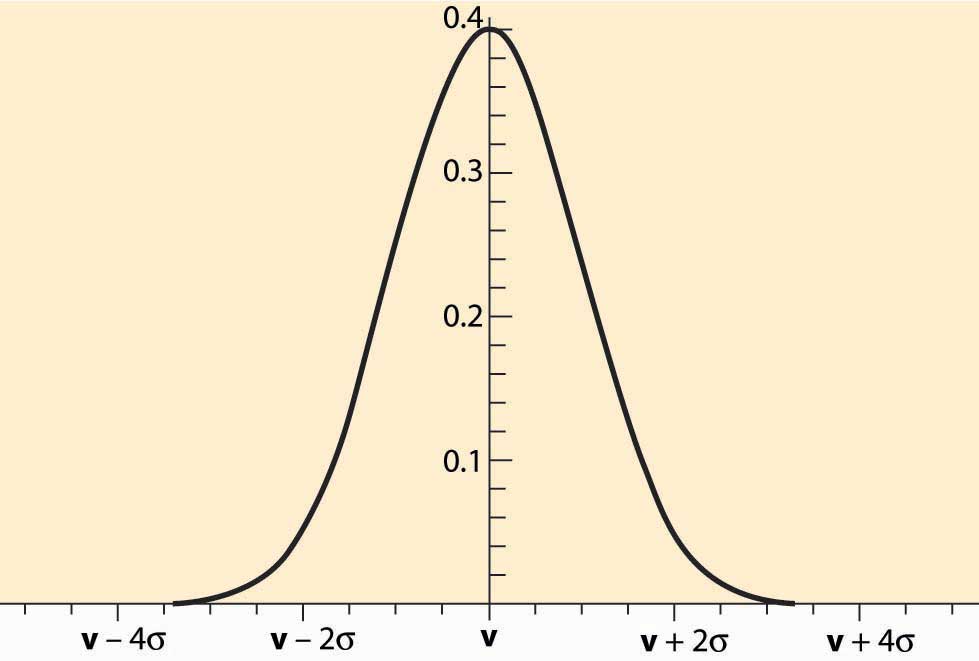
Auctions, by their nature, select optimistic bidders. Consider the case of an oil lease (right to drill for and pump oil) that has an unknown value v. Different bidders will obtain different estimates of the value, and we may view these estimates as draws from a normal distribution, like the one illustrated in Figure 20.1 "Normally Distributed Estimates". The estimates are correct on average, which is represented by the fact that the distribution is centered on the true value v. Thus, a randomly chosen bidder will have an estimate that is too high as often as it is too low, and the average estimate of a randomly selected bidder will be correct. However, the winner of an auction will tend to be the bidder with the highest estimate, not a randomly chosen bidder. The highest of five bidders will have an estimate that is too large 97% of the time. The only way the highest estimate is not too large is if all the estimates are below the true value. With 10 bidders, the highest estimate is larger than the true value with probability 99.9% because the odds that all the estimates are less than the true value is (½)10 = 0.1%. This phenomenon—that auctions tend to select the bidder with the highest estimate, and the highest estimate is larger than the true value most of the time—is characteristic of the winner’s curse.
A savvy bidder corrects for the winner’s curse. Such a correction is actually quite straightforward when a few facts are available, and here a simplified presentation is given. Suppose there are n bidders for a common value good, and the bidders receive normally distributed estimates that are correct on average. Let σ be the standard deviation of the estimates.The standard deviation is a measure of the dispersion of the distribution and is the square root of the average of the square of the difference of the random value and its mean. The estimates are also assumed to be independently distributed around the true value. Note that estimating the mean adds an additional layer of complexity. Finally, suppose that no prior information is given about the likely value of the good.
In this case, it is a straightforward matter to compute a correction for the winner’s curse. Because the winning bidder will generally be the bidder with the highest estimate of value, the winner’s curse correction should be the expected amount by which the highest value exceeds the average value. This can be looked up in a table for the normal distribution. The values are given for selected numbers n in Table 20.1 "Winner’s Curse Correction". This table shows, as a function of the number of bidders, how much each bidder should reduce his estimate of value to correct for the fact that auctions select optimistic bidders. The units are standard deviations.
Table 20.1 Winner’s Curse Correction
| n | 1 | 2 | 3 | 4 | 5 | 10 | 15 |
|---|---|---|---|---|---|---|---|
| WCC (σ) | 0 | .56 | .85 | 1.03 | 1.16 | 1.54 | 1.74 |
| n | 20 | 25 | 50 | 100 | 500 | 1000 | 10,000 |
| WCC (σ) | 1.87 | 1.97 | 2.25 | 2.51 | 3.04 | 3.24 | 3.85 |
For example, with one bidder, there is no correction because it was supposed that the estimates are right on average. With two bidders, the winner’s curse correction is the amount that the higher of two will be above the mean, which turns out to be 0.56σ, a little more than half a standard deviation. This is the amount that should be subtracted from the estimate to ensure that, when the bidder wins, the estimated value is correct, on average. With four bidders, the highest is a bit over a whole standard deviation. As is apparent from the table, the winner’s curse correction increases relatively slowly after 10 or 15 bidders. With a million bidders, it is 4.86σ.
The standard deviation σ measures how much randomness or noise there is in the estimates. It is a measure of the average difference between the true value and the estimated value, and thus the average level of error. Oil companies know from their history of estimation how much error arises in the company estimates. Thus, they can correct their estimates to account for the winner’s curse using their historical inaccuracies.
Bidders who are imperfectly informed about the value of an item for sale are subject to losses arising from the way auctions select the winning bidder. The winning bidder is usually the bidder with the highest estimate, and that estimate is too high on average. The difference between the highest estimate and the average estimate is known as the winner’s curse correction. The size of the winner’s curse correction is larger the more bidders there are, but it tends to grow slowly beyond a dozen or so bidders.
If the bidders have the same information on a common value item, they will generally not earn profits on it. Indeed, there is a general principle that it is the privacy of information, rather than the accuracy of information, that leads to profits. Bidders earn profits on the information that they hold that is not available to others. Information held by others will be built into the bid price and therefore not lead to profits.
The U.S. Department of the Interior, when selling offshore oil leases, not only takes an up-front payment (the winning bid) but also takes one-sixth of the oil that is eventually pumped. Such a royalty scheme links the payment made to the outcome and, in a way, shares risk because the payment is higher when there is more oil. Similarly, a book contract provides an author with an upfront payment and a royalty. Many U.S. Department of Defense (DOD) purchases of major weapons systems involve cost-sharing, where the payments made pick up a portion of the cost. Purchases of ships, for example, generally involve 50%–70% cost sharing, which means the DOD pays a portion of cost overruns. The contract for U.S. television broadcast rights for the Summer Olympics in Seoul, South Korea, involved payments that depended on the size of the U.S. audience.
Royalties, cost-sharing, and contingent payments generally link the actual payment to the actual value, which is unknown at the time of the auction. Linkage shares risk, but linkage does something else, too. Linkage reduces the importance of estimates in the auction, replacing the estimates with actual values. That is, the price a bidder pays for an object, when fully linked to the true value, is just the true value. Thus, linkage reduces the importance of estimation in the auction by taking the price out of the bidder’s hands, at least partially.
The linkage principleThe expected price in an auction to sell rises the more the price is linked to the actual value.The linkage principle, and much of modern auction theory, was developed by Paul Milgrom (1948–). states that in auctions where bidders are buyers, the expected price rises the more the price is linked to the actual value. (In a parallel fashion, the expected price in an auction where bidders are selling falls.) Thus, linking price to value generally improves the performance of auctions. While this is a mathematically deep result, an extreme case is straightforward to understand. Suppose the government is purchasing by auction a contract for delivery of 10,000 gallons of gasoline each week for the next year. Suppliers face risk in the form of gasoline prices; if the government buys at a fixed price, the suppliers’ bids will build in a cushion to compensate for the risk and for the winner’s curse. In addition, because their estimates of future oil prices will generally vary, they will earn profits based on their private information about the value. In contrast, if the government buys only delivery and then pays for the cost of the gasoline, whatever it might be, any profits that the bidders earned based on their ability to estimate gasoline prices evaporate. The overall profit level of bidders falls, and the overall cost of the gasoline supply can fall. Of course, paying the cost of the gasoline reduces the incentive of the supplier to shop around for the best price, and that agency incentive effect must be balanced against the reduction in bidder profits from the auction to select a supplier.
We saw in Section 20.5 "The Winner’s Curse and Linkage" that the English auction tends to reduce regret relative to sealed-bid auctions and that the linkage principle suggests tying payments to value where possible. These are examples of auction design, in which auctions are designed to satisfy objectives of the auction designer. Proper auction design should match the rules of the auction to the circumstances of the bidders and the goal of the seller. Some of the principles of auction design include:
However, many of these principles change if the seller is facing a cartel. For example, it is easier for bidders to collude in a sealed-bid auction than in an English auction, and reserve prices should be made relatively high.
Reserve pricesMinimum bids in an auction. (minimum bids) have several effects. They tend to force marginal bidders to bid a bit higher, which increases the bids of all bidders and thus reduces bidder profits. However, reserve prices also lead to a failure to sell on occasion, and the optimal reserve trades off this failure to sell against the higher prices. In addition, reserve prices may reduce the incentive of bidders to investigate the sale, thus reducing participation, which is an additional negative consideration for a high reserve price.
Ascending price auctions like the English auction have several advantages. Such auctions reduce the complexity of the bidder’s problem because bidders can stretch their calculations out over time and because bidders can react to the behavior of others and not plan for every contingency in advance. In addition, because bidders in an English auction can see the behavior of others, there is a linkage created—the price paid by the winning bidder is influenced not just by that bidder’s information but also by the information held by others, tending to drive up the price, which is an advantage for the seller.
One caveat to the selection of the English auction is that risk aversion doesn’t affect the outcome in the private values case. In contrast, in a sealed-bid auction, risk aversion works to the advantage of the seller because bidders bid a little bit higher than they would have otherwise to reduce the risk of losing. Thus, in the private values case, risk-averse bidders will bid higher in the sealed-bid auction than in the English auction.
When considering the revelation of information, there is always an issue of lying and misleading. In the long run, lying and misleading are found out, and thus the standard approach is to ignore the possibility of lying. Making misleading statements is, in the long run, the same thing as silence because those who repeatedly lie or mislead are eventually discovered and then not believed. Thus, in the long run, a repeat seller has a choice of being truthful or silent. Because of the linkage principle, the policy of revealing truthful information about the value of the good for sale dominates the policy of concealing information because the revelation of information links the payment to the actual outcome.
In contrast, revealing information about the extent of competition may not increase the prices. Consider the case where occasionally there are three bidders, or the case where this is only one. If the extent of competition is concealed, bidders will bid without knowing the extent of competition. If the bidders are risk neutral, it turns out that the revelation doesn’t matter and the outcomes are the same on average. If, in contrast, bidders are risk averse, the concealment of information tends to increase the bid prices because the risk created by the uncertainty about the extent of competition works to the advantage of the seller. Of course, it may be difficult to conceal the extent of competition in the English auction, suggesting that a sealed-bid auction should be used instead.
Bidders with a large, known advantage have several deleterious effects. For example, incumbent telephone companies generally are willing to pay more for spectrum in their areas than outsiders are. Bidders bidding at an advantage discourage the participation of others because the others are likely to lose. This can result in a bidder with an advantage facing no competition and picking up the good cheaply. Second, rivals don’t present much competition to the advantaged bidder, even if the rivals do participate. Consequently, when a bidder has a large advantage over rivals, it is advantageous to handicap the advantaged bidder, thus favoring the rivals. This handicapping encourages participation and levels the playing field, forcing the advantaged bidder to bid more competitively to win.
A common means of favoring disadvantaged bidders is by the use of bidder creditsFavoritism in an auction for certain bidders in the form of discounts on payment.. For example, with a 20% bidder credit for disadvantaged bidders, a disadvantaged bidder has to pay only 80% of the face amount of the bid. This lets such a bidder bid 25% more (because a $100 payment corresponds to a $125 bid) than she would have otherwise, which makes the bidder a more formidable competitor. Generally, the ideal bidder credit is less than the actual advantage of the advantaged bidder.
Auction design is an exciting development in applied industrial organization, in which economic theory and experience is used to improve the performance of markets. The U.S. Federal Communications auctions of spectrum were the first major instance of auction design in an important practical setting, and the auction design was credited with increasing substantially the revenue raised by the government.
Some of the principles of auction design include: