Question: We have already learned that managers use differential analysis for make-or-buy decisions, product line decisions, and customer decisions. Differential analysis also provides a format that helps managers decide whether to accept special orders made by customers. What is a special order, and how can differential analysis be used to make a special order decision?
Answer: A special orderA unique one-time order made by a customer. is a unique one-time order made by a customer. Differential analysis provides a format that helps managers decide whether to accept or reject special orders, as shown in the example that follows.
Assume Tony’s T-shirts makes shirts for local soccer, baseball, basketball, and other sports teams. The owner, Tony, purchases the shirts and prints graphics on the shirts for each team. The graphics were designed several years ago, so design costs are no longer incurred. On average, Tony sells 1,000 shirts each month. Typical monthly financial data follow:
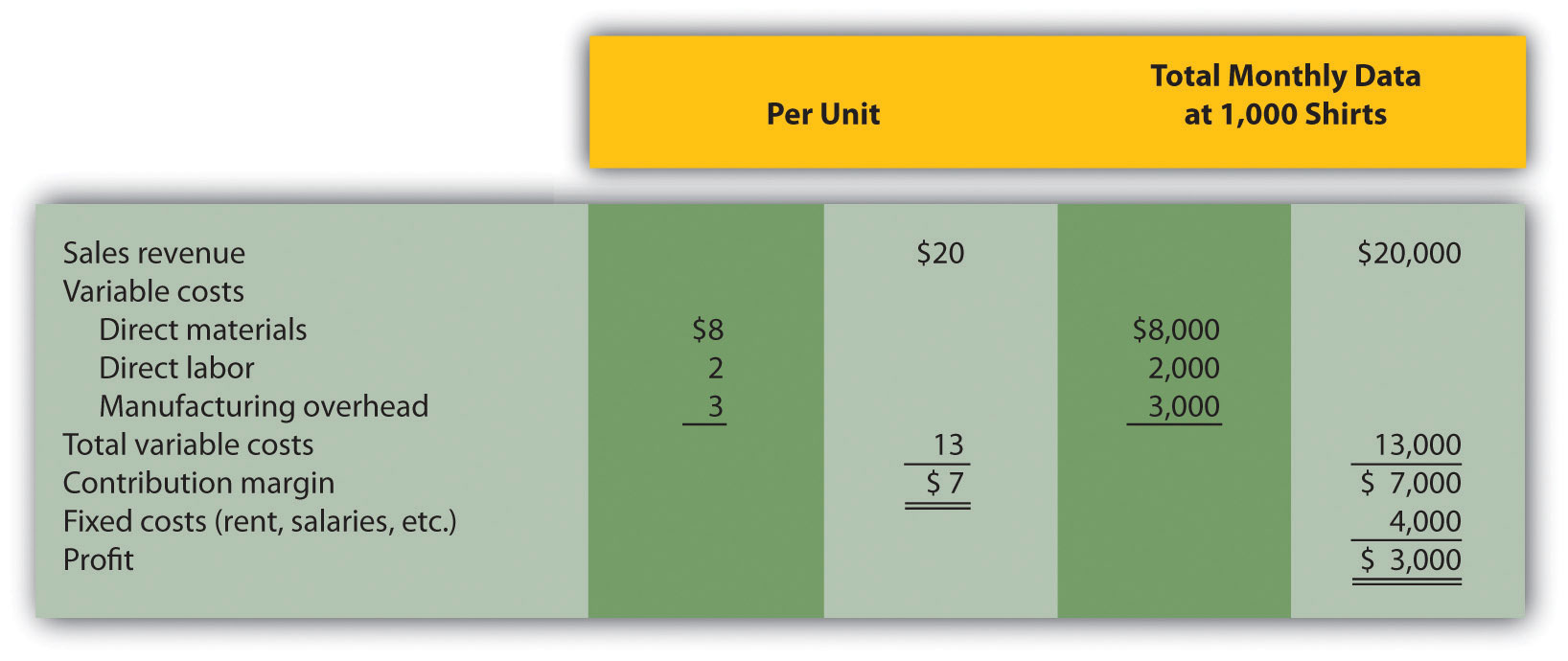
The monthly information provided relates to the company’s routine monthly operations. A representative of the local high school recently approached Tony to ask about a one-time special order. The high school will be hosting a statewide track and field event and is willing to pay Tony’s T-shirts $17 per shirt to make 200 custom T-shirts for the event. Because enough idle capacity exists to handle this order, it will not affect other sales. That is, Tony has the factory space and machinery available to produce more T-shirts.
Tony incurs the same variable costs of $13 per unit to produce the special order, and he will pay a firm $600 to design the graphics that will be printed on the shirts. This special order will have no other effect on Tony’s monthly fixed costs.
Question: Should Tony accept the special order?
Answer: Let’s use differential analysis to answer this question. As shown in Figure 7.13 "Special Order Differential Analysis for Tony’s T-Shirts", Alternative 1 assumes Tony rejects the special order, and Alternative 2 assumes he accepts the special order. The differential analysis in Figure 7.13 "Special Order Differential Analysis for Tony’s T-Shirts" shows that Tony’s would be better off accepting the special order, as profit increases $200.
Figure 7.13 Special Order Differential Analysis for Tony’s T-Shirts
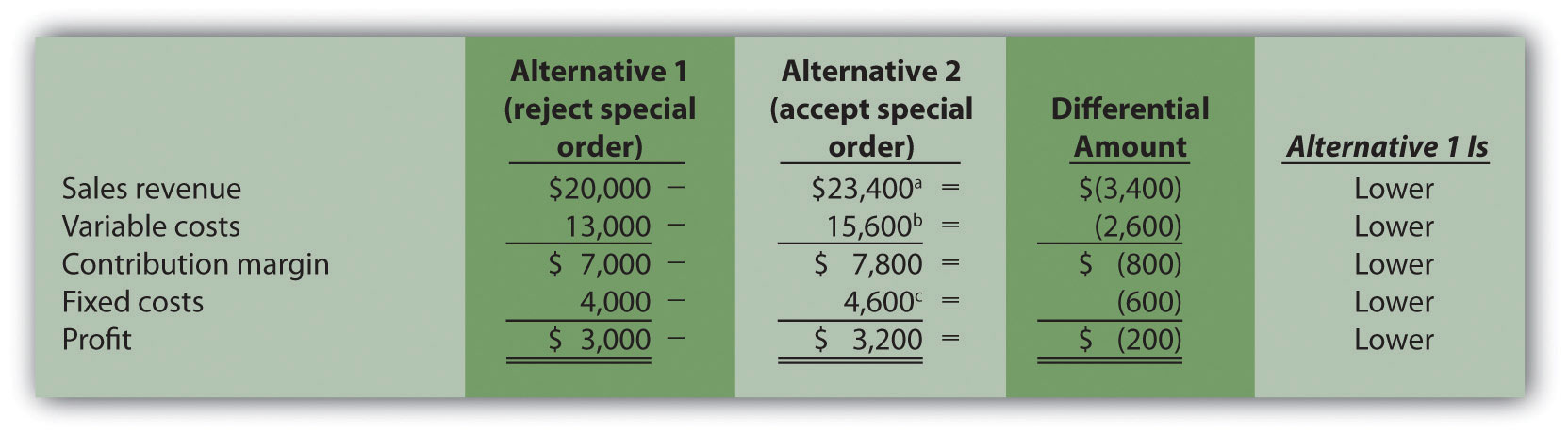
a $23,400 = $20,000 + ($17 per shirt × 200 shirts).
b $15,600 = $13,000 + ($13 × 200 shirts).
c $4,600 = $4,000 + $600 cost for special order design.
Figure 7.14 "Summary of Differential Analysis for Tony’s T-Shirts" provides an alternative presentation of differential analysis for Tony’s T-shirts. As discussed earlier in the chapter, this presentation summarizes the differential revenues and costs.
Figure 7.14 Summary of Differential Analysis for Tony’s T-Shirts

Note: Amounts shown in parentheses indicate a negative impact on profit, and amounts without parentheses indicate a positive impact on profit.
Figure 7.14 "Summary of Differential Analysis for Tony’s T-Shirts" shows the differential revenues and costs for the special order being considered. If Tony’s T-shirts accepts the special order, sales revenue will increase $3,400 with a corresponding increase in variable costs of $2,600. Fixed costs will increase by $600 because design work is required for the special order. Thus profit will increase by $200 (= $3,400 − $2,600 − $600).
Question: What assumptions were made with the differential analysis performed for Tony’s T-shirts?
Answer: We made two important assumptions in the Tony’s T-shirts special order example. The first assumption is that Tony’s has enough idle capacity to handle the order without disrupting regular customer orders. Suppose Tony’s T-shirts is operating at capacity and cannot produce any more T-shirts. Tony must turn away regular customers to make room for the special order. In this scenario, the opportunity cost of turning away existing customers must be considered in the differential analysis.
The second assumption is that this is a one-time order, and therefore represents a short-run pricing decision. If Tony’s T-shirts expects future orders from the high school at the $17 per shirt price, the company must consider the impact this might have on long-run pricing with other customers. That is, regular customers may hear of this special price and demand the same price, particularly those customers who have been loyal to Tony’s T-shirts for many years. Tony’s might be forced to lower prices for regular customers, thereby eroding the company’s profits over time. The key point is that companies evaluating special orders can drop prices in the short run to cover differential variable and fixed costs. But in the long run, prices must cover all variable and fixed costs.
Using Excel to Perform Differential Analysis
Managers often perform differential analysis with the help of computer software for several reasons:
An example of how to use Excel to perform differential analysis for the special order scenario presented in Figure 7.13 "Special Order Differential Analysis for Tony’s T-Shirts" is shown here. Although many accounting courses do not require the use of computer spreadsheets, you are encouraged to use spreadsheet software like Excel when preparing homework or working review problems.
The following monthly financial data are for Quicko’s, a company that makes photocopies for its customers. On average, Quicko’s makes 100,000 copies each month.

Quicko’s is approached by a local restaurant that would like to have 20,000 flyers copied. The restaurant asks Quicko’s to produce the flyers for 7 cents a copy rather than the standard price of 8 cents. Quicko’s can produce up to 130,000 copies a month, so the special order will not affect regular customer sales. Variable costs per copy will remain at 5 cents, but production of the restaurant flyers will require a special copy machine part that costs $250. This special order will have no other effect on monthly fixed costs.
Solution to Review Problem 7.6
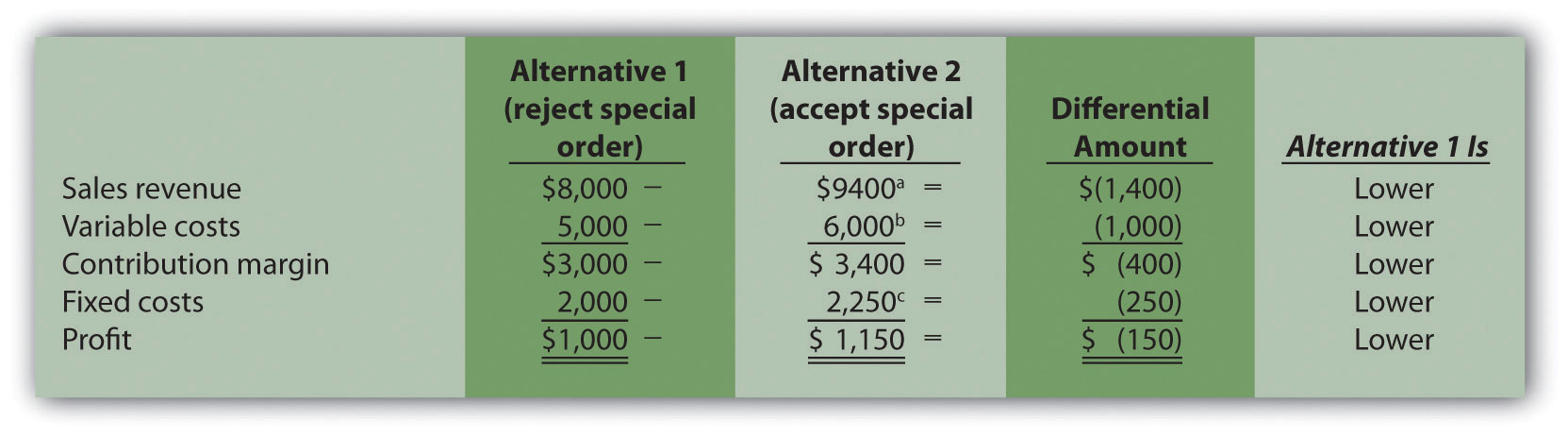
a $9,400 = $8,000 + ($0.07 per copy × 20,000 copies);or alternative approach: ($0.08 per copy × 100,000 copies) + ($0.07 per copy × 20,000 copies).
b $6,000 = $5,000 + ($0.05 per copy × 20,000 copies); or alternative approach: $0.05 × 120,000 copies.
c $2,250 = $2,000 + $250 cost for copy machine part.
This analysis shows that Quicko’s would be better off accepting the special order because profit is $150 higher for Alternative 2.

Note: Amounts shown in parentheses indicate a negative impact on profit, and amounts without parentheses indicate a positive impact on profit.
Assuming Quicko’s has a capacity of 100,000 copies per month, the analysis shows the company would be better off rejecting the special order because profit is $450 higher for this alternative.
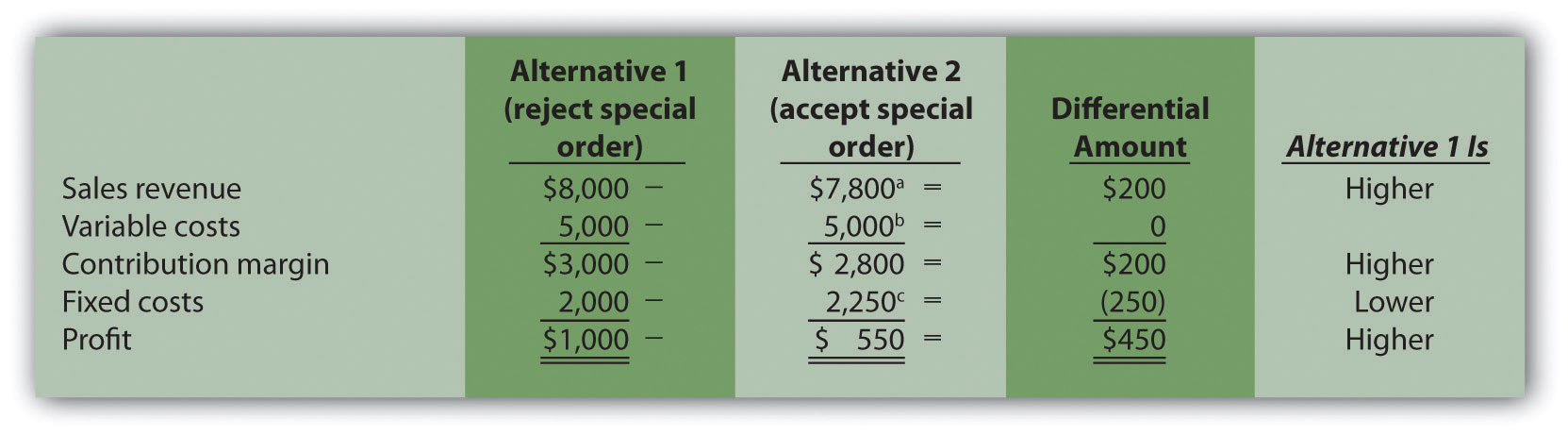
a $7,800 = ($0.08 × 80,000 regular customer copies) + ($0.07 × 20,000 special order copies).
b $2,250 = $2,000 + $250 cost for copy machine part.