There’s a New Yorker cartoon that pretty accurately portrays life for a field researcher (Cotham, 2003).Cotham, F. (2003, September 1). Two barbarians and a professor of barbarian studies. The New Yorker. Retrieved from http://www.cartoonbank.com/2003/two-barbarians-and-a-professor-of-barbarian-studies/invt/126562 It depicts “Two Barbarians and a Professor of Barbarian Studies.” As field researchers, just as in the cartoon, we immerse ourselves in the settings that we study. While the extent to which we immerse ourselves varies (note in the cartoon the professor is riding a horse but has chosen to retain his professorial jacket and pipe), what all field researchers have in common is their participation in “the field.”
Field researchA qualitative method of data collection that involves observing, interacting with, and interviewing people in their natural settings. is a qualitative method of data collection aimed at understanding, observing, and interacting with people in their natural settings. Thus when social scientists talk about being in “the field,” they’re talking about being out in the real world and involved in the everyday lives of the people they are studying. Sometimes researchers use the terms ethnography or participant observation to refer to this method of data collection; the former is most commonly used in anthropology, while the latter is used commonly in sociology. In this text, we’ll use two main terms: field research and participant observation. You might think of field research as an umbrella term that includes the myriad activities that field researchers engage in when they collect data: they participate, they observe, they usually interview some of the people they observe, and they typically analyze documents or artifacts created by the people they observe.
Figure 10.2
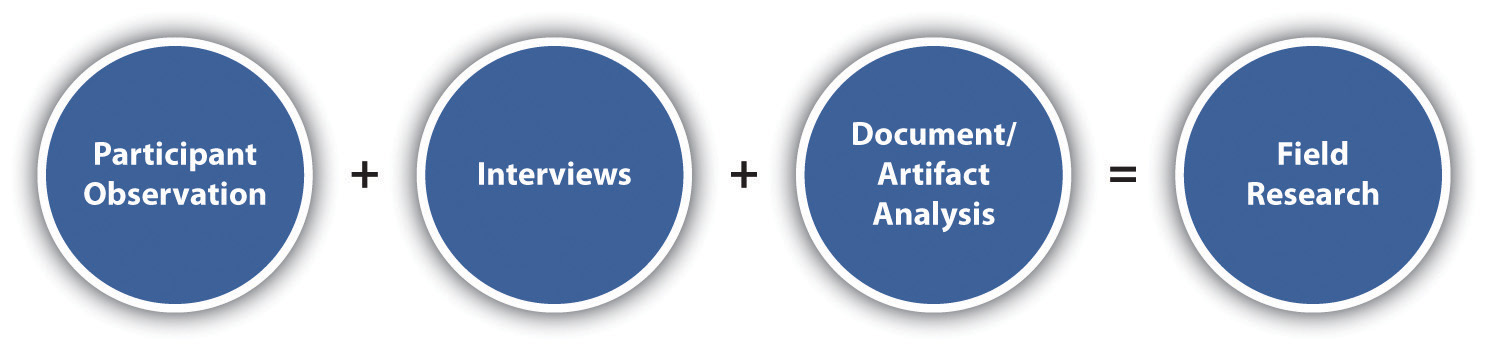
Field research typically involves a combination of participant observation, interviewing, and document or artifact analysis. This chapter focuses primarily on participant observation.
Because we cover interviews and document/artifact analysis in Chapter 9 "Interviews: Qualitative and Quantitative Approaches" and Chapter 11 "Unobtrusive Research: Qualitative and Quantitative Approaches", here we’ll focus only on the participation and observation aspects of field research. These aspects of field research are usually referenced together and are known as participant observationThe parts of field research that involve spending time with and watching one’s research participants; interviewing and document/artifact analysis are the other two components of field research.. Like field research, participant observation also has multiple meanings. Researchers conducting participant observation vary in the extent to which they participate or observe (Junker, 1960).Junker, B. H. (1960). Field work: An introduction to the social sciences. Chicago, IL: University of Chicago Press. You might say that there’s a continuum of participant observation, where complete observation lies at end of the continuum and complete participation lies at the other end.
In other chapters, we discuss two works that could fall on either end of the participant observation continuum. Barrie Thorne’s (1993)Thorne, B. (1993). Gender play: Girls and boys in school. New Brunswick, NJ: Rutgers University Press. observations of children in classrooms, school cafeterias, hallways, and playgrounds rest near the complete observation end of the continuum. Rather than actually pretending to be an elementary school student and interacting with her research participants as they would each other, Thorne observed (which, as discussed in Chapter 4 "Beginning a Research Project", was probably a wise move since it would have been difficult to convince the students that she was one of them). Laud Humphreys’s (1970)Humphreys, L. (1970). Tearoom trade: Impersonal sex in public places. London, UK: Duckworth. research on the tearoom trade, described in Chapter 3 "Research Ethics", could be said to rest on the other end of the continuum. Rather than only observe, Humphreys played the key tearoom role of watch queen, a role that nonresearcher participants in the trade also played. Humphreys also did not tell many of the people he observed that he was a researcher; thus from the perspectives of many of his “subjects,” he was only a participant. The participant observation continuum is represented in Figure 10.3.
There are pros and cons associated with both aspects of the participant observer’s role. Complete observers may miss important aspects of group interaction and don’t have the opportunity to fully grasp what life is like for the people they observe. At the same time, sitting back and observing may grant them opportunities to see interactions that they would miss were they more involved. Complete participation has the benefit of allowing researchers a real taste of life in the group that they study. Some argue that participation is the only way to understand what it is that we investigate. On the other hand, complete participants may find themselves in situations that they’d rather not face but cannot excuse themselves from because they’ve adopted the role of complete participant. Also, complete participants who do not reveal themselves as researchers must face the ethical quandary of possibly deceiving their “subjects.” In reality, most field research projects lie somewhere near the middle of the observer-participant continuum. Field researchers typically participate to at least some extent in their field sites, but there are also times when they may just observe. Where would you feel most comfortable as a field researcher—as an observer, a participant, or a bit of both?
As you might have imagined based on the examples of Thorne’s and Humphreys’s work, field research is well equipped to answer “how” kinds of questions. Whereas survey researchers often aim to answer “why” questions, field researchers ask how the processes they study occur, how the people they spend time with in the field interact, and how events unfold. Table 10.1 "Field Research Examples" presents just a few examples of the kinds of questions field researchers have asked in past projects along with a brief summary of where and what role those researchers took in the field. The examples presented in Table 10.1 "Field Research Examples" by no means represent an exhaustive list of the variations of questions field researchers have asked or of the range of field research projects that have been conducted over the years, but they do provide a snapshot of the kinds of work sociological field researchers engage in.
Table 10.1 Field Research Examples
| Question | Researcher role | Author (year) |
|---|---|---|
| How is the social structure of a local “slum” organized? | Over 3 years of participation and observations among an Italian community in Boston’s North End | Whyte (1942)William Foote Whyte is considered by many to be the pioneer of the use of participant observation methods in sociological studies. Whyte, W. F. (1942). Street corner society: The social structure of an Italian slum. Chicago, IL: University of Chicago Press. |
| How do the urban poor live? | Twenty months of participation and observations among an African American community in Washington, DC | Liebow (1967)Liebow, E. (1967). Tally’s corner: A study of Negro streetcorner men. Boston, MA: Little, Brown. |
| Why and how do workers consent to their own exploitation? | Ten months of participation as a machine operator in a Chicago factory along with observations of workers in the factory | Burawoy (1979)Burawoy, M. (1979). Manufacturing consent: Changes in the labor process under monopoly capitalism. Chicago, IL: University of Chicago Press. |
| How is erotic labor organized in two different countries, and what are sex workers’ experiences in each? | Brief participation in sex transactions in the Netherlands and California along with observations of and interviews with sex workers in both locations | Chapkis (1997)Chapkis, W. (1997). Live sex acts: Women performing erotic labor. New York, NY: Routledge. |
| How does childrearing differ across social classes? | Approximately one month each participating and observing in the homes and lives of 12 different families | Lareau (2003)Lareau, A. (2003). Unequal childhoods: Class, race, and family life. Berkeley: University of California Press. |
| How is masculinity constructed by and among high school students, and what does this mean for our understandings of gender and sexuality? | Eighteen months of observations and interviews in a racially diverse working-class high school | Pascoe (2007)Pascoe, C. J. (2007). Dude, you’re a fag: Masculinity and sexuality in high school. Berkeley: University of California Press. |
| How do sports play a role in shaping gender, class, family, and community? | Participation as a youth soccer volunteer along with observations and interviews | Messner (2009)Messner, M. (2009). It’s all for the kids: Gender, families, and youth sports. Berkeley: University of California Press. |
Field research is a method that was originally crafted by anthropologists for the purpose of cultural understanding and interpretation (Wolcott, 2008).Wolcott, H. F. (2008). Ethnography: A way of seeing (2nd ed.). Lanham, MD: Altamira Press. Dissatisfied with studying groups of people based solely on secondhand accounts and inspection of artifacts, several anthropologists decided to try living in or near the communities they studied to learn from and about them. Two anthropologists in particular, Franz Boas (1888)Boas, F. (1888). The central Eskimo. Washington, DC: Bureau of American Ethnology. and Bronislaw Malinowski (1922),Malinowski, B. (1922). Argonauts of the western Pacific: An account of native enterprise and adventure in the archipelagoes of Melanesian New Guinea. London, UK: G. Routledge & Sons; New York, NY: E. P. Dutton. are credited with developing this method around the turn of the 20th century. Boas lived with native populations in Canada and in the American Northwest. Malinowski lived in Papua New Guinea with people who were native to the area. Sociologists picked up on the idea and on the benefits of field research (which we’ll examine in Section 10.2 "Pros and Cons of Field Research"). Soon a number of sociologists had embraced this new method and adapted field research for their own studies of groups. Many of the early field researchers in sociology were former social workers who got interested in sociological research because of experiences in their roles as social reformers. The University of Chicago in particular played a key role in the development of American field research through, among other projects, its involvement in Hull House,Jane Addams Hull House Association. Retrieved from http://www.hullhouse.org a social settlement founded for European immigrants in Chicago (Deegan, 1986).Deegan, M. J. (1986). Jane Addams and the men of the Chicago School, 1892–1918. New Brunswick, NJ: Transaction Books.