Scientists discovered much of what we know about the structure of the atom by observing the interaction of atoms with various forms of radiant, or transmitted, energy, such as the energy associated with the visible light we detect with our eyes, the infrared radiation we feel as heat, the ultraviolet light that causes sunburn, and the x-rays that produce images of our teeth or bones. All these forms of radiant energy should be familiar to you. We begin our discussion of the development of our current atomic model by describing the properties of waves and the various forms of electromagnetic radiation.
Figure 6.1 A Wave in Water

When a drop of water falls onto a smooth water surface, it generates a set of waves that travel outward in a circular direction.
A waveA periodic oscillation that transmits energy through space. is a periodic oscillation that transmits energy through space. Anyone who has visited a beach or dropped a stone into a puddle has observed waves traveling through water (Figure 6.1 "A Wave in Water"). These waves are produced when wind, a stone, or some other disturbance, such as a passing boat, transfers energy to the water, causing the surface to oscillate up and down as the energy travels outward from its point of origin. As a wave passes a particular point on the surface of the water, anything floating there moves up and down.
Figure 6.2 Important Properties of Waves
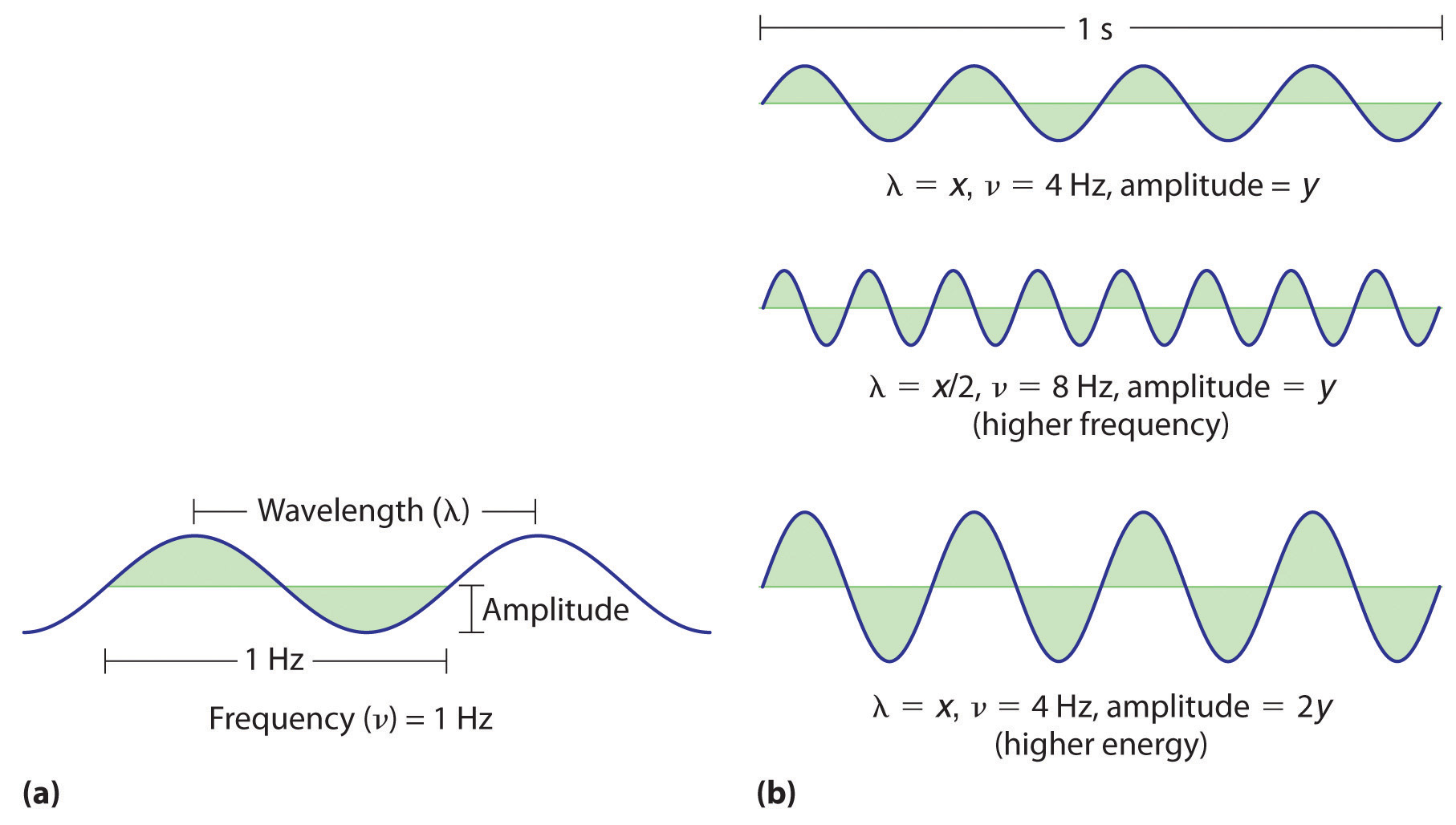
(a) Wavelength (λ), frequency (ν, labeled in Hz), and amplitude are indicated on this drawing of a wave. (b) The wave with the shortest wavelength has the greatest number of wavelengths per unit time (i.e., the highest frequency). If two waves have the same frequency and speed, the one with the greater amplitude has the higher energy.
Waves have characteristic properties (Figure 6.2 "Important Properties of Waves"). As you may have noticed in Figure 6.1 "A Wave in Water", waves are periodicPhenomena, such as waves, that repeat regularly in both space and time.; that is, they repeat regularly in both space and time. The distance between two corresponding points in a wave—between the midpoints of two peaks, for example, or two troughs—is the wavelength (λ)The distance between two corresponding points in a wave—between the midpoints of two peaks or two troughs..λ is the lowercase Greek lambda, and ν is the lowercase Greek nu. Wavelengths are described by a unit of distance, typically meters. The frequency (ν)The number of oscillations (i.e., of a wave) that pass a particular point in a given period of time. of a wave is the number of oscillations that pass a particular point in a given period of time. The usual units are oscillations per second (1/s = s−1), which in the SI system is called the hertz (Hz).Named after German physicist Heinrich Hertz (1857–1894), a pioneer in the field of electromagnetic radiation. The amplitudeThe vertical height of a wave, which is defined as half the peak-to-trough height., or vertical height, of a wave is defined as half the peak-to-trough height; as the amplitude of a wave with a given frequency increases, so does its energy. As you can see in Figure 6.2 "Important Properties of Waves", two waves can have the same amplitude but different wavelengths and vice versa. The distance traveled by a wave per unit time is its speed (v)The distance traveled by a wave per unit time., which is typically measured in meters per second (m/s). The speed of a wave is equal to the product of its wavelength and frequency:
Equation 6.1
Water waves are slow compared to sound waves, which can travel through solids, liquids, and gases. Whereas water waves may travel a few meters per second, the speed of sound in dry air at 20°C is 343.5 m/s. Ultrasonic waves, which travel at an even higher speed (>1500 m/s) and have a greater frequency, are used in such diverse applications as locating underwater objects and the medical imaging of internal organs.
Water waves transmit energy through space by the periodic oscillation of matter (the water). In contrast, energy that is transmitted, or radiated, through space in the form of periodic oscillations of electric and magnetic fields is known as electromagnetic radiationEnergy that is transmitted, or radiated, through space in the form of periodic oscillations of electric and magnetic fields. (Figure 6.3 "The Nature of Electromagnetic Radiation"). Some forms of electromagnetic radiation are shown in Figure 6.4 "The Electromagnetic Spectrum". In a vacuum, all forms of electromagnetic radiation—whether microwaves, visible light, or gamma rays—travel at the speed of light (c)The speed with which all forms of electromagnetic radiation travel in a vacuum., a fundamental physical constant with a value of 2.99792458 × 108 m/s (which is about 3.00 ×108 m/s or 1.86 × 105 mi/s). This is about a million times faster than the speed of sound.
Figure 6.3 The Nature of Electromagnetic Radiation
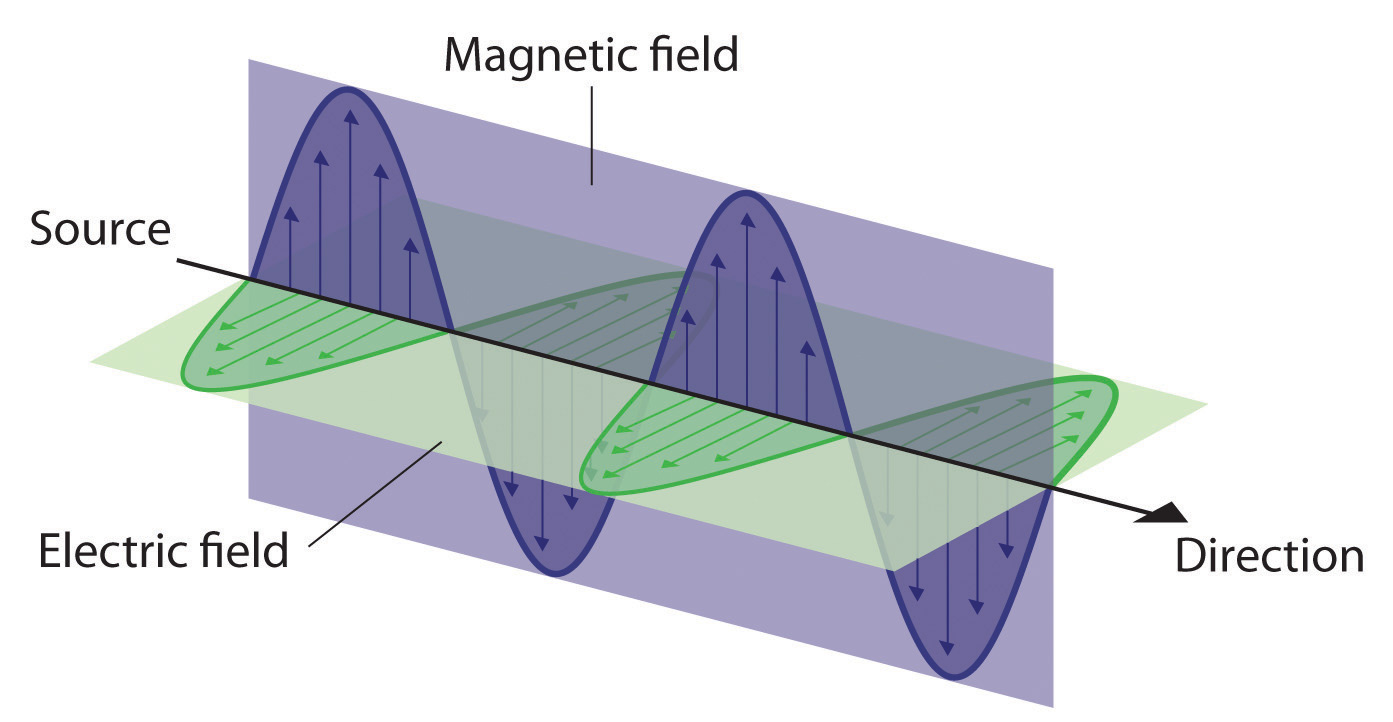
All forms of electromagnetic radiation consist of perpendicular oscillating electric and magnetic fields.
Because the various kinds of electromagnetic radiation all have the same speed (c), they differ in only wavelength and frequency. As shown in Figure 6.4 "The Electromagnetic Spectrum" and Table 6.1 "Common Wavelength Units for Electromagnetic Radiation", the wavelengths of familiar electromagnetic radiation range from 101 m for radio waves to 10−12 m for gamma rays, which are emitted by nuclear reactions. By replacing v with c in Equation 6.1, we can show that the frequency of electromagnetic radiation is inversely proportional to its wavelength:
Equation 6.2
For example, the frequency of radio waves is about 108 Hz, whereas the frequency of gamma rays is about 1020 Hz. Visible light, which is electromagnetic radiation that can be detected by the human eye, has wavelengths between about 7 × 10−7 m (700 nm, or 4.3 × 1014 Hz) and 4 × 10−7 m (400 nm, or 7.5 × 1014 Hz). Within this range, the eye perceives radiation of different wavelengths (or frequencies) as light of different colors, ranging from red to violet in order of decreasing wavelength. The components of white light—a mixture of all the frequencies of visible light—can be separated by a prism, as shown in part (b) in Figure 6.4 "The Electromagnetic Spectrum". A similar phenomenon creates a rainbow, where water droplets suspended in the air act as tiny prisms.
Figure 6.4 The Electromagnetic Spectrum
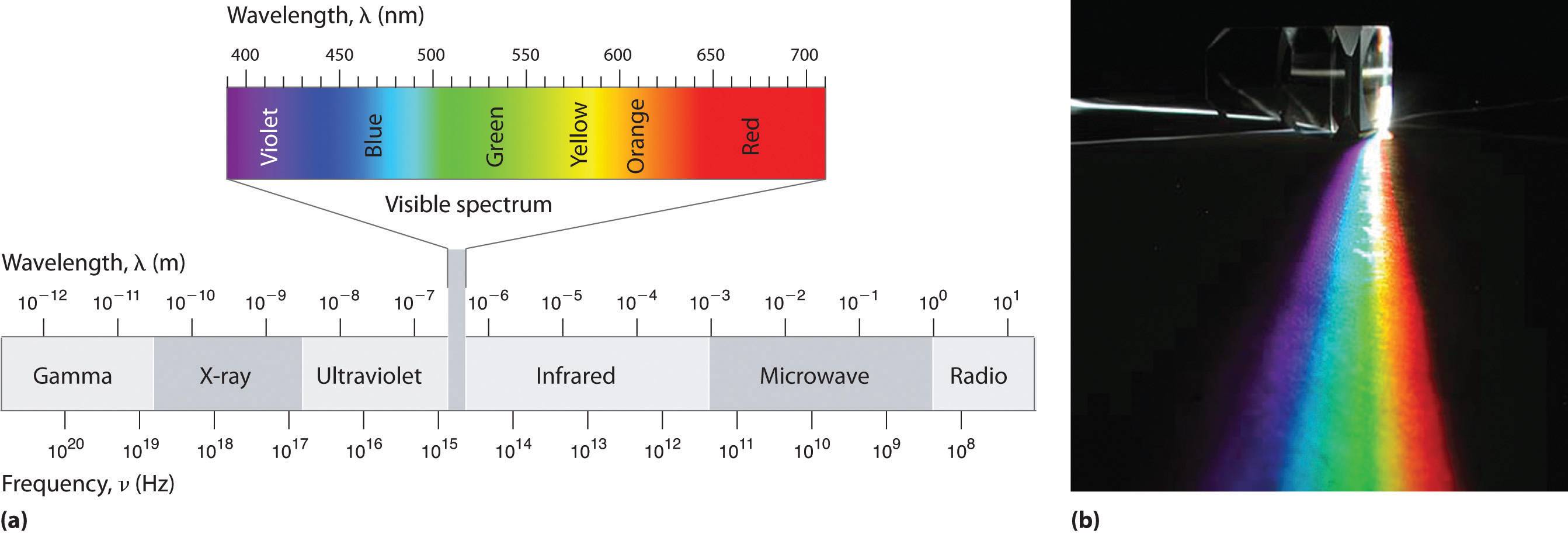
(a) This diagram shows the wavelength and frequency ranges of electromagnetic radiation. The visible portion of the electromagnetic spectrum is the narrow region with wavelengths between about 400 and 700 nm. (b) When white light is passed through a prism, it is split into light of different wavelengths, whose colors correspond to the visible spectrum.
Table 6.1 Common Wavelength Units for Electromagnetic Radiation
| Unit | Symbol | Wavelength (m) | Type of Radiation |
|---|---|---|---|
| picometer | pm | 10−12 | gamma ray |
| angstrom | Å | 10−10 | x-ray |
| nanometer | nm | 10−9 | x-ray |
| micrometer | μm | 10−6 | infrared |
| millimeter | mm | 10−3 | infrared |
| centimeter | cm | 10−2 | microwave |
| meter | m | 100 | radio |
As you will soon see, the energy of electromagnetic radiation is directly proportional to its frequency and inversely proportional to its wavelength:
Equation 6.3
Equation 6.4
Whereas visible light is essentially harmless to our skin, ultraviolet light, with wavelengths of ≤ 400 nm, has enough energy to cause severe damage to our skin in the form of sunburn. Because the ozone layer described in Chapter 3 "Chemical Reactions" absorbs sunlight with wavelengths less than 350 nm, it protects us from the damaging effects of highly energetic ultraviolet radiation.
The energy of electromagnetic radiation increases with increasing frequency and decreasing wavelength.
Your favorite FM radio station, WXYZ, broadcasts at a frequency of 101.1 MHz. What is the wavelength of this radiation?
Given: frequency
Asked for: wavelength
Strategy:
Substitute the value for the speed of light in meters per second into Equation 6.2 to calculate the wavelength in meters.
Solution:
From Equation 6.2, we know that the product of the wavelength and the frequency is the speed of the wave, which for electromagnetic radiation is 2.998 × 108 m/s:
λν = c = 2.998 × 108 m/sThus the wavelength λ is given by
Exercise
As the police officer was writing up your speeding ticket, she mentioned that she was using a state-of-the-art radar gun operating at 35.5 GHz. What is the wavelength of the radiation emitted by the radar gun?
Answer: 8.45 mm
In Section 6.2 "The Quantization of Energy" and Section 6.3 "Atomic Spectra and Models of the Atom", we describe how scientists developed our current understanding of the structure of atoms using the scientific method described in Chapter 1 "Introduction to Chemistry". You will discover why scientists had to rethink their classical understanding of the nature of electromagnetic energy, which clearly distinguished between the particulate behavior of matter and the wavelike nature of energy.
relationship between wavelength, frequency, and speed of a wave
Equation 6.1: λν = v
relationship between wavelength, frequency, and speed of electromagnetic radiation
Equation 6.2: c = λν
A basic knowledge of the electronic structure of atoms requires an understanding of the properties of waves and electromagnetic radiation. A wave is a periodic oscillation by which energy is transmitted through space. All waves are periodic, repeating regularly in both space and time. Waves are characterized by several interrelated properties: wavelength (λ), the distance between successive waves; frequency (ν), the number of waves that pass a fixed point per unit time; speed (v), the rate at which the wave propagates through space; and amplitude, the magnitude of the oscillation about the mean position. The speed of a wave is equal to the product of its wavelength and frequency. Electromagnetic radiation consists of two perpendicular waves, one electric and one magnetic, propagating at the speed of light (c). Electromagnetic radiation is radiant energy that includes radio waves, microwaves, visible light, x-rays, and gamma rays, which differ only in their frequencies and wavelengths.
What are the characteristics of a wave? What is the relationship between electromagnetic radiation and wave energy?
At constant wavelength, what effect does increasing the frequency of a wave have on its speed? its amplitude?
List the following forms of electromagnetic radiation in order of increasing wavelength: x-rays, radio waves, infrared waves, microwaves, ultraviolet waves, visible waves, and gamma rays. List them in order of increasing frequency. Which has the highest energy?
A large industry is centered on developing skin-care products, such as suntan lotions and cosmetics, that cannot be penetrated by ultraviolet radiation. How does the wavelength of visible light compare with the wavelength of ultraviolet light? How does the energy of visible light compare with the energy of ultraviolet light? Why is this industry focused on blocking ultraviolet light rather than visible light?
The human eye is sensitive to what fraction of the electromagnetic spectrum, assuming a typical spectral range of 104 to 1020 Hz? If we came from the planet Krypton and had x-ray vision (i.e., if our eyes were sensitive to x-rays in addition to visible light), how would this fraction be changed?
What is the frequency in megahertz corresponding to each wavelength?
What is the frequency in megahertz corresponding to each wavelength?
Line spectra are also observed for molecular species. Given the following characteristic wavelengths for each species, identify the spectral region (ultraviolet, visible, etc.) in which the following line spectra will occur. Given 1.00 mol of each compound and the wavelength of absorbed or emitted light, how much energy does this correspond to?
What is the speed of a wave in meters per second that has a wavelength of 1250 m and a frequency of 2.36 × 105 s−1?
A wave travels at 3.70 m/s with a frequency of 4.599 × 107 Hz and an amplitude of 1.0 m. What is its wavelength in nanometers?
An AM radio station broadcasts with a wavelength of 248.0 m. What is the broadcast frequency of the station in kilohertz? An AM station has a broadcast range of 92.6 MHz. What is the corresponding wavelength range in meters for this reception?
An FM radio station broadcasts with a wavelength of 3.21 m. What is the broadcast frequency of the station in megahertz? An FM radio typically has a broadcast range of 82–112 MHz. What is the corresponding wavelength range in meters for this reception?
A microwave oven operates at a frequency of approximately 2450 MHz. What is the corresponding wavelength? Water, with its polar molecules, absorbs electromagnetic radiation primarily in the infrared portion of the spectrum. Given this fact, why are microwave ovens used for cooking food?