Many vital chemical and physical processes take place exclusively in aqueous solution, including the complex biochemical reactions that occur in living organisms and the reactions that rust and corrode steel objects, such as bridges, ships, and automobiles. Among the most important reactions in aqueous solution are those that can be categorized as acid–base, precipitation, and complexation reactions. So far, our discussions of these reactions have been largely qualitative. In this chapter and Chapter 17 "Solubility and Complexation Equilibriums", however, we take a more quantitative approach to understanding such reactions, using the concept of chemical equilibrium that we developed in Chapter 15 "Chemical Equilibrium" for simple gas-phase reactions. We will begin by revisiting acid–base reactions in a qualitative fashion and then develop quantitative methods to describe acid–base equilibriums. In Chapter 17 "Solubility and Complexation Equilibriums", we will use the same approach to describe the equilibriums involved in the dissolution of sparingly soluble solids and the formation of metal complexes.

Indicators are used to monitor changes in pH. The pH of a solution can be monitored using an acid–base indicator, a substance that undergoes a color change within a specific pH range that is characteristic of that indicator. The color changes for seven commonly used indicators over a pH range of 1–10 are shown here.
In Chapter 4 "Reactions in Aqueous Solution", we described how acid rain can adversely affect the survival of marine life and plant growth. Many significant phenomena, such as acid rain, can be understood only in terms of the acid–base behavior of chemical species. As we expand our discussion of acid–base behavior in this chapter, you will learn why lemon slices are served with fish, why the strengths of acids and bases can vary over many orders of magnitude, and why rhubarb leaves are toxic to humans. You will also understand how the pH of your blood is kept constant, even though you produce large amounts of acid when you exercise.
As you learned in Chapter 4 "Reactions in Aqueous Solution" and Chapter 8 "Ionic versus Covalent Bonding", acids and bases can be defined in several different ways (Table 16.1 "Definitions of Acids and Bases"). Recall that the Arrhenius definition of an acid is a substance that dissociates in water to produce H+ ions (protons), and an Arrhenius base is a substance that dissociates in water to produce OH− (hydroxide) ions. According to this view, an acid–base reaction involves the reaction of a proton with a hydroxide ion to form water. Although Brønsted and Lowry defined an acid similarly to Arrhenius by describing an acid as any substance that can donate a proton, the Brønsted–Lowry definition of a base is much more general than the Arrhenius definition. In Brønsted–Lowry terms, a base is any substance that can accept a proton, so a base is not limited to just a hydroxide ion. This means that for every Brønsted–Lowry acid, there exists a corresponding conjugate base with one fewer proton, as we demonstrated in Chapter 4 "Reactions in Aqueous Solution". Consequently, all Brønsted–Lowry acid–base reactions actually involve two conjugate acid–base pairs and the transfer of a proton from one substance (the acid) to another (the base). In contrast, the Lewis definition of acids and bases, discussed in Chapter 8 "Ionic versus Covalent Bonding", focuses on accepting or donating pairs of electrons rather than protons. A Lewis base is an electron-pair donor, and a Lewis acid is an electron-pair acceptor.
Table 16.1 Definitions of Acids and Bases
| Acids | Bases | |
|---|---|---|
| Arrhenius | H+ donor | OH− donor |
| Brønsted–Lowry | H+ donor | H+ acceptor |
| Lewis | electron-pair acceptor | electron-pair donor |
Because this chapter deals with acid–base equilibriums in aqueous solution, our discussion will use primarily the Brønsted–Lowry definitions and nomenclature. Remember, however, that all three definitions are just different ways of looking at the same kind of reaction: a proton is an acid, and the hydroxide ion is a base—no matter which definition you use. In practice, chemists tend to use whichever definition is most helpful to make a particular point or understand a given system. If, for example, we refer to a base as having one or more lone pairs of electrons that can accept a proton, we are simply combining the Lewis and Brønsted–Lowry definitions to emphasize the characteristic properties of a base.
In Chapter 4 "Reactions in Aqueous Solution", we also introduced the acid–base properties of water, its autoionization reaction, and the definition of pH. The purpose of this section is to review those concepts and describe them using the concepts of chemical equilibrium developed in Chapter 15 "Chemical Equilibrium".
The structure of the water molecule, with its polar O–H bonds and two lone pairs of electrons on the oxygen atom, was described in Chapter 4 "Reactions in Aqueous Solution" and Chapter 8 "Ionic versus Covalent Bonding", and the structure of liquid water was discussed in Chapter 13 "Solutions". Recall that because of its highly polar structure, liquid water can act as either an acid (by donating a proton to a base) or a base (by using a lone pair of electrons to accept a proton). For example, when a strong acid such as HCl dissolves in water, it dissociates into chloride ions (Cl−) and protons (H+). As you learned in Chapter 4 "Reactions in Aqueous Solution", the proton, in turn, reacts with a water molecule to form the hydronium ion (H3O+):
Equation 16.1
In this reaction, HCl is the acid, and water acts as a base by accepting an H+ ion. The reaction in Equation 16.1 is often written in a simpler form by removing H2O from each side:
Equation 16.2
HCl(aq) → H+(aq) + Cl−(aq)In Equation 16.2, the hydronium ion is represented by H+, although free H+ ions do not exist in liquid water.
Water can also act as an acid, as shown in Equation 16.3. In this equilibrium reaction, H2O donates a proton to NH3, which acts as a base:
Equation 16.3
Thus water is amphiproticSubstances that can behave as either an acid or a base in a chemical reaction, depending on the nature of the other reactant(s)., meaning that it can behave as either an acid or a base, depending on the nature of the other reactant. Notice that Equation 16.3 is an equilibrium reaction as indicated by the double arrow.
Because water is amphiprotic, one water molecule can react with another to form an OH− ion and an H3O+ ion in an autoionization process:
Equation 16.4
The equilibrium constant K for this reaction can be written as follows:
Equation 16.5
When pure liquid water is in equilibrium with hydronium and hydroxide ions at 25°C, the concentrations of the hydronium ion and the hydroxide ion are equal: [H3O+] = [OH−] = 1.003 × 10−7 M. Thus the number of dissociated water molecules is very small indeed, approximately 2 ppb. We can calculate [H2O] at 25°C from the density of water at this temperature (0.997 g/mL):
Equation 16.6
With so few water molecules dissociated, the equilibrium of the autoionization reaction (Equation 16.4) lies far to the left. Consequently, [H2O] is essentially unchanged by the autoionization reaction and can be treated as a constant. Incorporating this constant into the equilibrium expression allows us to rearrange Equation 16.5 to define a new equilibrium constant, the ion-product constant of liquid water (Kw)An equilibrium constant for the autoionization of water, ⇌ + in which the concentration of water is treated as a constant: = = :
Equation 16.7
Substituting the values for [H3O+] and [OH−] at 25°C into this expression,
Equation 16.8
Thus, to three significant figures, Kw = 1.01 × 10−14 M. Like any other equilibrium constant, Kw varies with temperature, ranging from 1.15 × 10−15 at 0°C to 4.99 × 10−13 at 100°C.
In pure water, the concentrations of the hydronium ion and the hydroxide ion are equal, and the solution is therefore neutral. If [H3O+] > [OH−], however, the solution is acidic, whereas if [H3O+] < [OH−], the solution is basic. For an aqueous solution, the H3O+ concentration is a quantitative measure of acidity: the higher the H3O+ concentration, the more acidic the solution. Conversely, the higher the OH− concentration, the more basic the solution. In most situations that you will encounter, the H3O+ and OH− concentrations from the dissociation of water are so small (1.003 × 10−7 M) that they can be ignored in calculating the H3O+ or OH− concentrations of solutions of acids and bases, but this is not always the case.
The pH scale is a concise way of describing the H3O+ concentration and hence the acidity or basicity of a solution. Recall from Chapter 4 "Reactions in Aqueous Solution" that pH and the H+ (H3O+) concentration are related as follows:
Equation 16.9
Equation 16.10
Because the scale is logarithmic, a pH difference of 1 between two solutions corresponds to a difference of a factor of 10 in their hydronium ion concentrations. (Refer to Essential Skills 3 in Chapter 4 "Reactions in Aqueous Solution", Section 4.10 "Essential Skills 3", if you need to refresh your memory about how to use logarithms.) Recall also that the pH of a neutral solution is 7.00 ([H3O+] = 1.0 × 10−7 M), whereas acidic solutions have pH < 7.00 (corresponding to [H3O+] > 1.0 × 10−7) and basic solutions have pH > 7.00 (corresponding to [H3O+] < 1.0 × 10−7).
Similar notation systems are used to describe many other chemical quantities that contain a large negative exponent. For example, chemists use an analogous pOH scale to describe the hydroxide ion concentration of a solution. The pOH and [OH−] are related as follows:
Equation 16.11
Equation 16.12
The constant Kw can also be expressed using this notation, where pKw = −log Kw.
Because a neutral solution has [OH−] = 1.0 × 10−7, the pOH of a neutral solution is 7.00. Consequently, the sum of the pH and the pOH for a neutral solution at 25°C is 7.00 + 7.00 = 14.00. We can show that the sum of pH and pOH is equal to 14.00 for any aqueous solution at 25°C by taking the negative logarithm of both sides of Equation 16.7:
Equation 16.13
Thus at any temperature, pH + pOH = pKw, so at 25°C, where Kw = 1.0 × 10−14, pH + pOH = 14.00. More generally, the pH of any neutral solution is half of the pKw at that temperature. The relationship among pH, pOH, and the acidity or basicity of a solution is summarized graphically in Figure 16.1 "The Inverse Relationship between the pH and pOH Scales" over the common pH range of 0 to 14. Notice the inverse relationship between the pH and pOH scales.
For any neutral solution, pH + pOH = 14.00 (at 25°C) and
Figure 16.1 The Inverse Relationship between the pH and pOH Scales
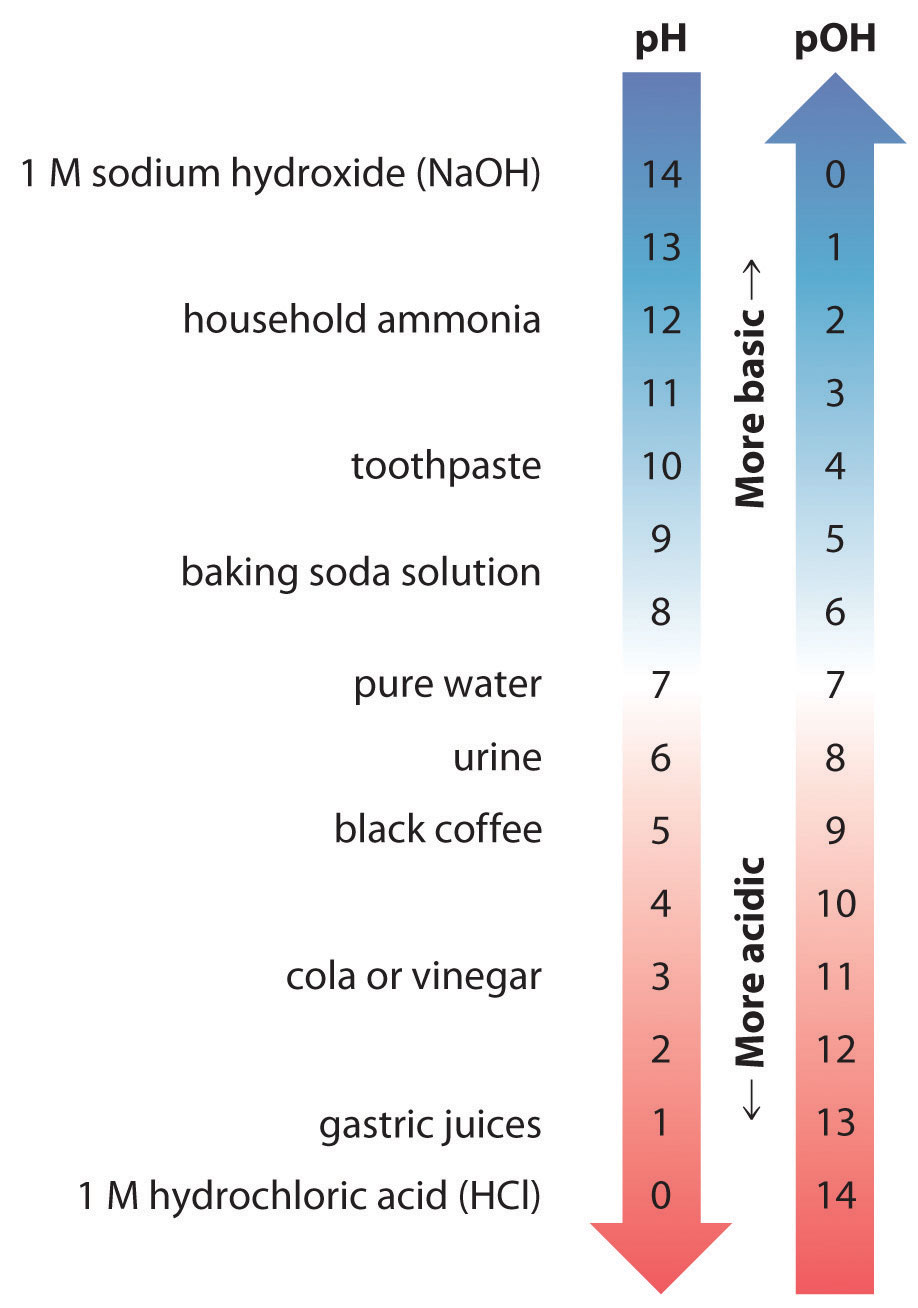
As pH decreases, [H+] and the acidity increase. As pOH increases, [OH−] and the basicity decrease. Common substances have pH values that range from extremely acidic to extremely basic.
The Kw for water at 100°C is 4.99 × 10−13. Calculate pKw for water at this temperature and the pH and the pOH for a neutral aqueous solution at 100°C. Report pH and pOH values to two decimal places.
Given: K w
Asked for: pKw, pH, and pOH
Strategy:
A Calculate pKw by taking the negative logarithm of Kw.
B For a neutral aqueous solution, [H3O+] = [OH−]. Use this relationship and Equation 16.7 to calculate [H3O+] and [OH−]. Then determine the pH and the pOH for the solution.
Solution:
A Because pKw is the negative logarithm of Kw, we can write
pKw = −log Kw = −log(4.99 × 10−13) = 12.302The answer is reasonable: Kw is between 10−13 and 10−12, so pKw must be between 12 and 13.
B Equation 16.7 shows that Kw = [H3O+][OH−]. Because [H3O+] = [OH−] in a neutral solution, we can let x = [H3O+] = [OH−]:
Because x is equal to both [H3O+] and [OH−],
pH = pOH = −log(7.06 × 10−7) = 6.15 (to two decimal places)We could obtain the same answer more easily (without using logarithms) by using the pKw. In this case, we know that pKw = 12.302, and from Equation 16.13, we know that pKw = pH + pOH. Because pH = pOH in a neutral solution, we can use Equation 16.13 directly, setting pH = pOH = y. Solving to two decimal places we obtain the following:
Exercise
Humans maintain an internal temperature of about 37°C. At this temperature, Kw = 3.55 × 10−14. Calculate pKw and the pH and the pOH of a neutral solution at 37°C. Report pH and pOH values to two decimal places.
Answer: pKw = 13.45 pH = pOH = 6.73
Water is amphiprotic: it can act as an acid by donating a proton to a base to form the hydroxide ion, or as a base by accepting a proton from an acid to form the hydronium ion (H3O+). The autoionization of liquid water produces OH− and H3O+ ions. The equilibrium constant for this reaction is called the ion-product constant of liquid water (Kw) and is defined as Kw = [H3O+][OH−]. At 25°C, Kw is 1.01 × 10−14; hence pH + pOH = pKw = 14.00.
Ion-product constant of liquid water
Equation 16.7: Kw = [H3O+][OH−]
Definition of pH
Equation 16.9: pH = −log10[H+]
Equation 16.10: [H+] = 10−pH
Definition of pOH
Equation 16.11: pOH = −log10[OH+]
Equation 16.12: [OH−] = 10−pOH
Relationship among pH, pOH, and p K w
Equation 16.13: pKw= pH + pOH
What is the relationship between the value of the equilibrium constant for the autoionization of liquid water and the tabulated value of the ion-product constant of liquid water (Kw)?
The density of liquid water decreases as the temperature increases from 25°C to 50°C. Will this effect cause Kw to increase or decrease? Why?
Show that water is amphiprotic by writing balanced chemical equations for the reactions of water with HNO3 and NH3. In which reaction does water act as the acid? In which does it act as the base?
Write a chemical equation for each of the following.
Show that K for the sum of the following reactions is equal to Kw.
Kauto = [H3O+][OH−]/[H2O]2 Kw = [H3O+][OH−] = Kauto[H2O]2
The autoionization of sulfuric acid can be described by the following chemical equation:
At 25°C, K = 3 × 10−4. Write an equilibrium constant expression for that is analogous to Kw. The density of H2SO4 is 1.8 g/cm3 at 25°C. What is the concentration of H3SO4+? What fraction of H2SO4 is ionized?
An aqueous solution of a substance is found to have [H3O]+ = 2.48 × 10−8 M. Is the solution acidic, neutral, or basic?
The pH of a solution is 5.63. What is its pOH? What is the [OH−]? Is the solution acidic or basic?
State whether each solution is acidic, neutral, or basic.
Calculate the pH and the pOH of each solution.
Calculate the pH and the pOH of each solution.
The pH of stomach acid is approximately 1.5. What is the [H+]?
Given the pH values in parentheses, what is the [H+] of each solution?
A reaction requires the addition of 250.0 mL of a solution with a pH of 3.50. What mass of HCl (in milligrams) must be dissolved in 250 mL of water to produce a solution with this pH?
If you require 333 mL of a pH 12.50 solution, how would you prepare it using a 0.500 M sodium hydroxide stock solution?
[H3SO4+] = 0.3 M; the fraction ionized is 0.02.
pOH = 8.37; [OH−] = 4.3 × 10−9 M; acidic
2.9 mg HCl
We now turn our attention to acid–base reactions to see how the concepts of chemical equilibrium and equilibrium constants can deepen our understanding of this kind of chemical behavior. We begin with a qualitative description of acid–base equilibriums in terms of the Brønsted–Lowry model and then proceed to a quantitative description in Section 16.4 "Quantitative Aspects of Acid–Base Equilibriums".
We discussed the concept of conjugate acid–base pairs in Chapter 4 "Reactions in Aqueous Solution", using the reaction of ammonia, the base, with water, the acid, as an example. In aqueous solutions, acids and bases can be defined in terms of the transfer of a proton from an acid to a base. Thus for every acidic species in an aqueous solution, there exists a species derived from the acid by the loss of a proton. These two species that differ by only a proton constitute a conjugate acid–base pairAn acid and a base that differ by only one hydrogen ion.. For example, in the reaction of HCl with water (Equation 16.1), HCl, the parent acid, donates a proton to a water molecule, the parent base, thereby forming Cl−. Thus HCl and Cl− constitute a conjugate acid–base pair. By convention, we always write a conjugate acid–base pair as the acid followed by its conjugate base. In the reverse reaction, the Cl− ion in solution acts as a base to accept a proton from H3O+, forming H2O and HCl. Thus H3O+ and H2O constitute a second conjugate acid–base pair. In general, any acid–base reaction must contain two conjugate acid–base pairs, which in this case are HCl/Cl− and H3O+/H2O.
All acid–base reactions contain two conjugate acid–base pairs.

Similarly, in the reaction of acetic acid with water, acetic acid donates a proton to water, which acts as the base. In the reverse reaction, H3O+ is the acid that donates a proton to the acetate ion, which acts as the base. Once again, we have two conjugate acid–base pairs: the parent acid and its conjugate base (CH3CO2H/CH3CO2−) and the parent base and its conjugate acid (H3O+/H2O).

In the reaction of ammonia with water to give ammonium ions and hydroxide ions (Equation 16.3), ammonia acts as a base by accepting a proton from a water molecule, which in this case means that water is acting as an acid. In the reverse reaction, an ammonium ion acts as an acid by donating a proton to a hydroxide ion, and the hydroxide ion acts as a base. The conjugate acid–base pairs for this reaction are NH4+/NH3 and H2O/OH−. Some common conjugate acid–base pairs are shown in Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs".
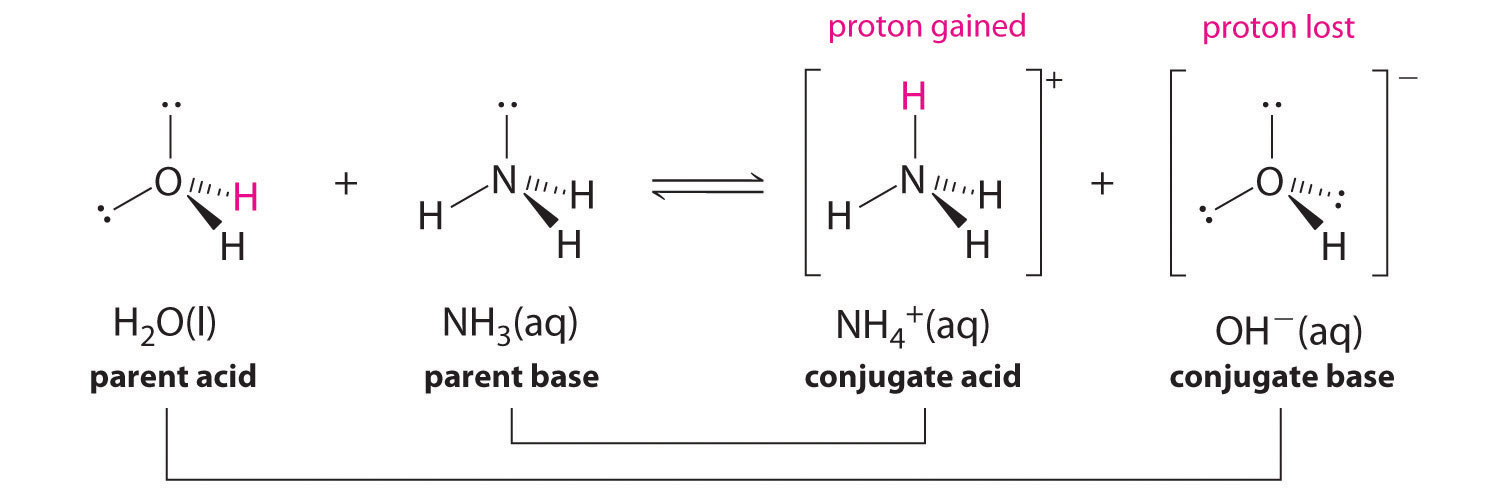
Figure 16.2 The Relative Strengths of Some Common Conjugate Acid–Base Pairs
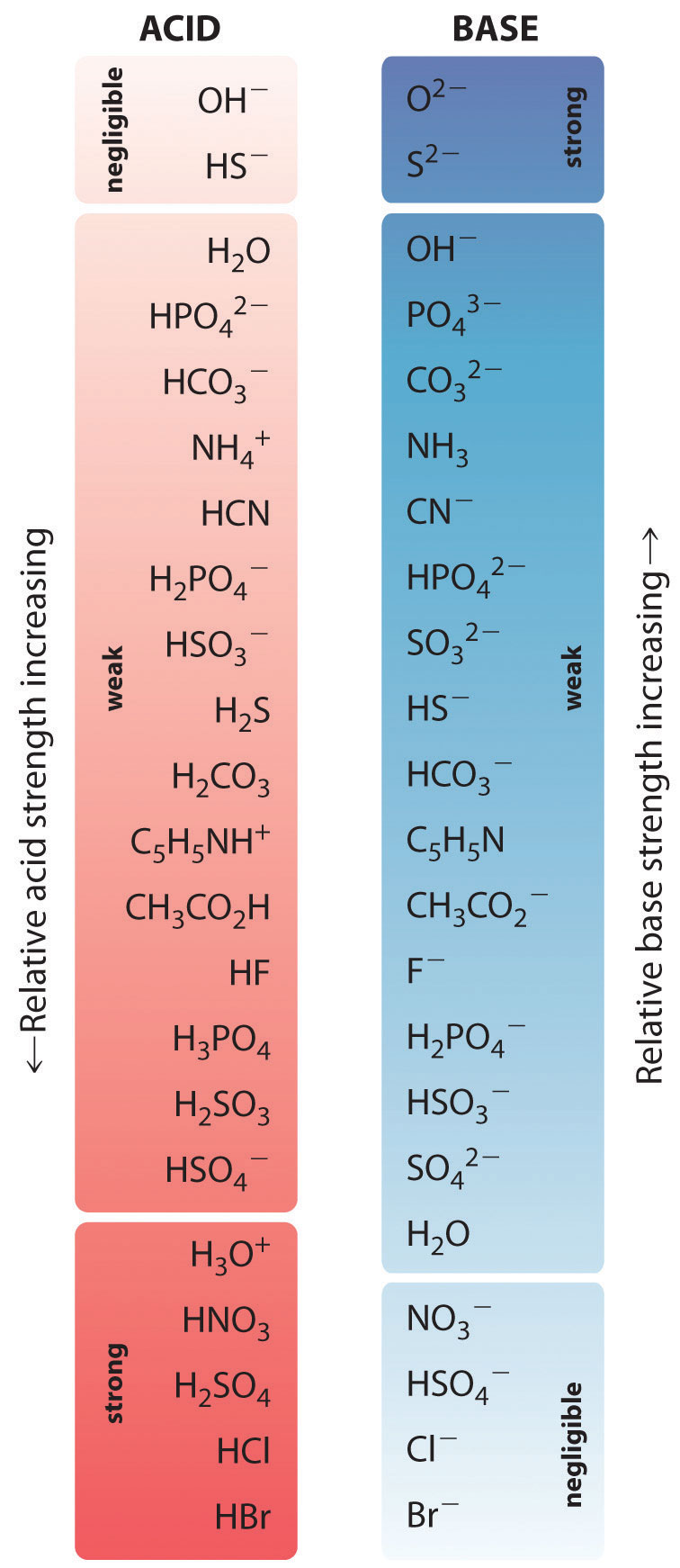
The strongest acids are at the bottom left, and the strongest bases are at the top right. The conjugate base of a strong acid is a very weak base, and, conversely, the conjugate acid of a strong base is a very weak acid.
The magnitude of the equilibrium constant for an ionization reaction can be used to determine the relative strengths of acids and bases. For example, the general equation for the ionization of a weak acid in water, where HA is the parent acid and A− is its conjugate base, is as follows:
Equation 16.14
The equilibrium constant for this dissociation is as follows:
Equation 16.15
As we noted earlier, the concentration of water is essentially constant for all reactions in aqueous solution, so [H2O] in Equation 16.15 can be incorporated into a new quantity, the acid ionization constant (Ka)An equilibrium constant for the ionization (dissociation) of a weak acid (HA) with water, + ⇌ + in which the concentration of water is treated as a constant: = , also called the acid dissociation constant:
Equation 16.16
Thus the numerical values of K and Ka differ by the concentration of water (55.3 M). Again, for simplicity, H3O+ can be written as H+ in Equation 16.16. Keep in mind, though, that free H+ does not exist in aqueous solutions and that a proton is transferred to H2O in all acid ionization reactions to form H3O+. The larger the Ka, the stronger the acid and the higher the H+ concentration at equilibrium.Like all equilibrium constants, acid–base ionization constants are actually measured in terms of the activities of H+ or OH−, thus making them unitless. The values of Ka for a number of common acids are given in Table 16.2 "Values of ".
Table 16.2 Values of Ka, pKa, Kb, and pKb for Selected Acids (HA) and Their Conjugate Bases (A−)
| Acid | HA | K a | pKa | A− | K b | pKb |
|---|---|---|---|---|---|---|
| hydroiodic acid | HI | 2 × 109 | −9.3 | I− | 5.5 × 10−24 | 23.26 |
| sulfuric acid (1)* | H2SO4 | 1 × 102 | −2.0 | HSO4− | 1 × 10−16 | 16.0 |
| nitric acid | HNO3 | 2.3 × 101 | −1.37 | NO3− | 4.3 × 10−16 | 15.37 |
| hydronium ion | H3O+ | 1.0 | 0.00 | H2O | 1.0 × 10−14 | 14.00 |
| sulfuric acid (2)* | HSO4− | 1.0 × 10−2 | 1.99 | SO42− | 9.8 × 10−13 | 12.01 |
| hydrofluoric acid | HF | 6.3 × 10−4 | 3.20 | F− | 1.6 × 10−11 | 10.80 |
| nitrous acid | HNO2 | 5.6 × 10−4 | 3.25 | NO2− | 1.8 × 10−11 | 10.75 |
| formic acid | HCO2H | 1.78 × 10−4 | 3.750 | HCO2− | 5.6 × 10−11 | 10.25 |
| benzoic acid | C6H5CO2H | 6.3 × 10−5 | 4.20 | C6H5CO2− | 1.6 × 10−10 | 9.80 |
| acetic acid | CH3CO2H | 1.7 × 10−5 | 4.76 | CH3CO2− | 5.8 × 10−10 | 9.24 |
| pyridinium ion | C5H5NH+ | 5.9 × 10−6 | 5.23 | C5H5N | 1.7 × 10−9 | 8.77 |
| hypochlorous acid | HOCl | 4.0 × 10−8 | 7.40 | OCl− | 2.5 × 10−7 | 6.60 |
| hydrocyanic acid | HCN | 6.2 × 10−10 | 9.21 | CN− | 1.6 × 10−5 | 4.79 |
| ammonium ion | NH4+ | 5.6 × 10−10 | 9.25 | NH3 | 1.8 × 10−5 | 4.75 |
| water | H2O | 1.0 × 10−14 | 14.00 | OH− | 1.00 | 0.00 |
| acetylene | C2H2 | 1 × 10−26 | 26.0 | HC2− | 1 × 1012 | −12.0 |
| ammonia | NH3 | 1 × 10−35 | 35.0 | NH2− | 1 × 1021 | −21.0 |
| *The number in parentheses indicates the ionization step referred to for a polyprotic acid. | ||||||
Weak bases react with water to produce the hydroxide ion, as shown in the following general equation, where B is the parent base and BH+ is its conjugate acid:
Equation 16.17
The equilibrium constant for this reaction is the base ionization constant (Kb)An equilibrium constant for the reaction of a weak base (B) with water, + ⇌ + in which the concentration of water is treated as a constant: = , also called the base dissociation constant:
Equation 16.18
Once again, the concentration of water is constant, so it does not appear in the equilibrium constant expression; instead, it is included in the Kb. The larger the Kb, the stronger the base and the higher the OH− concentration at equilibrium. The values of Kb for a number of common weak bases are given in Table 16.3 "Values of ".
Table 16.3 Values of Kb, pKb, Ka, and pKa for Selected Weak Bases (B) and Their Conjugate Acids (BH+)
| Base | B | K b | pKb | BH+ | K a | pKa |
|---|---|---|---|---|---|---|
| hydroxide ion | OH− | 1.0 | 0.00* | H2O | 1.0 × 10−14 | 14.00 |
| phosphate ion | PO43− | 2.1 × 10−2 | 1.68 | HPO42− | 4.8 × 10−13 | 12.32 |
| dimethylamine | (CH3)2NH | 5.4 × 10−4 | 3.27 | (CH3)2NH2+ | 1.9 × 10−11 | 10.73 |
| methylamine | CH3NH2 | 4.6 × 10−4 | 3.34 | CH3NH3+ | 2.2 × 10−11 | 10.66 |
| trimethylamine | (CH3)3N | 6.3 × 10−5 | 4.20 | (CH3)3NH+ | 1.6 × 10−10 | 9.80 |
| ammonia | NH3 | 1.8 × 10−5 | 4.75 | NH4+ | 5.6 × 10−10 | 9.25 |
| pyridine | C5H5N | 1.7 × 10−9 | 8.77 | C5H5NH+ | 5.9 × 10−6 | 5.23 |
| aniline | C6H5NH2 | 7.4 × 10−10 | 9.13 | C6H5NH3+ | 1.3 × 10−5 | 4.87 |
| water | H2O | 1.0 × 10−14 | 14.00 | H3O+ | 1.0* | 0.00 |
| *As in Table 16.2 "Values of ". | ||||||
There is a simple relationship between the magnitude of Ka for an acid and Kb for its conjugate base. Consider, for example, the ionization of hydrocyanic acid (HCN) in water to produce an acidic solution, and the reaction of CN− with water to produce a basic solution:
Equation 16.19
Equation 16.20
The equilibrium constant expression for the ionization of HCN is as follows:
Equation 16.21
The corresponding expression for the reaction of cyanide with water is as follows:
Equation 16.22
If we add Equation 16.19 and Equation 16.20, we obtain the following (recall from Chapter 15 "Chemical Equilibrium" that the equilibrium constant for the sum of two reactions is the product of the equilibrium constants for the individual reactions):
In this case, the sum of the reactions described by Ka and Kb is the equation for the autoionization of water, and the product of the two equilibrium constants is Kw:
Equation 16.23
KaKb = KwThus if we know either Ka for an acid or Kb for its conjugate base, we can calculate the other equilibrium constant for any conjugate acid–base pair.
Just as with pH, pOH, and pKw, we can use negative logarithms to avoid exponential notation in writing acid and base ionization constants, by defining pKa as follows:
Equation 16.24
pKa = −log10KaEquation 16.25
and pKb as
Equation 16.26
pKb = −log10KbEquation 16.27
Similarly, Equation 16.23, which expresses the relationship between Ka and Kb, can be written in logarithmic form as follows:
Equation 16.28
pKa + pKb = pKwAt 25°C, this becomes
Equation 16.29
pKa + pKb = 14.00The values of pKa and pKb are given for several common acids and bases in Table 16.2 "Values of " and Table 16.3 "Values of ", respectively, and a more extensive set of data is provided in Chapter 27 "Appendix C: Dissociation Constants and p" and Chapter 28 "Appendix D: Dissociation Constants and p". Because of the use of negative logarithms, smaller values of pKa correspond to larger acid ionization constants and hence stronger acids. For example, nitrous acid (HNO2), with a pKa of 3.25, is about a 1000 times stronger acid than hydrocyanic acid (HCN), with a pKa of 9.21. Conversely, smaller values of pKb correspond to larger base ionization constants and hence stronger bases.
The relative strengths of some common acids and their conjugate bases are shown graphically in Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs". The conjugate acid–base pairs are listed in order (from top to bottom) of increasing acid strength, which corresponds to decreasing values of pKa. This order corresponds to decreasing strength of the conjugate base or increasing values of pKb. At the bottom left of Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs" are the common strong acids; at the top right are the most common strong bases. Notice the inverse relationship between the strength of the parent acid and the strength of the conjugate base. Thus the conjugate base of a strong acid is a very weak base, and the conjugate base of a very weak acid is a strong base.
The conjugate base of a strong acid is a weak base and vice versa.
We can use the relative strengths of acids and bases to predict the direction of an acid–base reaction by following a single rule: an acid–base equilibrium always favors the side with the weaker acid and base, as indicated by these arrows:
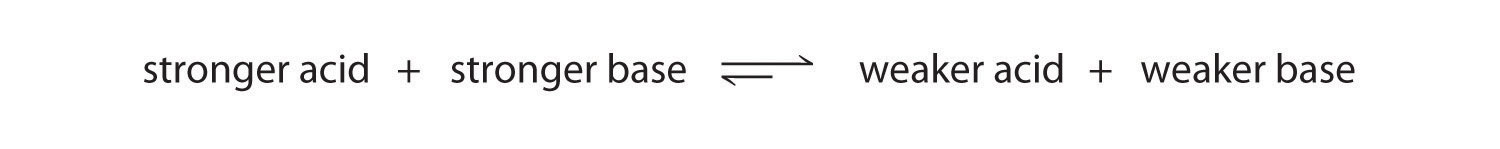
In an acid–base reaction, the proton always reacts with the stronger base.
For example, hydrochloric acid is a strong acid that ionizes essentially completely in dilute aqueous solution to produce H3O+ and Cl−; only negligible amounts of HCl molecules remain undissociated. Hence the ionization equilibrium lies virtually all the way to the right, as represented by a single arrow:
Equation 16.30
In contrast, acetic acid is a weak acid, and water is a weak base. Consequently, aqueous solutions of acetic acid contain mostly acetic acid molecules in equilibrium with a small concentration of H3O+ and acetate ions, and the ionization equilibrium lies far to the left, as represented by these arrows:
Figure 16.3
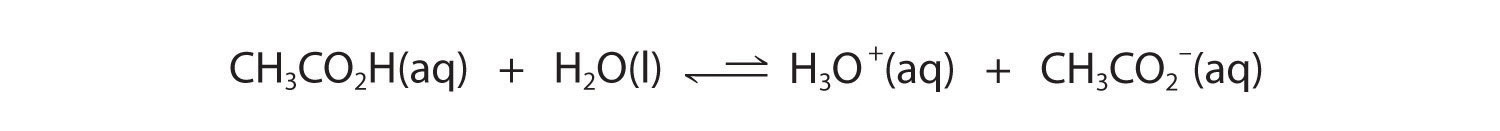
Similarly, in the reaction of ammonia with water, the hydroxide ion is a strong base, and ammonia is a weak base, whereas the ammonium ion is a stronger acid than water. Hence this equilibrium also lies to the left:
Figure 16.4
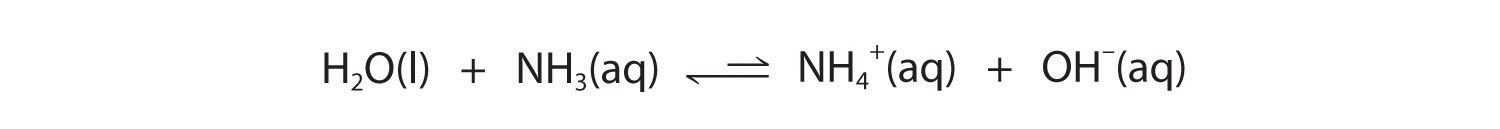
All acid–base equilibriums favor the side with the weaker acid and base. Thus the proton is bound to the stronger base.
Given: pKa and Kb
Asked for: corresponding Kb and pKb, Ka and pKa
Strategy:
The constants Ka and Kb are related as shown in Equation 16.23. The pKa and pKb for an acid and its conjugate base are related as shown in Equation 16.28 and Equation 16.29. Use the relationships pK = −log K and K = 10−pK (Equation 16.24 and Equation 16.26) to convert between Ka and pKa or Kb and pKb.
Solution:
We are given the pKa for butyric acid and asked to calculate the Kb and the pKb for its conjugate base, the butyrate ion. Because the pKa value cited is for a temperature of 25°C, we can use Equation 16.29: pKa + pKb = pKw = 14.00. Substituting the pKa and solving for the pKb,
Because pKb = −log Kb, Kb is 10−9.17 = 6.8 × 10−10.
In this case, we are given Kb for a base (dimethylamine) and asked to calculate Ka and pKa for its conjugate acid, the dimethylammonium ion. Because the initial quantity given is Kb rather than pKb, we can use Equation 16.23: KaKb = Kw. Substituting the values of Kb and Kw at 25°C and solving for Ka,
Because pKa = −log Ka, we have pKa = −log(1.9 × 10−11) = 10.72. We could also have converted Kb to pKb to obtain the same answer:
If we are given any one of these four quantities for an acid or a base (Ka, pKa, Kb, or pKb), we can calculate the other three.
Exercise
Lactic acid [CH3CH(OH)CO2H] is responsible for the pungent taste and smell of sour milk; it is also thought to produce soreness in fatigued muscles. Its pKa is 3.86 at 25°C. Calculate Ka for lactic acid and pKb and Kb for the lactate ion.
Answer: Ka = 1.4 × 10−4 for lactic acid; pKb = 10.14 and Kb = 7.2 × 10−11 for the lactate ion
You will notice in Table 16.2 "Values of " that acids like H2SO4 and HNO3 lie above the hydronium ion, meaning that they have pKa values less than zero and are stronger acids than the H3O+ ion.Recall from Chapter 4 "Reactions in Aqueous Solution" that the acidic proton in virtually all oxoacids is bonded to one of the oxygen atoms of the oxoanion. Thus nitric acid should properly be written as HONO2. Unfortunately, however, the formulas of oxoacids are almost always written with hydrogen on the left and oxygen on the right, giving HNO3 instead. In fact, all six of the common strong acids that we first encountered in Chapter 4 "Reactions in Aqueous Solution" have pKa values less than zero, which means that they have a greater tendency to lose a proton than does the H3O+ ion. Conversely, the conjugate bases of these strong acids are weaker bases than water. Consequently, the proton-transfer equilibriums for these strong acids lie far to the right, and adding any of the common strong acids to water results in an essentially stoichiometric reaction of the acid with water to form a solution of the H3O+ ion and the conjugate base of the acid.
Although Ka for HI is about 108 greater than Ka for HNO3, the reaction of either HI or HNO3 with water gives an essentially stoichiometric solution of H3O+ and I− or NO3−. In fact, a 0.1 M aqueous solution of any strong acid actually contains 0.1 M H3O+, regardless of the identity of the strong acid. This phenomenon is called the leveling effectThe phenomenon that makes the strongest acid that can exist in water. Any species that is a stronger acid than is leveled to the strength of in aqueous solution.: any species that is a stronger acid than the conjugate acid of water (H3O+) is leveled to the strength of H3O+ in aqueous solution because H3O+ is the strongest acid that can exist in equilibrium with water. Consequently, it is impossible to distinguish between the strengths of acids such as HI and HNO3 in aqueous solution, and an alternative approach must be used to determine their relative acid strengths.
One method is to use a solvent such as anhydrous acetic acid. Because acetic acid is a stronger acid than water, it must also be a weaker base, with a lesser tendency to accept a proton than H2O. Measurements of the conductivity of 0.1 M solutions of both HI and HNO3 in acetic acid show that HI is completely dissociated, but HNO3 is only partially dissociated and behaves like a weak acid in this solvent. This result clearly tells us that HI is a stronger acid than HNO3. The relative order of acid strengths and approximate Ka and pKa values for the strong acids at the top of Table 16.2 "Values of " were determined using measurements like this and different nonaqueous solvents.
In aqueous solutions, [H3O+] is the strongest acid and OH− is the strongest base that can exist in equilibrium with H2O.
The leveling effect applies to solutions of strong bases as well: In aqueous solution, any base stronger than OH− is leveled to the strength of OH− because OH− is the strongest base that can exist in equilibrium with water. Salts such as K2O, NaOCH3 (sodium methoxide), and NaNH2 (sodamide, or sodium amide), whose anions are the conjugate bases of species that would lie below water in Table 16.3 "Values of ", are all strong bases that react essentially completely (and often violently) with water, accepting a proton to give a solution of OH− and the corresponding cation:
Equation 16.31
Equation 16.32
Equation 16.33
Other examples that you may encounter are potassium hydride (KH) and organometallic compounds such as methyl lithium (CH3Li).
As you learned in Chapter 4 "Reactions in Aqueous Solution", polyprotic acids such as H2SO4, H3PO4, and H2CO3 contain more than one ionizable proton, and the protons are lost in a stepwise manner. The fully protonated species is always the strongest acid because it is easier to remove a proton from a neutral molecule than from a negatively charged ion. Thus acid strength decreases with the loss of subsequent protons, and, correspondingly, the pKa increases. Consider H2SO4, for example:
Figure 16.5
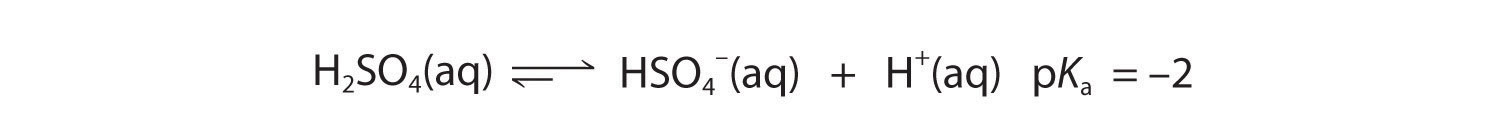
Equation 16.34
The equilibrium in the first reaction lies far to the right, consistent with H2SO4 being a strong acid. In contrast, in the second reaction, appreciable quantities of both HSO4− and SO42− are present at equilibrium.
For a polyprotic acid, acid strength decreases and the pKa increases with the sequential loss of each proton.
The hydrogen sulfate ion (HSO4−) is both the conjugate base of H2SO4 and the conjugate acid of SO42−. Just like water, HSO4− can therefore act as either an acid or a base, depending on whether the other reactant is a stronger acid or a stronger base. Conversely, the sulfate ion (SO42−) is a polyprotic base that is capable of accepting two protons in a stepwise manner:
Figure 16.6
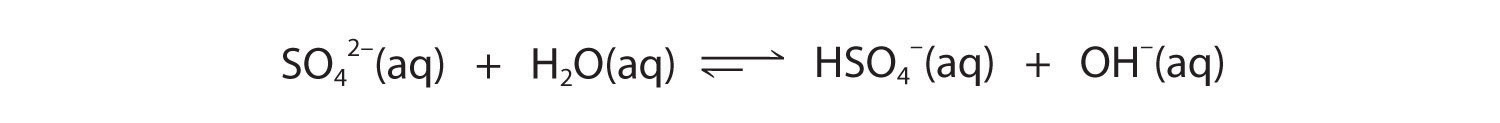
Figure 16.7
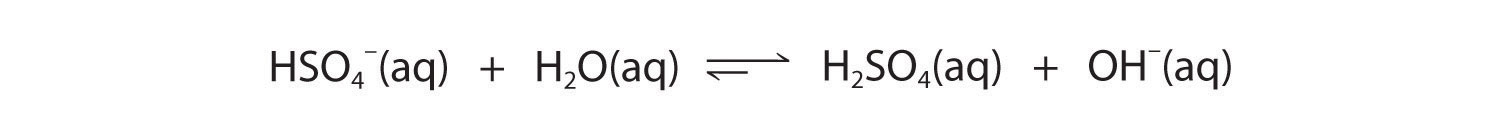
Like any other conjugate acid–base pair, the strengths of the conjugate acids and bases are related by pKa + pKb = pKw. Consider, for example, the HSO4−/ SO42− conjugate acid–base pair. From Table 16.2 "Values of ", we see that the pKa of HSO4− is 1.99. Hence the pKb of SO42− is 14.00 − 1.99 = 12.01. Thus sulfate is a rather weak base, whereas OH− is a strong base, so the equilibrium shown in Figure 16.6 lies to the left. The HSO4− ion is also a very weak base [pKa of H2SO4 = 2.0, pKb of HSO4− = 14 − (−2.0) = 16], which is consistent with what we expect for the conjugate base of a strong acid. Thus the equilibrium shown in Figure 16.7 also lies almost completely to the left. Once again, equilibrium favors the formation of the weaker acid–base pair.
Predict whether the equilibrium for each reaction lies to the left or the right as written.
Given: balanced chemical equation
Asked for: equilibrium position
Strategy:
Identify the conjugate acid–base pairs in each reaction. Then refer to Table 16.2 "Values of ", Table 16.3 "Values of ", and Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs" to determine which is the stronger acid and base. Equilibrium always favors the formation of the weaker acid–base pair.
Solution:
The conjugate acid–base pairs are NH4+/NH3 and HPO42−/PO43−. According to Table 16.2 "Values of " and Table 16.3 "Values of ", NH4+ is a stronger acid (pKa = 9.25) than HPO42− (pKa = 12.32), and PO43− is a stronger base (pKb = 1.68) than NH3 (pKb = 4.75). The equilibrium will therefore lie to the right, favoring the formation of the weaker acid–base pair:
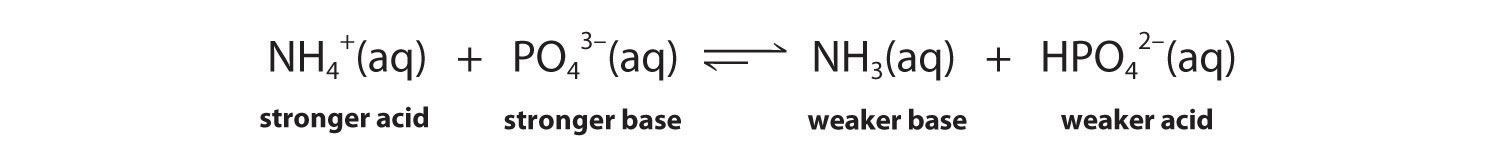
The conjugate acid–base pairs are CH3CH2CO2H/CH3CH2CO2− and HCN/CN−. According to Table 16.2 "Values of ", HCN is a weak acid (pKa = 9.21) and CN− is a moderately weak base (pKb = 4.79). Propionic acid (CH3CH2CO2H) is not listed in Table 16.2 "Values of ", however. In a situation like this, the best approach is to look for a similar compound whose acid–base properties are listed. For example, propionic acid and acetic acid are identical except for the groups attached to the carbon atom of the carboxylic acid (−CH2CH3 versus −CH3), so we might expect the two compounds to have similar acid–base properties. In particular, we would expect the pKa of propionic acid to be similar in magnitude to the pKa of acetic acid. (In fact, the pKa of propionic acid is 4.87, compared to 4.76 for acetic acid, which makes propionic acid a slightly weaker acid than acetic acid.) Thus propionic acid should be a significantly stronger acid than HCN. Because the stronger acid forms the weaker conjugate base, we predict that cyanide will be a stronger base than propionate. The equilibrium will therefore lie to the right, favoring the formation of the weaker acid–base pair:

Exercise
Predict whether the equilibrium for each reaction lies to the left or the right as written.
Answer:
We can also use the relative strengths of conjugate acid–base pairs to understand the acid–base properties of solutions of salts. In Chapter 4 "Reactions in Aqueous Solution", you learned that a neutralization reaction can be defined as the reaction of an acid and a base to produce a salt and water. That is, another cation, such as Na+, replaces the proton on the acid. An example is the reaction of CH3CO2H, a weak acid, with NaOH, a strong base:
Equation 16.35
Depending on the acid–base properties of its component ions, however, a salt can dissolve in water to produce a neutral solution, a basic solution, or an acidic solution.
When a salt such as NaCl dissolves in water, it produces Na+(aq) and Cl−(aq) ions. Using a Lewis approach, the Na+ ion can be viewed as an acid because it is an electron pair acceptor, although its low charge and relatively large radius make it a very weak acid. The Cl− ion is the conjugate base of the strong acid HCl, so it has essentially no basic character. Consequently, dissolving NaCl in water has no effect on the pH of a solution, and the solution remains neutral.
Now let's compare this behavior to the behavior of aqueous solutions of potassium cyanide and sodium acetate. Again, the cations (K+ and Na+) have essentially no acidic character, but the anions (CN− and CH3CO2−) are weak bases that can react with water because they are the conjugate bases of the weak acids HCN and acetic acid, respectively.
Figure 16.8
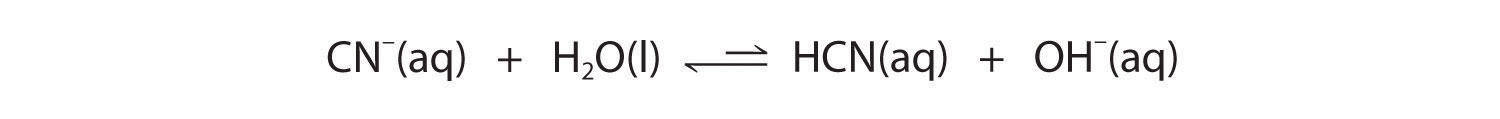
Figure 16.9
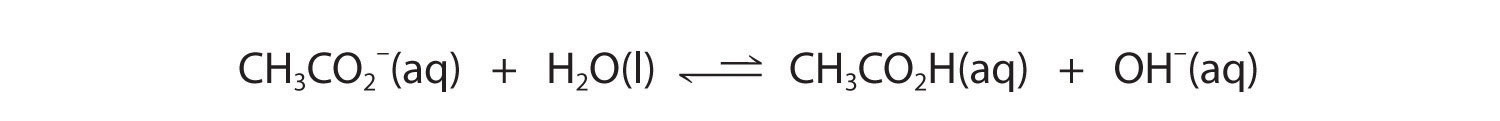
Neither reaction proceeds very far to the right as written because the formation of the weaker acid–base pair is favored. Both HCN and acetic acid are stronger acids than water, and hydroxide is a stronger base than either acetate or cyanide, so in both cases, the equilibrium lies to the left. Nonetheless, each of these reactions generates enough hydroxide ions to produce a basic solution. For example, the pH of a 0.1 M solution of sodium acetate or potassium cyanide at 25°C is 8.8 or 11.1, respectively. From Table 16.2 "Values of " and Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs", we can see that CN− is a stronger base (pKb = 4.79) than acetate (pKb = 9.24), which is consistent with KCN producing a more basic solution than sodium acetate at the same concentration.
In contrast, the conjugate acid of a weak base should be a weak acid (Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs"). For example, ammonium chloride and pyridinium chloride are salts produced by reacting ammonia and pyridine, respectively, with HCl. As you already know, the chloride ion is such a weak base that it does not react with water. In contrast, the cations of the two salts are weak acids that react with water as follows:
Figure 16.10
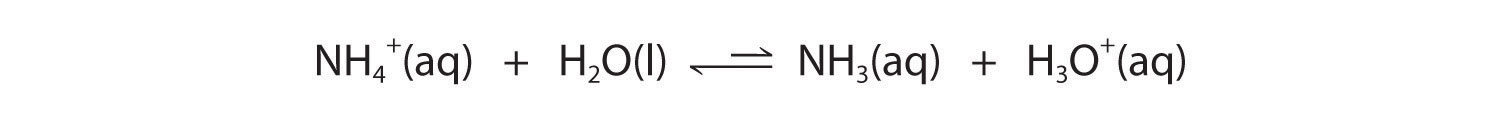
Figure 16.11
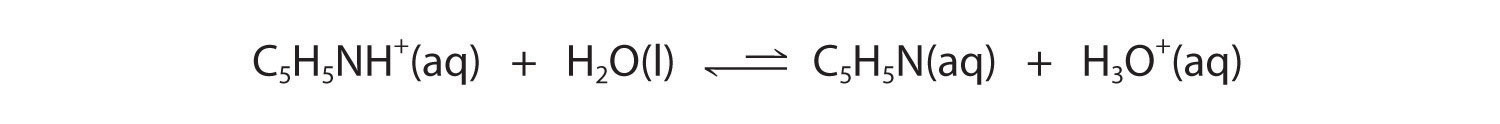
Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs" shows that H3O+ is a stronger acid than either NH4+ or C5H5NH+, and conversely, ammonia and pyridine are both stronger bases than water. The equilibrium will therefore lie far to the left in both cases, favoring the weaker acid–base pair. The H3O+ concentration produced by the reactions is great enough, however, to decrease the pH of the solution significantly: the pH of a 0.10 M solution of ammonium chloride or pyridinium chloride at 25°C is 5.13 or 3.12, respectively. This is consistent with the information shown in Figure 16.2 "The Relative Strengths of Some Common Conjugate Acid–Base Pairs", indicating that the pyridinium ion is more acidic than the ammonium ion.
What happens with aqueous solutions of a salt such as ammonium acetate, where both the cation and the anion can react separately with water to produce an acid and a base, respectively? According to Figure 16.10, the ammonium ion will lower the pH, while according to Figure 16.9, the acetate ion will raise the pH. This particular case is unusual, in that the cation is as strong an acid as the anion is a base (pKa ≈ pKb). Consequently, the two effects cancel, and the solution remains neutral. With salts in which the cation is a stronger acid than the anion is a base, the final solution has a pH < 7.00. Conversely, if the cation is a weaker acid than the anion is a base, the final solution has a pH > 7.00.
Solutions of simple salts of metal ions can also be acidic, even though a metal ion cannot donate a proton directly to water to produce H3O+. Instead, a metal ion can act as a Lewis acid and interact with water, a Lewis base, by coordinating to a lone pair of electrons on the oxygen atom to form a hydrated metal ion (part (a) in Figure 16.12 "Effect of a Metal Ion on the Acidity of Water"), as discussed in Chapter 4 "Reactions in Aqueous Solution". A water molecule coordinated to a metal ion is more acidic than a free water molecule for two reasons. First, repulsive electrostatic interactions between the positively charged metal ion and the partially positively charged hydrogen atoms of the coordinated water molecule make it easier for the coordinated water to lose a proton.
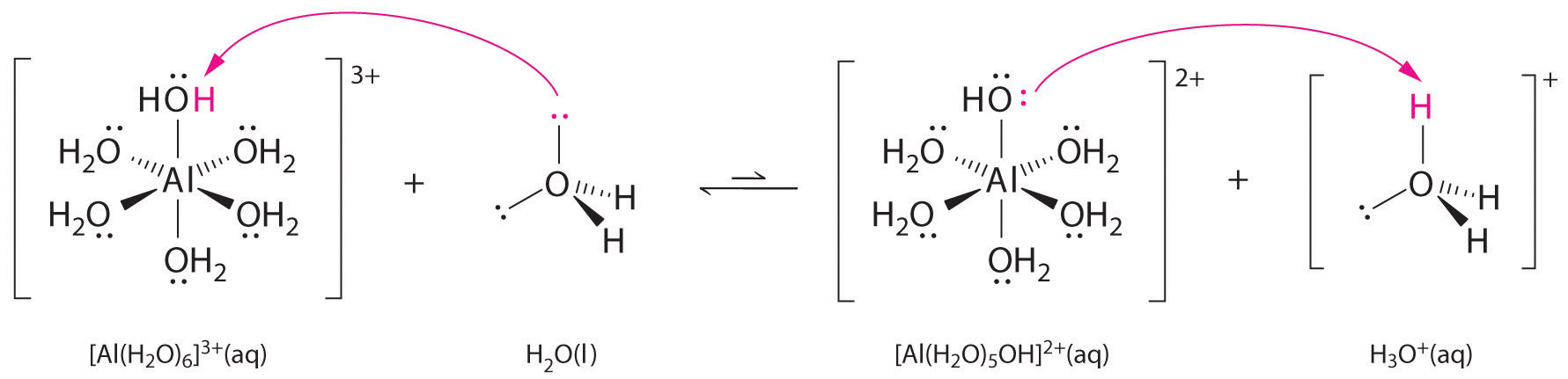
Second, the positive charge on the Al3+ ion attracts electron density from the oxygen atoms of the water molecules, which decreases the electron density in the O–H bonds, as shown in part (b) in Figure 16.12 "Effect of a Metal Ion on the Acidity of Water". With less electron density between the O atoms and the H atoms, the O–H bonds are weaker than in a free H2O molecule, making it easier to lose a H+ ion.
Figure 16.12 Effect of a Metal Ion on the Acidity of Water
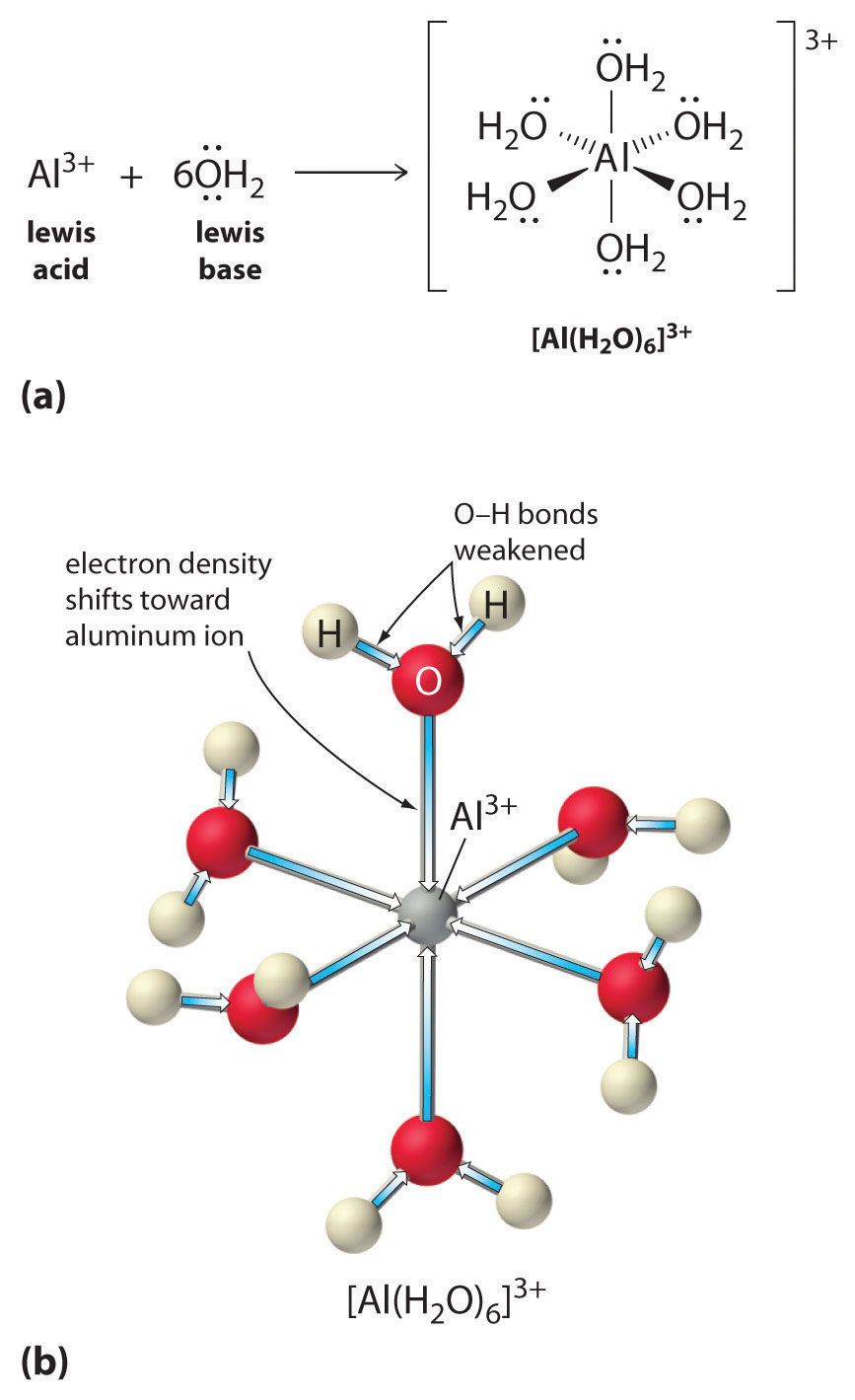
(a) Reaction of the metal ion Al3+ with water to form the hydrated metal ion is an example of a Lewis acid–base reaction. (b) The positive charge on the aluminum ion attracts electron density from the oxygen atoms, which shifts electron density away from the O–H bonds. The decrease in electron density weakens the O–H bonds in the water molecules and makes it easier for them to lose a proton.
The magnitude of this effect depends on the following two factors (Figure 16.13 "The Effect of the Charge and Radius of a Metal Ion on the Acidity of a Coordinated Water Molecule"):
Figure 16.13 The Effect of the Charge and Radius of a Metal Ion on the Acidity of a Coordinated Water Molecule
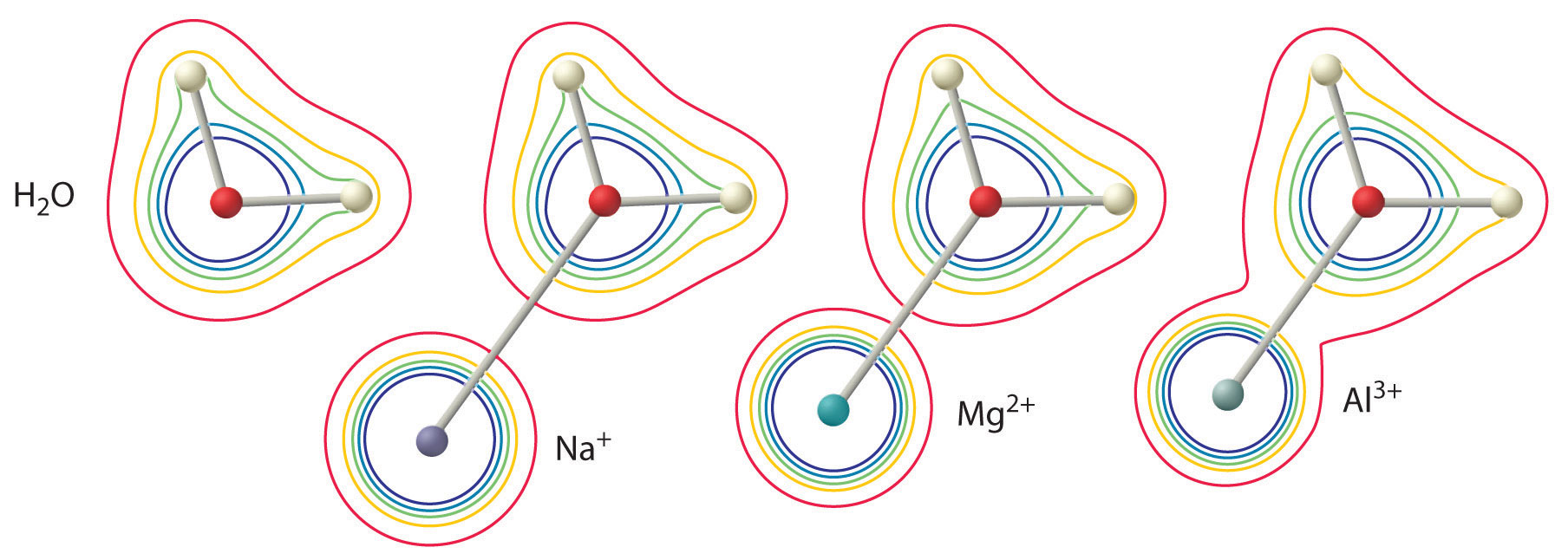
The contours show the electron density on the O atoms and the H atoms in both a free water molecule (left) and water molecules coordinated to Na+, Mg2+, and Al3+ ions. These contour maps demonstrate that the smallest, most highly charged metal ion (Al3+) causes the greatest decrease in electron density of the O–H bonds of the water molecule. Due to this effect, the acidity of hydrated metal ions increases as the charge on the metal ion increases and its radius decreases.
Thus aqueous solutions of small, highly charged metal ions, such as Al3+ and Fe3+, are acidic:
Equation 16.36
The [Al(H2O)6]3+ ion has a pKa of 5.0, making it almost as strong an acid as acetic acid. Because of the two factors described previously, the most important parameter for predicting the effect of a metal ion on the acidity of coordinated water molecules is the charge-to-radius ratio of the metal ion. A number of pairs of metal ions that lie on a diagonal line in the periodic table, such as Li+ and Mg2+ or Ca2+ and Y3+, have different sizes and charges but similar charge-to-radius ratios. As a result, these pairs of metal ions have similar effects on the acidity of coordinated water molecules, and they often exhibit other significant similarities in chemistry as well.
Solutions of small, highly charged metal ions in water are acidic.
Reactions such as those discussed in this section, in which a salt reacts with water to give an acidic or basic solution, are often called hydrolysis reactionsA chemical reaction in which a salt reacts with water to yield an acidic or a basic solution.. Using a separate name for this type of reaction is unfortunate because it suggests that they are somehow different. In fact, hydrolysis reactions are just acid–base reactions in which the acid is a cation or the base is an anion; they obey the same principles and rules as all other acid–base reactions.
A hydrolysis reaction is an acid–base reaction.
Predict whether aqueous solutions of these compounds are acidic, basic, or neutral.
Given: compound
Asked for: acidity or basicity of aqueous solution
Strategy:
A Assess the acid–base properties of the cation and the anion. If the cation is a weak Lewis acid, it will not affect the pH of the solution. If the cation is the conjugate acid of a weak base or a relatively highly charged metal cation, however, it will react with water to produce an acidic solution.
B If the anion is the conjugate base of a strong acid, it will not affect the pH of the solution. If, however, the anion is the conjugate base of a weak acid, the solution will be basic.
Solution:
A The K+ cation has a small positive charge (+1) and a relatively large radius (because it is in the fourth row of the periodic table), so it is a very weak Lewis acid.
B The NO3− anion is the conjugate base of a strong acid, so it has essentially no basic character (Table 16.1 "Definitions of Acids and Bases"). Hence neither the cation nor the anion will react with water to produce H+ or OH−, and the solution will be neutral.
A The Cr3+ ion is a relatively highly charged metal cation that should behave similarly to the Al3+ ion and form the [Cr(H2O)6]3+ complex, which will behave as a weak acid:
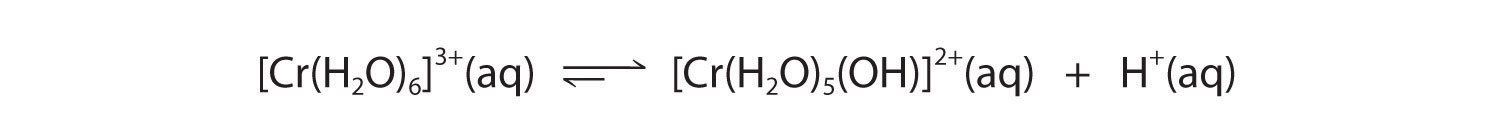
B The Br− anion is a very weak base (it is the conjugate base of the strong acid HBr), so it does not affect the pH of the solution. Hence the solution will be acidic.
A The Na+ ion, like the K+, is a very weak acid, so it should not affect the acidity of the solution.
B In contrast, SO42− is the conjugate base of HSO4−, which is a weak acid. Hence the SO42− ion will react with water as shown in Figure 16.6 to give a slightly basic solution.
Exercise
Predict whether aqueous solutions of the following are acidic, basic, or neutral.
Answer:
Two species that differ by only a proton constitute a conjugate acid–base pair. The magnitude of the equilibrium constant for an ionization reaction can be used to determine the relative strengths of acids and bases. For an aqueous solution of a weak acid, the dissociation constant is called the acid ionization constant (Ka). Similarly, the equilibrium constant for the reaction of a weak base with water is the base ionization constant (Kb). For any conjugate acid–base pair, KaKb = Kw. Smaller values of pKa correspond to larger acid ionization constants and hence stronger acids. Conversely, smaller values of pKb correspond to larger base ionization constants and hence stronger bases. At 25°C, pKa + pKb = 14.00. Acid–base reactions always proceed in the direction that produces the weaker acid–base pair. No acid stronger than H3O+ and no base stronger than OH− can exist in aqueous solution, leading to the phenomenon known as the leveling effect. Polyprotic acids (and bases) lose (and gain) protons in a stepwise manner, with the fully protonated species being the strongest acid and the fully deprotonated species the strongest base. A salt can dissolve in water to produce a neutral, a basic, or an acidic solution, depending on whether it contains the conjugate base of a weak acid as the anion (A−), the conjugate acid of a weak base as the cation (BH+), or both. Salts that contain small, highly charged metal ions produce acidic solutions in water. The reaction of a salt with water to produce an acidic or a basic solution is called a hydrolysis reaction.
Acid ionization constant
Base ionization constant
Relationship between K a and K b of a conjugate acid–base pair
Equation 16.23: KaKb = Kw
Definition of p K a
Equation 16.24: pKa = −log10Ka
Definition of p K b
Equation 16.26: pKa = −log10Ka
Relationship between p K a and p K b of a conjugate acid–base pair
Equation 16.28: pKa + pKb = pKw
Equation 16.29: pKa + pKb = 14.00 (at 25°C)
Identify the conjugate acid–base pairs in each equilibrium.
Identify the conjugate acid–base pairs in each equilibrium.
Salts such as NaH contain the hydride ion (H−). When sodium hydride is added to water, it produces hydrogen gas in a highly vigorous reaction. Write a balanced chemical equation for this reaction and identify the conjugate acid–base pairs.
Write the expression for Ka for each reaction.
Write an expression for the ionization constant Kb for each reaction.
Predict whether each equilibrium lies primarily to the left or to the right.
Species that are strong bases in water, such as CH3−, NH2−, and S2−, are leveled to the strength of OH−, the conjugate base of H2O. Because their relative base strengths are indistinguishable in water, suggest a method for identifying which is the strongest base. How would you distinguish between the strength of the acids HIO3, H2SO4, and HClO4?
Is it accurate to say that a 2.0 M solution of H2SO4, which contains two acidic protons per molecule, is 4.0 M in H+? Explain your answer.
The alkalinity of soil is defined by the following equation: alkalinity = [HCO3−] + 2[CO32−] + [OH−] − [H+]. The source of both HCO3− and CO32− is H2CO3. Explain why the basicity of soil is defined in this way.
Why are aqueous solutions of salts such as CaCl2 neutral? Why is an aqueous solution of NaNH2 basic?
Predict whether aqueous solutions of the following are acidic, basic, or neutral.
When each compound is added to water, would you expect the pH of the solution to increase, decrease, or remain the same?
Which complex ion would you expect to be more acidic—Pb(H2O)42+ or Sn(H2O)42+? Why?
Would you expect Sn(H2O)42+ or Sn(H2O)64+ to be more acidic? Why?
Is it possible to arrange the hydrides LiH, RbH, KH, CsH, and NaH in order of increasing base strength in aqueous solution? Why or why not?
Arrange these acids in order of increasing strength.
Given solutions with the same initial concentration of each acid, which would have the highest percent ionization?
Arrange these bases in order of increasing strength:
Given solutions with the same initial concentration of each base, which would have the highest percent ionization?
Calculate the Ka and the pKa of the conjugate acid of a base with each pKb value.
Benzoic acid is a food preservative with a pKa of 4.20. Determine the Kb and the pKb for the benzoate ion.
Determine Ka and pKa of boric acid [B(OH)3], solutions of which are occasionally used as an eyewash; the pKb of its conjugate base is 4.80.
acid B < acid C < acid A (strongest)
Ka = 6.3 × 10−10 pKa = 9.20
We have seen that the strengths of acids and bases vary over many orders of magnitude. In this section, we explore some of the structural and electronic factors that control the acidity or basicity of a molecule.
In general, the stronger the A–H or B–H+ bond, the less likely the bond is to break to form H+ ions and thus the less acidic the substance. This effect can be illustrated using the hydrogen halides:
| Relative Acid Strength | HF | < | HCl | < | HBr | < | HI |
|---|---|---|---|---|---|---|---|
| H–X Bond Energy (kJ/mol) | 570 | 432 | 366 | 298 | |||
| pKa | 3.20 | −6.1 | −8.9 | −9.3 |
The trend in bond energies is due to a steady decrease in overlap between the 1s orbital of hydrogen and the valence orbital of the halogen atom as the size of the halogen increases. The larger the atom to which H is bonded, the weaker the bond. Thus the bond between H and a large atom in a given family, such as I or Te, is weaker than the bond between H and a smaller atom in the same family, such as F or O. As a result, acid strengths of binary hydrides increase as we go down a column of the periodic table. For example, the order of acidity for the binary hydrides of Group 16 is as follows, with pKa values in parentheses: H2O (14.00 = pKw) < H2S (7.05) < H2Se (3.89) < H2Te (2.6).
Whether we write an acid–base reaction as or as the conjugate base (A− or B) contains one more lone pair of electrons than the parent acid (AH or BH+). Any factor that stabilizes the lone pair on the conjugate base favors dissociation of H+ and makes the parent acid a stronger acid. Let’s see how this explains the relative acidity of the binary hydrides of the elements in the second row of the periodic table. The observed order of increasing acidity is the following, with pKa values in parentheses: CH4 (~50) << NH3 (~36) < H2O (14.00) < HF (3.20). Consider, for example, the compounds at both ends of this series: methane and hydrogen fluoride. The conjugate base of CH4 is CH3−, and the conjugate base of HF is F−. Because fluorine is much more electronegative than carbon, fluorine can better stabilize the negative charge in the F− ion than carbon can stabilize the negative charge in the CH3− ion. Consequently, HF has a greater tendency to dissociate to form H+ and F− than does methane to form H+ and CH3−, making HF a much stronger acid than CH4.
The same trend is predicted by analyzing the properties of the conjugate acids. For a series of compounds of the general formula HE, as the electronegativity of E increases, the E–H bond becomes more polar, favoring dissociation to form E− and H+. Due to both the increasing stability of the conjugate base and the increasing polarization of the E–H bond in the conjugate acid, acid strengths of binary hydrides increase as we go from left to right across a row of the periodic table.
Acid strengths of binary hydrides increase as we go down a column or from left to right across a row of the periodic table.
Atoms or groups of atoms in a molecule other than those to which H is bonded can induce a change in the distribution of electrons within the molecule. This is called an inductive effect, and, much like the coordination of water to a metal ion, it can have a major effect on the acidity or basicity of the molecule. For example, the hypohalous acids (general formula HOX, with X representing a halogen) all have a hydrogen atom bonded to an oxygen atom. In aqueous solution, they all produce the following equilibrium:
Equation 16.37
The acidities of these acids vary by about three orders of magnitude, however, due to the difference in electronegativity of the halogen atoms:
| HOX | Electronegativity of X | pKa |
|---|---|---|
| HOCl | 3.0 | 7.40 |
| HOBr | 2.8 | 8.55 |
| HOI | 2.5 | 10.5 |
As the electronegativity of X increases, the distribution of electron density within the molecule changes: the electrons are drawn more strongly toward the halogen atom and, in turn, away from the H in the O–H bond, thus weakening the O–H bond and allowing dissociation of hydrogen as H+.
The acidity of oxoacids, with the general formula HOXOn (n = 0−3), depends strongly on the number of terminal oxygen atoms attached to the central atom X. As shown in Figure 16.14 "The Relationship between the Acid Strengths of the Oxoacids of Chlorine and the Electron Density on the O–H Unit", the Ka values of the oxoacids of chlorine increase by a factor of about 104 to 106 with each oxygen as successive oxygen atoms are added. The increase in acid strength with increasing number of terminal oxygen atoms is due to both an inductive effect and increased stabilization of the conjugate base.
Any inductive effect that withdraws electron density from an O–H bond increases the acidity of the compound.
Because oxygen is the second most electronegative element, adding terminal oxygen atoms causes electrons to be drawn away from the O–H bond, making it weaker and thereby increasing the strength of the acid. The colors in Figure 16.14 "The Relationship between the Acid Strengths of the Oxoacids of Chlorine and the Electron Density on the O–H Unit" show how the electrostatic potential, a measure of the strength of the interaction of a point charge at any place on the surface of the molecule, changes as the number of terminal oxygen atoms increases. In Figure 16.14 "The Relationship between the Acid Strengths of the Oxoacids of Chlorine and the Electron Density on the O–H Unit" and Figure 16.15 "The Relationship between Delocalization of the Negative Charge in the Oxoanions of Chlorine and the Number of Terminal Oxygen Atoms", blue corresponds to low electron densities, while red corresponds to high electron densities. The oxygen atom in the O–H unit becomes steadily less red from HClO to HClO4 (also written as HOClO3), while the H atom becomes steadily bluer, indicating that the electron density on the O–H unit decreases as the number of terminal oxygen atoms increases. The decrease in electron density in the O–H bond weakens it, making it easier to lose hydrogen as H+ ions, thereby increasing the strength of the acid.
Figure 16.14 The Relationship between the Acid Strengths of the Oxoacids of Chlorine and the Electron Density on the O–H Unit
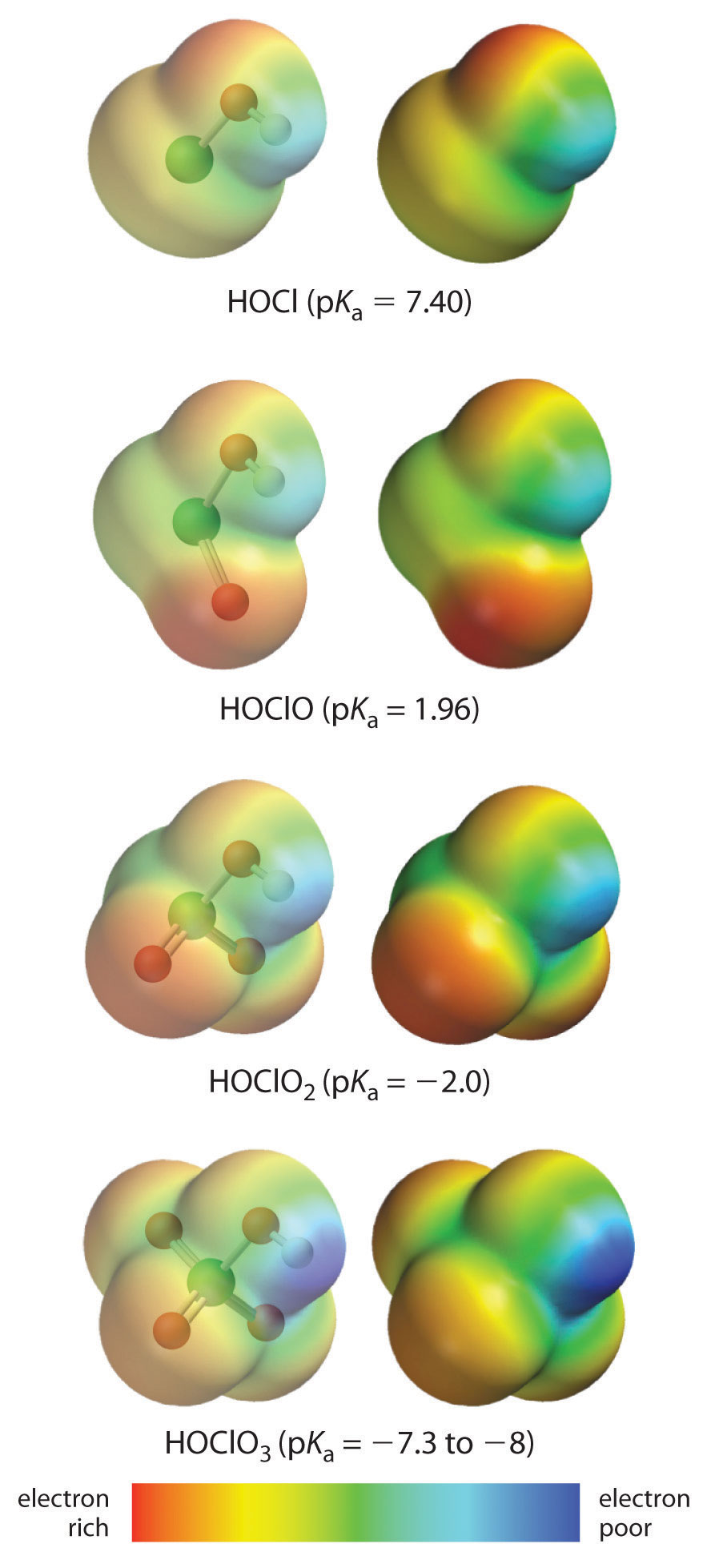
These electrostatic potential maps show how the electron density on the O–H unit decreases as the number of terminal oxygen atoms increases. Blue corresponds to low electron densities, whereas red corresponds to high electron densities.
Source: Chlorine oxoacids pKa values from J. R. Bowser, Inorganic Chemistry (Pacific Grove, CA: Brooks-Cole,1993).
At least as important, however, is the effect of delocalization of the negative charge in the conjugate base. As shown in Figure 16.15 "The Relationship between Delocalization of the Negative Charge in the Oxoanions of Chlorine and the Number of Terminal Oxygen Atoms", the number of resonance structures that can be written for the oxoanions of chlorine increases as the number of terminal oxygen atoms increases, allowing the single negative charge to be delocalized over successively more oxygen atoms. The electrostatic potential plots in Figure 16.15 "The Relationship between Delocalization of the Negative Charge in the Oxoanions of Chlorine and the Number of Terminal Oxygen Atoms" demonstrate that the electron density on the terminal oxygen atoms decreases steadily as their number increases. The oxygen atom in ClO− is red, indicating that it is electron rich, and the color of oxygen progressively changes to green in ClO4−, indicating that the oxygen atoms are becoming steadily less electron rich through the series. For example, in the perchlorate ion (ClO4−), the single negative charge is delocalized over all four oxygen atoms, whereas in the hypochlorite ion (OCl−), the negative charge is largely localized on a single oxygen atom (Figure 16.15 "The Relationship between Delocalization of the Negative Charge in the Oxoanions of Chlorine and the Number of Terminal Oxygen Atoms"). As a result, the perchlorate ion has no localized negative charge to which a proton can bind. Consequently, the perchlorate anion has a much lower affinity for a proton than does the hypochlorite ion, and perchloric acid is one of the strongest acids known.
Electron delocalization in the conjugate base increases acid strength.
Figure 16.15 The Relationship between Delocalization of the Negative Charge in the Oxoanions of Chlorine and the Number of Terminal Oxygen Atoms
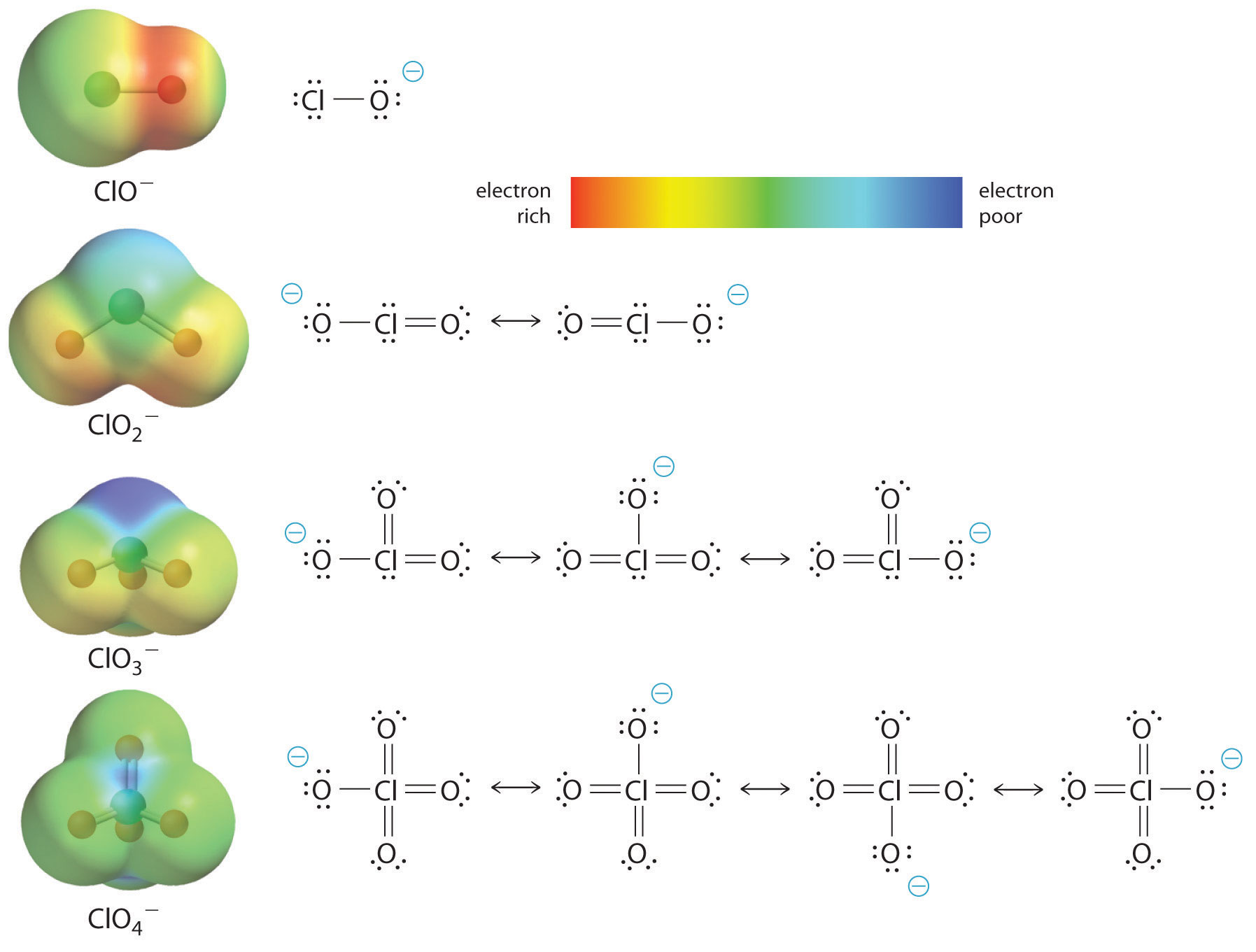
As the number of terminal oxygen atoms increases, the number of resonance structures that can be written for the oxoanions of chlorine also increases, and the single negative charge is delocalized over more oxygen atoms. As these electrostatic potential plots demonstrate, the electron density on the terminal oxygen atoms decreases steadily as their number increases. As the electron density on the oxygen atoms decreases, so does their affinity for a proton, making the anion less basic. As a result, the parent oxoacid is more acidic.
Similar inductive effects are also responsible for the trend in the acidities of oxoacids that have the same number of oxygen atoms as we go across a row of the periodic table from left to right. For example, H3PO4 is a weak acid, H2SO4 is a strong acid, and HClO4 is one of the strongest acids known. The number of terminal oxygen atoms increases steadily across the row, consistent with the observed increase in acidity. In addition, the electronegativity of the central atom increases steadily from P to S to Cl, which causes electrons to be drawn from oxygen to the central atom, weakening the O–H bond and increasing the strength of the oxoacid.
Careful inspection of the data in Table 16.4 "Values of p" shows two apparent anomalies: carbonic acid and phosphorous acid. If carbonic acid (H2CO3) were a discrete molecule with the structure (HO)2C=O, it would have a single terminal oxygen atom and should be comparable in acid strength to phosphoric acid (H3PO4), for which pKa1 = 2.16. Instead, the tabulated value of pKa1 for carbonic acid is 6.35, making it about 10,000 times weaker than expected. As we shall see in Section 16.6 "Buffers", however, H2CO3 is only a minor component of the aqueous solutions of CO2 that are referred to as carbonic acid. Similarly, if phosphorous acid (H3PO3) actually had the structure (HO)3P, it would have no terminal oxygen atoms attached to phosphorous. It would therefore be expected to be about as strong an acid as HOCl (pKa = 7.40). In fact, the pKa1 for phosphorous acid is 1.30, and the structure of phosphorous acid is (HO)2P(=O)H with one H atom directly bonded to P and one P=O bond. Thus the pKa1 for phosphorous acid is similar to that of other oxoacids with one terminal oxygen atom, such as H3PO4. Fortunately, phosphorous acid is the only common oxoacid in which a hydrogen atom is bonded to the central atom rather than oxygen.
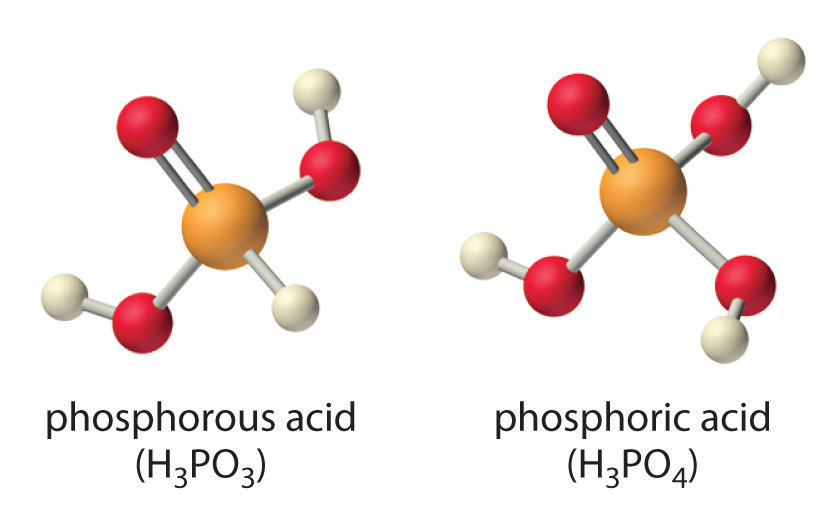
Table 16.4 Values of pKa for Selected Polyprotic Acids and Bases
| Polyprotic Acids | Formula | p K a1 | p K a2 | p K a3 |
| carbonic acid* | “H2CO3” | 6.35 | 10.33 | |
| citric acid | HO2CCH2C(OH)(CO2H)CH2CO2H | 3.13 | 4.76 | 6.40 |
| malonic acid | HO2CCH2CO2H | 2.85 | 5.70 | |
| oxalic acid | HO2CCO2H | 1.25 | 3.81 | |
| phosphoric acid | H3PO4 | 2.16 | 7.21 | 12.32 |
| phosphorous acid | H3PO3 | 1.3 | 6.70 | |
| succinic acid | HO2CCH2CH2CO2H | 4.21 | 5.64 | |
| sulfuric acid | H2SO4 | −2.0 | 1.99 | |
| sulfurous acid* | “H2SO3” | 1.85 | 7.21 | |
| Polyprotic Bases | Formula | p K b1 | p K b2 | |
| ethylenediamine | H2N(CH2)2NH2 | 4.08 | 7.14 | |
| piperazine | HN(CH2CH2)2NH | 4.27 | 8.67 | |
| propylenediamine | H2N(CH2)3NH2 | 3.45 | 5.12 | |
| *H2CO3 and H2SO3 are at best minor components of aqueous solutions of CO2(g) and SO2(g), respectively, but such solutions are commonly referred to as containing carbonic acid and sulfurous acid, respectively. | ||||
|---|---|---|---|---|
Inductive effects are also observed in organic molecules that contain electronegative substituents. The magnitude of the electron-withdrawing effect depends on both the nature and the number of halogen substituents, as shown by the pKa values for several acetic acid derivatives:
As you might expect, fluorine, which is more electronegative than chlorine, causes a larger effect than chlorine, and the effect of three halogens is greater than the effect of two or one. Notice from these data that inductive effects can be quite large. For instance, replacing the –CH3 group of acetic acid by a –CF3 group results in about a 10,000-fold increase in acidity!
Arrange the compounds of each series in order of increasing acid or base strength.
The structures are shown here.
Given: series of compounds
Asked for: relative acid or base strengths
Strategy:
Use relative bond strengths, the stability of the conjugate base, and inductive effects to arrange the compounds in order of increasing tendency to ionize in aqueous solution.
Solution:
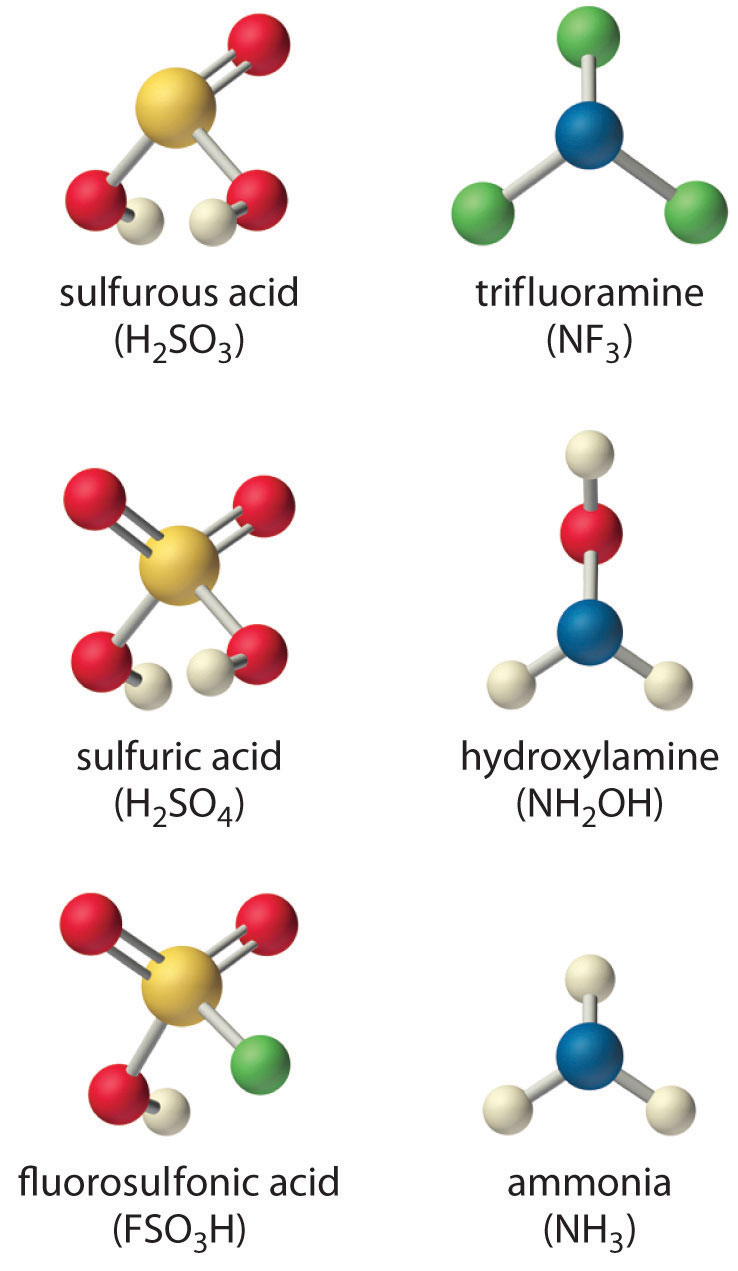
Although both sulfuric acid and sulfurous acid have two –OH groups, the sulfur atom in sulfuric acid is bonded to two terminal oxygen atoms versus one in sulfurous acid. Because oxygen is highly electronegative, sulfuric acid is the stronger acid because the negative charge on the anion is stabilized by the additional oxygen atom. In comparing sulfuric acid and fluorosulfonic acid, we note that fluorine is more electronegative than oxygen. Thus replacing an –OH by –F will remove more electron density from the central S atom, which will, in turn, remove electron density from the S–OH bond and the O–H bond. Because its O–H bond is weaker, FSO3H is a stronger acid than sulfuric acid. The predicted order of acid strengths given here is confirmed by the measured pKa values for these acids:
The structures of both trifluoramine and hydroxylamine are similar to that of ammonia. In trifluoramine, all of the hydrogen atoms in NH3 are replaced by fluorine atoms, whereas in hydroxylamine, one hydrogen atom is replaced by OH. Replacing the three hydrogen atoms by fluorine will withdraw electron density from N, making the lone electron pair on N less available to bond to an H+ ion. Thus NF3 is predicted to be a much weaker base than NH3. Similarly, because oxygen is more electronegative than hydrogen, replacing one hydrogen atom in NH3 by OH will make the amine less basic. Because oxygen is less electronegative than fluorine and only one hydrogen atom is replaced, however, the effect will be smaller. The predicted order of increasing base strength shown here is confirmed by the measured pKb values:
Trifluoramine is such a weak base that it does not react with aqueous solutions of strong acids. Hence its base ionization constant has not been measured.
Exercise
Arrange the compounds of each series in order of
Answer:
The acid–base strength of a molecule depends strongly on its structure. The weaker the A–H or B–H+ bond, the more likely it is to dissociate to form an H+ ion. In addition, any factor that stabilizes the lone pair on the conjugate base favors the dissociation of H+, making the conjugate acid a stronger acid. Atoms or groups of atoms elsewhere in a molecule can also be important in determining acid or base strength through an inductive effect, which can weaken an O–H bond and allow hydrogen to be more easily lost as H+ ions.
Section 16.3 "Molecular Structure and Acid–Base Strength" presented several factors that affect the relative strengths of acids and bases. For each pair, identify the most important factor in determining which is the stronger acid or base in aqueous solution.
The stability of the conjugate base is an important factor in determining the strength of an acid. Which would you expect to be the stronger acid in aqueous solution—C6H5NH3+ or NH4+? Justify your reasoning.
Explain why H2Se is a weaker acid than HBr.
Arrange the following in order of decreasing acid strength in aqueous solution: H3PO4, CH3PO3H2, and HClO3.
Arrange the following in order of increasing base strength in aqueous solution: CH3S−, OH−, and CF3S−.
Arrange the following in order of increasing acid strength in aqueous solution: HClO2, HNO2, and HNO3.
Do you expect H2SO3 or H2SeO3 to be the stronger acid? Why?
Give a plausible explanation for why CF3OH is a stronger acid than CH3OH in aqueous solution. Do you expect CHCl2CH2OH to be a stronger or a weaker acid than CH3OH? Why?
Do you expect Cl2NH or NH3 to be the stronger base in aqueous solution? Why?
CF3S− < CH3S− < OH− (strongest base)
NH3; Cl atoms withdraw electron density from N in Cl2NH.
This section presents a quantitative approach to analyzing acid–base equilibriums. You will learn how to determine the values of Ka and Kb, how to use Ka or Kb to calculate the percent ionization and the pH of an aqueous solution of an acid or a base, and how to calculate the equilibrium constant for the reaction of an acid with a base from the Ka and Kb of the reactants.
The ionization constants Ka and Kb are equilibrium constants that are calculated from experimentally measured concentrations, just like the equilibrium constants discussed in Chapter 15 "Chemical Equilibrium". Before proceeding further, it is important to understand exactly what is meant when we describe the concentration of an aqueous solution of a weak acid or a weak base. Suppose, for example, we have a bottle labeled 1.0 M acetic acid or 1.0 M ammonia. As you learned in Chapter 4 "Reactions in Aqueous Solution", such a solution is usually prepared by dissolving 1.0 mol of acetic acid or ammonia in water and adding enough water to give a final volume of exactly 1.0 L. If, however, we were to list the actual concentrations of all the species present in either solution, we would find that none of the values is exactly 1.0 M because a weak acid such as acetic acid or a weak base such as ammonia always reacts with water to some extent. The extent of the reaction depends on the Ka or the Kb, the concentration of the acid or the base, and the temperature. Consequently, only the total concentration of both the ionized and unionized species is equal to 1.0 M.
The analytical concentration (C) is defined as the total concentration of all forms of an acid or a base that are present in solution, regardless of their state of protonation. Thus a “1.0 M” solution of acetic acid has an analytical concentration of 1.0 M, which is the sum of the actual concentrations of unionized acetic acid (CH3CO2H) and the ionized form (CH3CO2−):
Equation 16.38
As we shall see shortly, if we know the analytical concentration and the Ka, we can calculate the actual values of [CH3CO2H] and [CH3CO2−].
The equilibrium equations for the reaction of acetic acid and ammonia with water are as follows:
Equation 16.39
Equation 16.40
where Ka and Kb are the ionization constants for acetic acid and ammonia, respectively. In addition to the analytical concentration of the acid (or the base), we must have a way to measure the concentration of at least one of the species in the equilibrium constant expression to determine the Ka (or the Kb). There are two common ways to obtain the concentrations: (1) measure the electrical conductivity of the solution, which is related to the total concentration of ions present, and (2) measure the pH of the solution, which gives [H+] or [OH−].
Example 6 and Example 7 illustrate the procedure for determining Ka for a weak acid and Kb for a weak base. In both cases, we will follow the procedure developed in Chapter 15 "Chemical Equilibrium": the analytical concentration of the acid or the base is the initial concentration, and the stoichiometry of the reaction with water determines the change in concentrations. The final concentrations of all species are calculated from the initial concentrations and the changes in the concentrations. Inserting the final concentrations into the equilibrium constant expression enables us to calculate the Ka or the Kb.
Electrical conductivity measurements indicate that 0.42% of the acetic acid molecules in a 1.00 M solution are ionized at 25°C. Calculate Ka and pKa for acetic acid at this temperature.
Given: analytical concentration and percent ionization
Asked for: Ka and pKa
Strategy:
A Write the balanced equilibrium equation for the reaction and derive the equilibrium constant expression.
B Use the data given and the stoichiometry of the reaction to construct a table showing the initial concentrations, the changes in concentrations, and the final concentrations for all species in the equilibrium constant expression.
C Substitute the final concentrations into the equilibrium constant expression and calculate the Ka. Take the negative logarithm of Ka to obtain the pKa.
Solution:
A The balanced equilibrium equation for the dissociation of acetic acid is as follows:
and the equilibrium constant expression is as follows:
B To calculate the Ka, we need to know the equilibrium concentrations of CH3CO2H, CH3CO2−, and H+. The most direct way to do this is to construct a table that lists the initial concentrations and the changes in concentrations that occur during the reaction to give the final concentrations, using the procedure introduced in Chapter 15 "Chemical Equilibrium". The initial concentration of unionized acetic acid ([CH3CO2H]i) is the analytical concentration, 1.00 M, and the initial acetate concentration ([CH3CO2−]i) is zero. The initial concentration of H+ is not zero, however; [H+]i is 1.00 × 10−7 M due to the autoionization of water. The measured percent ionization tells us that 0.42% of the acetic acid molecules are ionized at equilibrium. Consequently, the change in the concentration of acetic acid is Δ[CH3CO2H] = −(4.2 × 10−3)(1.00 M) = −0.0042 M. Conversely, the change in the acetate concentration is Δ[CH3CO2−] = +0.0042 M because every 1 mol of acetic acid that ionizes gives 1 mol of acetate. Because one proton is produced for each acetate ion formed, Δ[H+] = +0.0042 M as well. These results are summarized in the following table.
| [CH3CO2H] | [H+] | [CH3CO2−] | |
|---|---|---|---|
| initial | 1.00 | 1.00 × 10−7 | 0 |
| change | −0.0042 | +0.0042 | +0.0042 |
| final | |||
The final concentrations of all species are therefore as follows:
C We can now calculate Ka by inserting the final concentrations into the equilibrium constant expression:
The pKa is the negative logarithm of Ka: pKa = −log Ka = −log(1.8 × 10−5) = 4.74.
Exercise
Picric acid is the common name for 2,4,6-trinitrophenol, a derivative of phenol (C6H5OH) in which three H atoms are replaced by nitro (–NO2) groups. The presence of the nitro groups removes electron density from the phenyl ring, making picric acid a much stronger acid than phenol (pKa = 9.99). The nitro groups also make picric acid potentially explosive, as you might expect based on its chemical similarity to 2,4,6-trinitrotoluene, better known as TNT. A 0.20 M solution of picric acid is 73% ionized at 25°C. Calculate Ka and pKa for picric acid.
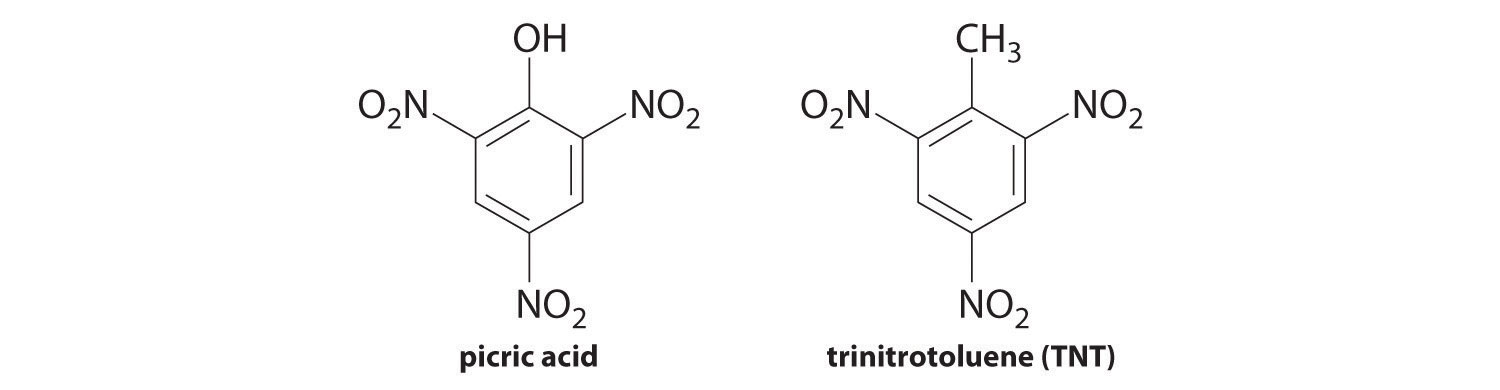
Answer: Ka = 0.39; pKa = 0.41
A 1.0 M aqueous solution of ammonia has a pH of 11.63 at 25°C. Calculate Kb and pKb for ammonia.
Given: analytical concentration and pH
Asked for: Kb and pKb
Strategy:
A Write the balanced equilibrium equation for the reaction and derive the equilibrium constant expression.
B Use the data given and the stoichiometry of the reaction to construct a table showing the initial concentrations, the changes in concentrations, and the final concentrations for all species in the equilibrium constant expression.
C Substitute the final concentrations into the equilibrium constant expression and calculate the Kb. Take the negative logarithm of Kb to obtain the pKb.
Solution:
A The balanced equilibrium equation for the reaction of ammonia with water is as follows:
and the equilibrium constant expression is as follows:
Remember that water does not appear in the equilibrium constant expression for Kb.
B To calculate Kb, we need to know the equilibrium concentrations of NH3, NH4+, and OH−. The initial concentration of NH3 is the analytical concentration, 1.0 M, and the initial concentrations of NH4+ and OH− are 0 M and 1.00 × 10−7 M, respectively. In this case, we are given the pH of the solution, which allows us to calculate the final concentration of one species (OH−) directly, rather than the change in concentration. Recall that pKw = pH + pOH = 14.00 at 25°C. Thus pOH = 14.00 − pH = 14.00 − 11.63 = 2.37, and [OH−]f = 10−2.37 = 4.3 × 10−3 M. Our data thus far are listed in the following table.
| [NH3] | [NH4+] | [OH−] | |
|---|---|---|---|
| initial | 1.0 | 0 | 1.00 × 10−7 |
| change | |||
| final | 4.3 × 10−3 | ||
The final [OH−] is much greater than the initial [H+], so the change in [OH−] is as follows:
Δ[OH−] = (4.3 × 10−3 M) − (1.00 × 10−7 M) ≈ 4.3 × 10−3 MThe stoichiometry of the reaction tells us that 1 mol of NH3 is converted to NH4+ for each 1 mol of OH− formed, so
Δ[NH4+] = +4.3 × 10−3 M and Δ[NH3] = −4.3 ×10−3 MWe can now insert these values for the changes in concentrations into the table, which enables us to complete the table.
| [NH3] | [NH4+] | [OH−] | |
|---|---|---|---|
| initial | 1.0 | 0 | 1.00 × 10−7 |
| change | −4.3 × 10−3 | +4.3 × 10−3 | +4.3 × 10−3 |
| final | 1.0 | 4.3 × 10−3 | 4.3 × 10−3 |
C Inserting the final concentrations into the equilibrium constant expression gives Kb:
and pKb = −log Kb = 4.74.
The Kb and the pKb for ammonia are almost exactly the same as the Ka and the pKa for acetic acid at 25°C. In other words, ammonia is almost exactly as strong a base as acetic acid is an acid. Consequently, the extent of the ionization reaction in an aqueous solution of ammonia at a given concentration is the same as in an aqueous solution of acetic acid at the same concentration.
Exercise
The pH of a 0.050 M solution of pyridine (C6H5N) is 8.96 at 25°C. Calculate Kb and pKb for pyridine.
Answer: Kb = 1.7 × 10−9; pKb = 8.77
When carrying out a laboratory analysis, chemists frequently need to know the concentrations of all species in solution. Because the reactivity of a weak acid or a weak base is usually very different from the reactivity of its conjugate base or acid, we often need to know the percent ionization of a solution of an acid or a base to understand a chemical reaction. The percent ionization is defined as follows:
Equation 16.41
Equation 16.42
One way to determine the concentrations of species in solutions of weak acids and bases is a variation of the tabular method we used previously to determine Ka and Kb values. As a demonstration, we will calculate the concentrations of all species and the percent ionization in a 0.150 M solution of formic acid at 25°C. The data in Table 16.2 "Values of " show that formic acid (Ka = 1.8 × 10−4 at 25°C) is a slightly stronger acid than acetic acid. The equilibrium equation for the ionization of formic acid in water is as follows:
Equation 16.43
and the equilibrium constant expression for this reaction is as follows:
Equation 16.44
We set the initial concentration of HCO2H equal to 0.150 M, and that of HCO2− is 0 M. The initial concentration of H+ is 1.00 × 10−7 M due to the autoionization of water. Because the equilibrium constant for the ionization reaction is small, the equilibrium will lie to the left, favoring the unionized form of the acid. Hence we can define x as the amount of formic acid that dissociates.
If the change in [HCO2H] is −x, then the change in [H+] and [HCO2−] is +x. The final concentration of each species is the sum of its initial concentration and the change in concentration, as summarized in the following table.
| [HCO2H] | [H+] | [HCO2−] | |
|---|---|---|---|
| initial | 0.150 | 1.00 × 10−7 | 0 |
| change | −x | +x | +x |
| final | (0.150 − x) | (1.00 × 10−7 + x) | x |
We can calculate x by substituting the final concentrations from the table into the equilibrium constant expression:
Because the ionization constant Ka is small, x is likely to be small compared with the initial concentration of formic acid: (0.150 − x) M ≈ 0.150 M. Moreover, [H+] due to the autoionization of water (1.00 × 10−7 M) is likely to be negligible compared with [H+] due to the dissociation of formic acid: (1.00 × 10−7 + x) M ≈ x M. Inserting these values into the equilibrium constant expression and solving for x,
We can now calculate the concentrations of the species present in a 0.150 M formic acid solution by inserting this value of x into the expressions in the last line of the table:
Thus the pH of the solution is –log(5.2 × 10−3) = 2.28. We can also use these concentrations to calculate the fraction of the original acid that is ionized. In this case, the percent ionization is the ratio of [H+] (or [HCO2−]) to the analytical concentration, multiplied by 100 to give a percentage:
Always check to make sure that any simplifying assumption was valid. As a general rule of thumb, approximations such as those used here are valid only if the quantity being neglected is no more than about 5% of the quantity to which it is being added or from which it is being subtracted. If the quantity that was neglected is much greater than about 5%, then the approximation is probably not valid, and you should go back and solve the problem using the quadratic formula. In the previous demonstration, both simplifying assumptions were justified: the percent ionization is only 3.5%, which is well below the approximately 5% limit, and the 1.00 × 10−7 M [H+] due to the autoionization of water is much, much less than the 5.2 × 10−3 M [H+] due to the ionization of formic acid.
As a general rule, the [H+] contribution due to the autoionization of water can be ignored as long as the product of the acid or the base ionization constant and the analytical concentration of the acid or the base is at least 10 times greater than the [H+] or [OH−] from the autoionization of water—that is, if
Equation 16.45
KaCHA ≥ 10(1.00 × 10−7) = 1.0 × 10−6or
Equation 16.46
KbCB ≥ 10(1.00 × 10−7) = 1.0 × 10−6By substituting the appropriate values for the formic acid solution into Equation 16.45, we see that the simplifying assumption is valid in this case:
Equation 16.47
KaCHA = (1.8 × 10−4)(0.150) = 2.7 × 10−5 > 1.0 × 10−6Doing this simple calculation before solving this type of problem saves time and allows you to write simplified expressions for the final concentrations of the species present. In practice, it is necessary to include the [H+] contribution due to the autoionization of water only for extremely dilute solutions of very weak acids or bases.
Example 8 illustrates how the procedure outlined previously can be used to calculate the pH of a solution of a weak base.
Calculate the pH and percent ionization of a 0.225 M solution of ethylamine (CH3CH2NH2), which is used in the synthesis of some dyes and medicines. The pKb of ethylamine is 3.19 at 20°C.
Given: concentration and pKb
Asked for: pH and percent ionization
Strategy:
A Write the balanced equilibrium equation for the reaction and the equilibrium constant expression. Calculate Kb from pKb.
B Use Equation 16.45 to see whether you can ignore [H+] due to the autoionization of water. Then use a tabular format to write expressions for the final concentrations of all species in solution. Substitute these values into the equilibrium equation and solve for [OH−]. Use Equation 16.42 to calculate the percent ionization.
C Use the relationship Kw = [OH−][H+] to obtain [H+]. Then calculate the pH of the solution.
Solution:
A We begin by writing the balanced equilibrium equation for the reaction:
The corresponding equilibrium constant expression is as follows:
From the pKb, we have Kb = 10−3.19 = 6.5 × 10−4.
B To calculate the pH, we need to determine the H+ concentration. Unfortunately, H+ does not appear in either the chemical equation or the equilibrium constant expression. However, [H+] and [OH−] in an aqueous solution are related by Kw = [H+][OH−]. Hence if we can determine [OH−], we can calculate [H+] and then the pH. The initial concentration of CH3CH2NH2 is 0.225 M, and the initial [OH−] is 1.00 × 10−7 M. Because ethylamine is a weak base, the extent of the reaction will be small, and it makes sense to let x equal the amount of CH3CH2NH2 that reacts with water. The change in [CH3CH2NH2] is therefore −x, and the change in both [CH3CH2NH3+] and [OH−] is +x. To see whether the autoionization of water can safely be ignored, we substitute Kb and CB into Equation 16.46:
KbCB = (6.5 × 10−4)(0.225) = 1.5 × 10−4 > 1.0 × 10−6Thus the simplifying assumption is valid, and we will not include [OH−] due to the autoionization of water in our calculations.
| [CH3CH2NH2] | [CH3CH2NH3+] | [OH−] | |
|---|---|---|---|
| initial | 0.225 | 0 | 1.00 × 10−7 |
| change | −x | +x | +x |
| final | (0.225 − x) | x | x |
Substituting the quantities from the last line of the table into the equilibrium constant expression,
As before, we assume the amount of CH3CH2NH2 that ionizes is small compared with the initial concentration, so [CH3CH2NH2]f = 0.225 − x ≈ 0.225. With this assumption, we can simplify the equilibrium equation and solve for x:
The percent ionization is therefore
which is at the upper limit of the approximately 5% range that can be ignored. The final hydroxide concentration is thus 0.012 M.
C We can now determine the [H+] using the expression for Kw:
The pH of the solution is −log(8.4 × 10−13) = 12.08. Alternatively, we could have calculated pOH as −log(0.012) = 1.92 and determined the pH as follows:
The two methods are equivalent.
Exercise
Aromatic amines, in which the nitrogen atom is bonded directly to a phenyl ring (−C6H5) tend to be much weaker bases than simple alkylamines. For example, aniline (C6H5NH2) has a pKb of 9.13 at 25°C. What is the pH of a 0.050 M solution of aniline?
Answer: 8.78
The previous examples illustrate a key difference between solutions of strong acids and bases and solutions of weak acids and bases. Because strong acids and bases ionize essentially completely in water, the percent ionization is always approximately 100%, regardless of the concentration. In contrast, the percent ionization in solutions of weak acids and bases is small and depends on the analytical concentration of the weak acid or base. As illustrated for benzoic acid in Figure 16.16 "The Relationship between the Analytical Concentration of a Weak Acid and Percent Ionization", the percent ionization of a weak acid or a weak base actually increases as its analytical concentration decreases. The percent ionization also increases as the magnitude of Ka and Kb increases.
Figure 16.16 The Relationship between the Analytical Concentration of a Weak Acid and Percent Ionization
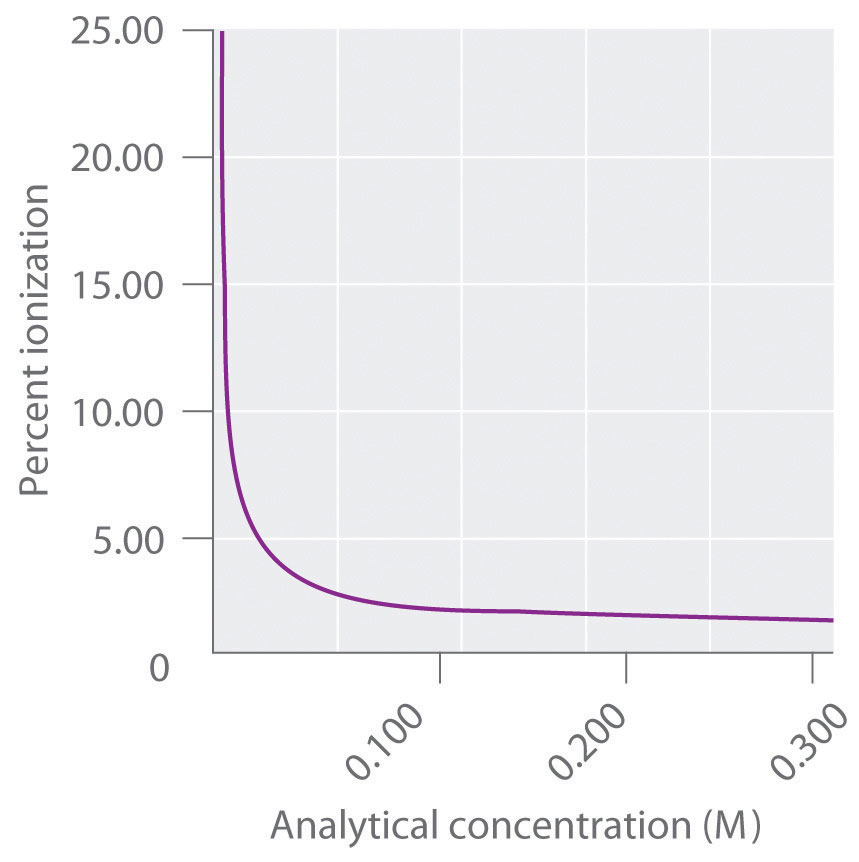
As shown here for benzoic acid (C6H5CO2H), the percent ionization decreases as the analytical concentration of a weak acid increases.
Unlike the Ka or the Kb, the percent ionization is not a constant for weak acids and bases but depends on both the Ka or the Kb and the analytical concentration. Consequently, the procedure in Example 8 must be used to calculate the percent ionization and pH for solutions of weak acids and bases. Example 9 and its corresponding exercise demonstrate that the combination of a dilute solution and a relatively large Ka or Kb can give a percent ionization much greater than 5%, making it necessary to use the quadratic equation to determine the concentrations of species in solution.
The percent ionization in a solution of a weak acid or a weak base increases as the analytical concentration decreases and as the Ka or the Kb increases.
Benzoic acid (C6H5CO2H) is used in the food industry as a preservative and medically as an antifungal agent. Its pKa at 25°C is 4.20, making it a somewhat stronger acid than acetic acid. Calculate the percentage of benzoic acid molecules that are ionized in each solution.
Given: concentrations and pKa
Asked for: percent ionization
Strategy:
A Write both the balanced equilibrium equation for the ionization reaction and the equilibrium equation (Equation 16.15). Use Equation 16.25 to calculate the Ka from the pKa.
B For both the concentrated solution and the dilute solution, use a tabular format to write expressions for the final concentrations of all species in solution. Substitute these values into the equilibrium equation and solve for [C6H5CO2−]f for each solution.
C Use the values of [C6H5CO2−]f and Equation 16.41 to calculate the percent ionization.
Solution:
A If we abbreviate benzoic acid as PhCO2H where Ph = –C6H5, the balanced equilibrium equation for the ionization reaction and the equilibrium equation can be written as follows:
From the pKa, we have Ka = 10−4.20 = 6.3 × 10−5.
B For the more concentrated solution, we set up our table of initial concentrations, changes in concentrations, and final concentrations:
| [PhCO2H] | [H+] | [PhCO2−] | |
|---|---|---|---|
| initial | 0.0500 | 1.00 × 10−7 | 0 |
| change | −x | +x | +x |
| final | (0.0500 − x) | (1.00 × 10−7 + x) | x |
Inserting the expressions for the final concentrations into the equilibrium equation and making our usual assumptions, that [PhCO2−] and [H+] are negligible due to the autoionization of water,
This value is less than 5% of 0.0500, so our simplifying assumption is justified, and [PhCO2−] at equilibrium is 1.8 × 10−3 M. We reach the same conclusion using CHA: KaCHA = (6.3 × 10−5)(0.0500) = 3.2 × 10−6 > 1.0 × 10−6.
C The percent ionized is the ratio of the concentration of PhCO2− to the analytical concentration, multiplied by 100:
Because only 3.6% of the benzoic acid molecules are ionized in a 0.0500 M solution, our simplifying assumptions are confirmed.
B For the more dilute solution, we proceed in exactly the same manner. Our table of concentrations is therefore as follows:
| [PhCO2H] | [H+] | [PhCO2−] | |
|---|---|---|---|
| initial | 0.00500 | 1.00 × 10−7 | 0 |
| change | −x | +x | +x |
| final | (0.00500 − x) | (1.00 × 10−7 + x) | x |
Inserting the expressions for the final concentrations into the equilibrium equation and making our usual simplifying assumptions,
Unfortunately, this number is greater than 10% of 0.00500, so our assumption that the fraction of benzoic acid that is ionized in this solution could be neglected and that (0.00500 − x) ≈ x is not valid. Furthermore, we see that KaCHA = (6.3 × 10−5)(0.00500) = 3.2 × 10−7 < 1.0 × 10−6. Thus the relevant equation is as follows:
which must be solved using the quadratic formula. Multiplying out the quantities,
x2 = (6.3 × 10−5)(0.00500 − x) = (3.2 × 10−7) − (6.3 × 10−5)xRearranging the equation to fit the standard quadratic equation format,
x2 + (6.3 × 10−5)x − (3.2 × 10−7) = 0This equation can be solved by using the quadratic formula:
Because a negative x value corresponds to a negative [PhCO2−], which is not physically meaningful, we use the positive solution: x = 5.3 × 10−4. Thus [PhCO2−] = 5.3 × 10−4 M.
C The percent ionized is therefore
In the more dilute solution (C = 0.00500 M), 11% of the benzoic acid molecules are ionized versus only 3.6% in the more concentrated solution (C = 0.0500 M). Decreasing the analytical concentration by a factor of 10 results in an approximately threefold increase in the percentage of benzoic acid molecules that are ionized.
Exercise
Lactic acid (CH3CH(OH)CO2H) is a weak acid with a pKa of 3.86 at 25°C. What percentage of the lactic acid is ionized in each solution?
Answer:
In Section 16.2 "A Qualitative Description of Acid–Base Equilibriums", you learned how to use Ka and Kb values to qualitatively predict whether reactants or products are favored in an acid–base reaction. Tabulated values of Ka (or pKa) and Kb (or pKb), plus the Kw, enable us to quantitatively determine the direction and extent of reaction for a weak acid and a weak base by calculating K for the reaction. To illustrate how to do this, we begin by writing the dissociation equilibriums for a weak acid and a weak base and then summing them:
Equation 16.48
The overall reaction has H2O on the left and H+ and OH− on the right, which means it involves the autoionization of water in addition to the acid–base equilibrium in which we are interested. We can obtain an equation that includes only the acid–base equilibrium by simply adding the equation for the reverse of the autoionization of water , for which K = 1/Kw, to the overall equilibrium in Equation 16.48 and canceling:
Equation 16.49
Thus the equilibrium constant for the reaction of a weak acid with a weak base is the product of the ionization constants of the acid and the base divided by Kw. Example 10 illustrates how to calculate the equilibrium constant for the reaction of a weak acid with a weak base.
Fish tend to spoil rapidly, even when refrigerated. The cause of the resulting “fishy” odor is a mixture of amines, particularly methylamine (CH3NH2), a volatile weak base (pKb = 3.34). Fish is often served with a wedge of lemon because lemon juice contains citric acid, a triprotic acid with pKa values of 3.13, 4.76, and 6.40 that can neutralize amines. Calculate the equilibrium constant for the reaction of excess citric acid with methylamine, assuming that only the first dissociation constant of citric acid is important.
Given: pKb for base and pKa for acid
Asked for: K
Strategy:
A Write the balanced equilibrium equation and the equilibrium constant expression for the reaction.
B Convert pKa and pKb to Ka and Kb and then use Equation 16.49 to calculate K.
Solution:
A If we abbreviate citric acid as H3citrate, the equilibrium equation for its reaction with methylamine is as follows:
The equilibrium constant expression for this reaction is as follows:
B Equation 16.49 is K = (KaKb)/Kw. Converting pKa and pKb to Ka and Kb gives Ka = 10−3.13 = 7.4 × 10−4 for citric acid and Kb = 10−3.34 = 4.6 × 10−4 for methylamine. Substituting these values into the equilibrium equation,
The value of pK can also be calculated directly by taking the negative logarithm of both sides of Equation 16.49, which gives
pK = pKa + pKb − pKw = 3.13 + 3.34 − 14.00 = −7.53Thus K = 10−(−7.53) = 3.4 × 107, in agreement with the earlier value. In either case, the K values show that the reaction of citric acid with the volatile, foul-smelling methylamine lies very far to the right, favoring the formation of a much less volatile salt with no odor. This is one reason a little lemon juice helps make less-than-fresh fish more appetizing.
Exercise
Dilute aqueous ammonia solution, often used as a cleaning agent, is also effective as a deodorizing agent. To see why, calculate the equilibrium constant for the reaction of aqueous ammonia with butyric acid (CH3CH2CH2CO2H), a particularly foul-smelling substance associated with the odor of rancid butter and smelly socks. The pKb of ammonia is 4.75, and the pKa of butyric acid is 4.83.
Answer: 2.6 × 104
If the concentration of one or more of the species in a solution of an acid or a base is determined experimentally, Ka and Kb can be calculated, and Ka, pKa, Kb, and pKb can be used to quantitatively describe the composition of solutions of acids and bases. The concentrations of all species present in solution can be determined, as can the pH of the solution and the percentage of the acid or base that is ionized. The equilibrium constant for the reaction of a weak acid with a weak base can be calculated from Ka (or pKa), Kb (or pKb), and Kw.
Percent ionization of acid
Percent ionization of base
Equilibrium constant for reaction of a weak acid with a weak base
Explain why the analytical concentration (C) of H2SO4 is equal to [H2SO4] + [HSO4−] + [SO42−].
Write an expression for the analytical concentration (C) of H3PO4 in terms of the concentrations of the species actually present in solution.
For relatively dilute solutions of a weak acid such as acetic acid (CH3CO2H), the concentration of undissociated acetic acid in solution is often assumed to be the same as the analytical concentration. Explain why this is a valid practice.
How does dilution affect the percent ionization of a weak acid or a weak base?
What is the relationship between the Ka of a weak acid and its percent ionization? Does a compound with a large pKa value have a higher or a lower percent ionization than a compound with a small pKa value (assuming the same analytical concentration in both cases)? Explain.
For a dilute solution of a weak acid (HA), show that the pH of the solution can be approximated using the following equation (where CHA is the analytical concentration of the weak acid):
Under what conditions is this approximation valid?
The pKa of NH3 is estimated to be 35. Its conjugate base, the amide ion (NH2−), can be isolated as an alkali metal salt, such as sodium amide (NaNH2). Calculate the pH of a solution prepared by adding 0.100 mol of sodium amide to 1.00 L of water. Does the pH differ appreciably from the pH of a NaOH solution of the same concentration? Why or why not?
Phenol is a topical anesthetic that has been used in throat lozenges to relieve sore throat pain. Describe in detail how you would prepare a 2.00 M solution of phenol (C6H5OH) in water; then write equations to show all the species present in the solution. What is the equilibrium constant expression for the reaction of phenol with water? Use the information in Chapter 27 "Appendix C: Dissociation Constants and p" to calculate the pH of the phenol solution.
Describe in detail how you would prepare a 1.50 M solution of methylamine in water; then write equations to show all the species present in the solution. What is the equilibrium constant expression for the reaction of methylamine with water? Use the information in Table 16.3 "Values of " to calculate the pH of the solution.
A 0.200 M solution of diethylamine, a substance used in insecticides and fungicides, is only 3.9% ionized at 25°C. Write an equation showing the equilibrium reaction and then calculate the pKb of diethylamine. What is the pKa of its conjugate acid, the diethylammonium ion? What is the equilibrium constant expression for the reaction of diethylammonium chloride with water?
A 1.00 M solution of fluoroacetic acid (FCH2CO2H) is 5% dissociated in water. What is the equilibrium constant expression for the dissociation reaction? Calculate the concentration of each species in solution and then calculate the pKa of FCH2CO2H.
The pKa of 3-chlorobutanoic acid (CH3CHClCH2CO2H) is 4.05. What percentage is dissociated in a 1.0 M solution? Do you expect the pKa of butanoic acid to be greater than or less than the pKa of 3-chlorobutanoic acid? Why?
The pKa of the ethylammonium ion (C2H5NH3+) is 10.64. What percentage of ethylamine is ionized in a 1.00 M solution of ethylamine?
The pKa of Cl3CCO2H is 0.64. What is the pH of a 0.580 M solution? What percentage of the Cl3CCO2H is dissociated?
The pH of a 0.150 M solution of aniline hydrochloride (C6H5NH3+Cl−) is 2.70. What is the pKb of the conjugate base, aniline (C6H5NH2)? Do you expect the pKb of (CH3)2CHNH2 to be greater than or less than the pKb of C6H5NH2? Why?
What is the pH of a 0.620 M solution of CH3NH3+Br− if the pKb of CH3NH2 is 10.62?
The pKb of 4-hydroxypyridine is 10.80 at 25°C. What is the pH of a 0.0250 M solution?

The pKa values of formic acid and the methylammonium ion are 3.75 and 10.62, respectively. Calculate K for the following reaction:
The pKa values of butanoic acid and the ammonium ion are 4.82 and 9.24, respectively. Calculate K for the following reaction:
Use the information in Table 16.2 "Values of " to calculate the pH of a 0.0968 M solution of calcium formate.
Calculate the pH of a 0.24 M solution of sodium lactate. The pKa of lactic acid is 3.86.
Use the information in Table 16.3 "Values of " to determine the pH of a solution prepared by dissolving 750.0 mg of methylammonium chloride (CH3NH3+Cl−) in enough water to make 150.0 mL of solution.
Use the information in Table 16.2 "Values of " to determine the pH of a solution prepared by dissolving 855 mg of sodium nitrite (NaNO2) in enough water to make 100.0 mL of solution.
pKb = 9.43; (CH3)2CHNH2 will be a stronger base and have a lower pKb; aniline is a weaker base because the lone pair on the nitrogen atom can be delocalized on the aromatic ring.
3.8 × 10−5
8.18
In Chapter 4 "Reactions in Aqueous Solution", you learned that in an acid–base titration, a buret is used to deliver measured volumes of an acid or a base solution of known concentration (the titrant) to a flask that contains a solution of a base or an acid, respectively, of unknown concentration (the unknown). If the concentration of the titrant is known, then the concentration of the unknown can be determined. The following discussion focuses on the pH changes that occur during an acid–base titration. Plotting the pH of the solution in the flask against the amount of acid or base added produces a titration curveA plot of the pH of the solution being titrated versus the amount of acid or base (of known concentration) added.. The shape of the curve provides important information about what is occurring in solution during the titration.
Part (a) of Figure 16.17 "Solution pH as a Function of the Volume of a Strong Acid or a Strong Base Added to Distilled Water" shows a plot of the pH as 0.20 M HCl is gradually added to 50.00 mL of pure water. The pH of the sample in the flask is initially 7.00 (as expected for pure water), but it drops very rapidly as HCl is added. Eventually the pH becomes constant at 0.70—a point well beyond its value of 1.00 with the addition of 50.0 mL of HCl (0.70 is the pH of 0.20 M HCl). In contrast, when 0.20 M NaOH is added to 50.00 mL of distilled water, the pH (initially 7.00) climbs very rapidly at first but then more gradually, eventually approaching a limit of 13.30 (the pH of 0.20 M NaOH), again well beyond its value of 13.00 with the addition of 50.0 mL of NaOH as shown in part (b) in Figure 16.17 "Solution pH as a Function of the Volume of a Strong Acid or a Strong Base Added to Distilled Water". As you can see from these plots, the titration curve for adding a base is the mirror image of the curve for adding an acid.
Figure 16.17 Solution pH as a Function of the Volume of a Strong Acid or a Strong Base Added to Distilled Water
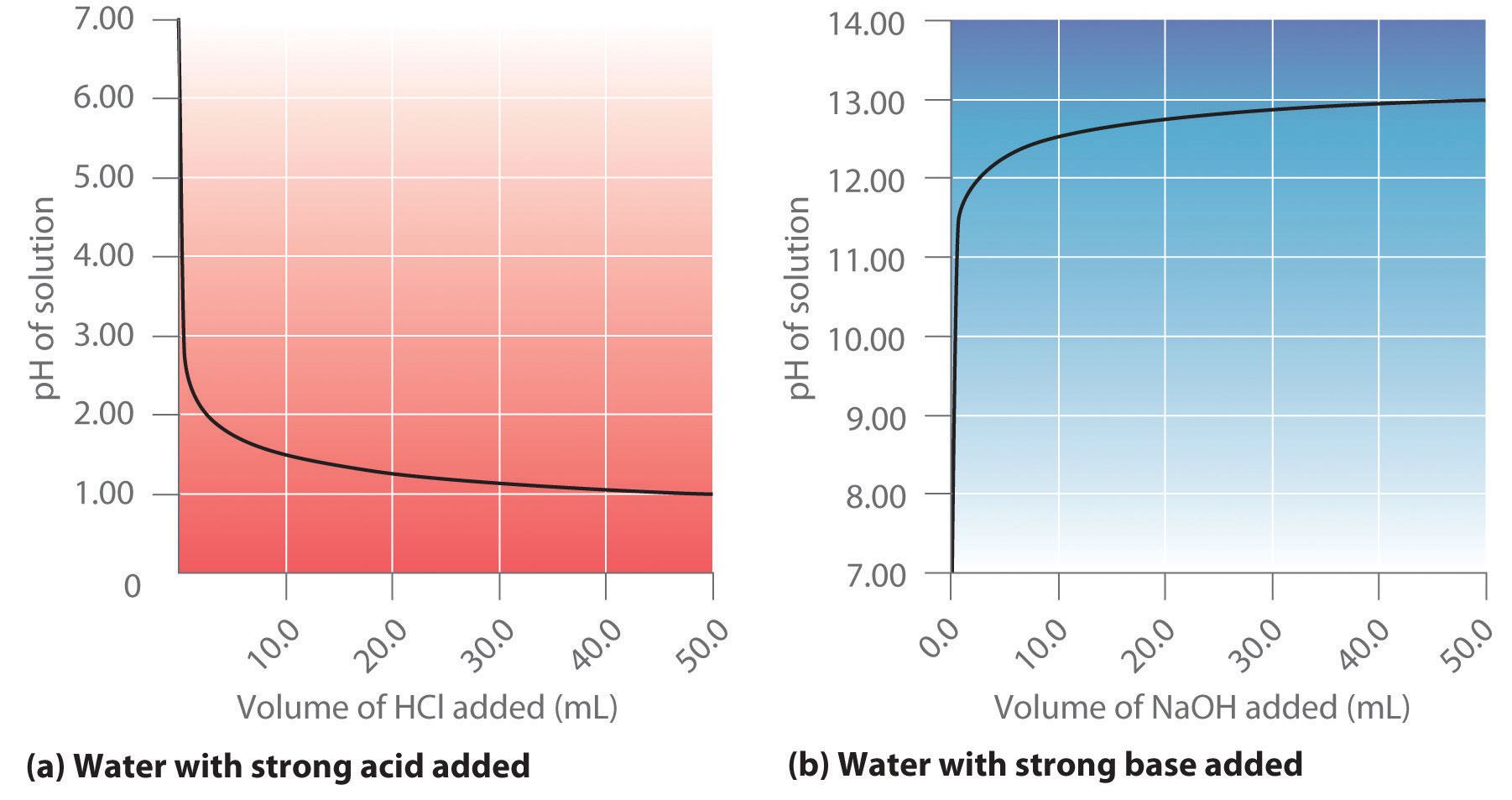
(a) When 0.20 M HCl is added to 50.0 mL of distilled water, the pH rapidly decreases until it reaches a minimum at the pH of 0.20 M HCl. (b) Conversely, when 0.20 M NaOH is added to 50.0 mL of distilled water, the pH rapidly increases until it reaches a maximum at the pH of 0.20 M NaOH.
Suppose that we now add 0.20 M NaOH to 50.0 mL of a 0.10 M solution of HCl. Because HCl is a strong acid that is completely ionized in water, the initial [H+] is 0.10 M, and the initial pH is 1.00. Adding NaOH decreases the concentration of H+ because of the neutralization reaction: (in part (a) in Figure 16.18 "The Titration of (a) a Strong Acid with a Strong Base and (b) a Strong Base with a Strong Acid"). Thus the pH of the solution increases gradually. Near the equivalence pointThe point in a titration where a stoichiometric amount of the titrant has been added., however, the point at which the number of moles of base (or acid) added equals the number of moles of acid (or base) originally present in the solution, the pH increases much more rapidly because most of the H+ ions originally present have been consumed. (For more information on titrations and the equivalence point, see Chapter 4 "Reactions in Aqueous Solution", Section 4.9 "Quantitative Analysis Using Titrations".) For the titration of a monoprotic strong acid (HCl) with a monobasic strong base (NaOH), we can calculate the volume of base needed to reach the equivalence point from the following relationship:
Equation 16.50
If 0.20 M NaOH is added to 50.0 mL of a 0.10 M solution of HCl, we solve for Vb:
Figure 16.18 The Titration of (a) a Strong Acid with a Strong Base and (b) a Strong Base with a Strong Acid
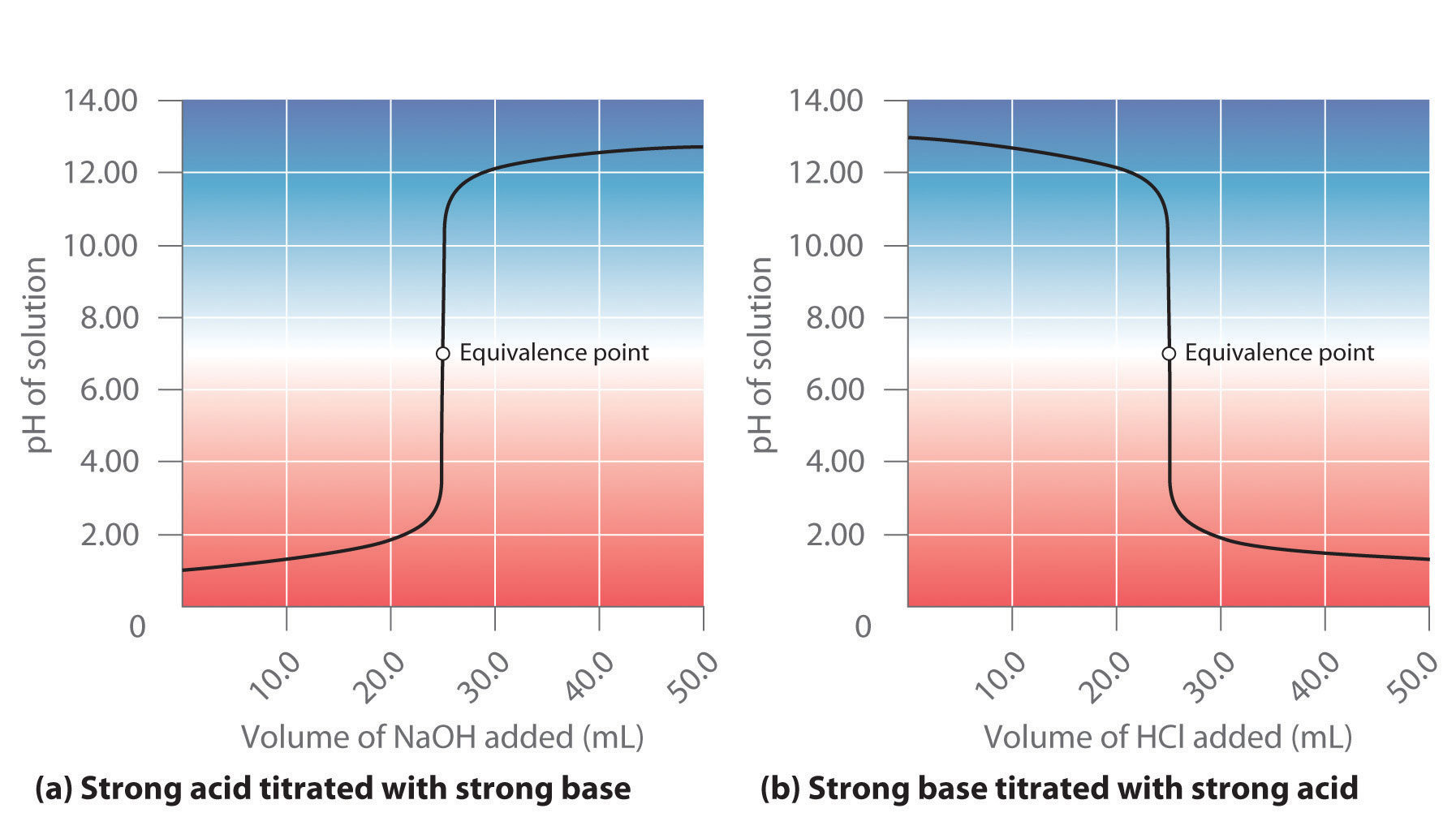
(a) As 0.20 M NaOH is slowly added to 50.0 mL of 0.10 M HCl, the pH increases slowly at first, then increases very rapidly as the equivalence point is approached, and finally increases slowly once more. (b) Conversely, as 0.20 M HCl is slowly added to 50.0 mL of 0.10 M NaOH, the pH decreases slowly at first, then decreases very rapidly as the equivalence point is approached, and finally decreases slowly once more.
At the equivalence point (when 25.0 mL of NaOH solution has been added), the neutralization is complete: only a salt remains in solution (NaCl), and the pH of the solution is 7.00. Adding more NaOH produces a rapid increase in pH, but eventually the pH levels off at a value of about 13.30, the pH of 0.20 M NaOH.
As shown in part (b) in Figure 16.18 "The Titration of (a) a Strong Acid with a Strong Base and (b) a Strong Base with a Strong Acid", the titration of 50.0 mL of a 0.10 M solution of NaOH with 0.20 M HCl produces a titration curve that is nearly the mirror image of the titration curve in part (a) in Figure 16.18 "The Titration of (a) a Strong Acid with a Strong Base and (b) a Strong Base with a Strong Acid". The pH is initially 13.00, and it slowly decreases as HCl is added. As the equivalence point is approached, the pH drops rapidly before leveling off at a value of about 0.70, the pH of 0.20 M HCl.
The titration of either a strong acid with a strong base or a strong base with a strong acid produces an S-shaped curve. The curve is somewhat asymmetrical because the steady increase in the volume of the solution during the titration causes the solution to become more dilute. Due to the leveling effect, the shape of the curve for a titration involving a strong acid and a strong base depends on only the concentrations of the acid and base, not their identities.
The shape of the titration curve involving a strong acid and a strong base depends only on their concentrations, not their identities.
Calculate the pH of the solution after 24.90 mL of 0.200 M NaOH has been added to 50.00 mL of 0.100 M HCl.
Given: volumes and concentrations of strong base and acid
Asked for: pH
Strategy:
A Calculate the number of millimoles of H+ and OH− to determine which, if either, is in excess after the neutralization reaction has occurred. If one species is in excess, calculate the amount that remains after the neutralization reaction.
B Determine the final volume of the solution. Calculate the concentration of the species in excess and convert this value to pH.
Solution:
A Because 0.100 mol/L is equivalent to 0.100 mmol/mL, the number of millimoles of H+ in 50.00 mL of 0.100 M HCl can be calculated as follows:
The number of millimoles of NaOH added is as follows:
Thus H+ is in excess. To completely neutralize the acid requires the addition of 5.00 mmol of OH− to the HCl solution. Because only 4.98 mmol of OH− has been added, the amount of excess H+ is 5.00 mmol − 4.98 mmol = 0.02 mmol of H+.
B The final volume of the solution is 50.00 mL + 24.90 mL = 74.90 mL, so the final concentration of H+ is as follows:
The pH is −log[H+] = −log(3 × 10−4) = 3.5, which is significantly less than the pH of 7.00 for a neutral solution.
Exercise
Calculate the pH of a solution prepared by adding 40.00 mL of 0.237 M HCl to 75.00 mL of a 0.133 M solution of NaOH.
Answer: 11.6
In contrast to strong acids and bases, the shape of the titration curve for a weak acid or a weak base depends dramatically on the identity of the acid or the base and the corresponding Ka or Kb. As we shall see, the pH also changes much more gradually around the equivalence point in the titration of a weak acid or a weak base. As you learned in Section 16.4 "Quantitative Aspects of Acid–Base Equilibriums", [H+] of a solution of a weak acid (HA) is not equal to the concentration of the acid but depends on both its pKa and its concentration. Because only a fraction of a weak acid dissociates, [H+] is less than [HA]. Thus the pH of a solution of a weak acid is greater than the pH of a solution of a strong acid of the same concentration. Part (a) in Figure 16.19 "The Titration of (a) a Weak Acid with a Strong Base and (b) a Weak Base with a Strong Acid" shows the titration curve for 50.0 mL of a 0.100 M solution of acetic acid with 0.200 M NaOH superimposed on the curve for the titration of 0.100 M HCl shown in part (a) in Figure 16.18 "The Titration of (a) a Strong Acid with a Strong Base and (b) a Strong Base with a Strong Acid". Below the equivalence point, the two curves are very different. Before any base is added, the pH of the acetic acid solution is greater than the pH of the HCl solution, and the pH changes more rapidly during the first part of the titration. Note also that the pH of the acetic acid solution at the equivalence point is greater than 7.00. That is, at the equivalence point, the solution is basic. In addition, the change in pH around the equivalence point is only about half as large as for the HCl titration; the magnitude of the pH change at the equivalence point depends on the pKa of the acid being titrated. Above the equivalence point, however, the two curves are identical. Once the acid has been neutralized, the pH of the solution is controlled only by the amount of excess NaOH present, regardless of whether the acid is weak or strong.
The shape of the titration curve of a weak acid or weak base depends heavily on their identities and the Ka or Kb.
The titration curve in part (a) in Figure 16.19 "The Titration of (a) a Weak Acid with a Strong Base and (b) a Weak Base with a Strong Acid" was created by calculating the starting pH of the acetic acid solution before any NaOH is added and then calculating the pH of the solution after adding increasing volumes of NaOH. The procedure is illustrated in the following subsection and Example 12 for three points on the titration curve, using the pKa of acetic acid (4.76 at 25°C; Ka = 1.7 × 10−5).
Figure 16.19 The Titration of (a) a Weak Acid with a Strong Base and (b) a Weak Base with a Strong Acid
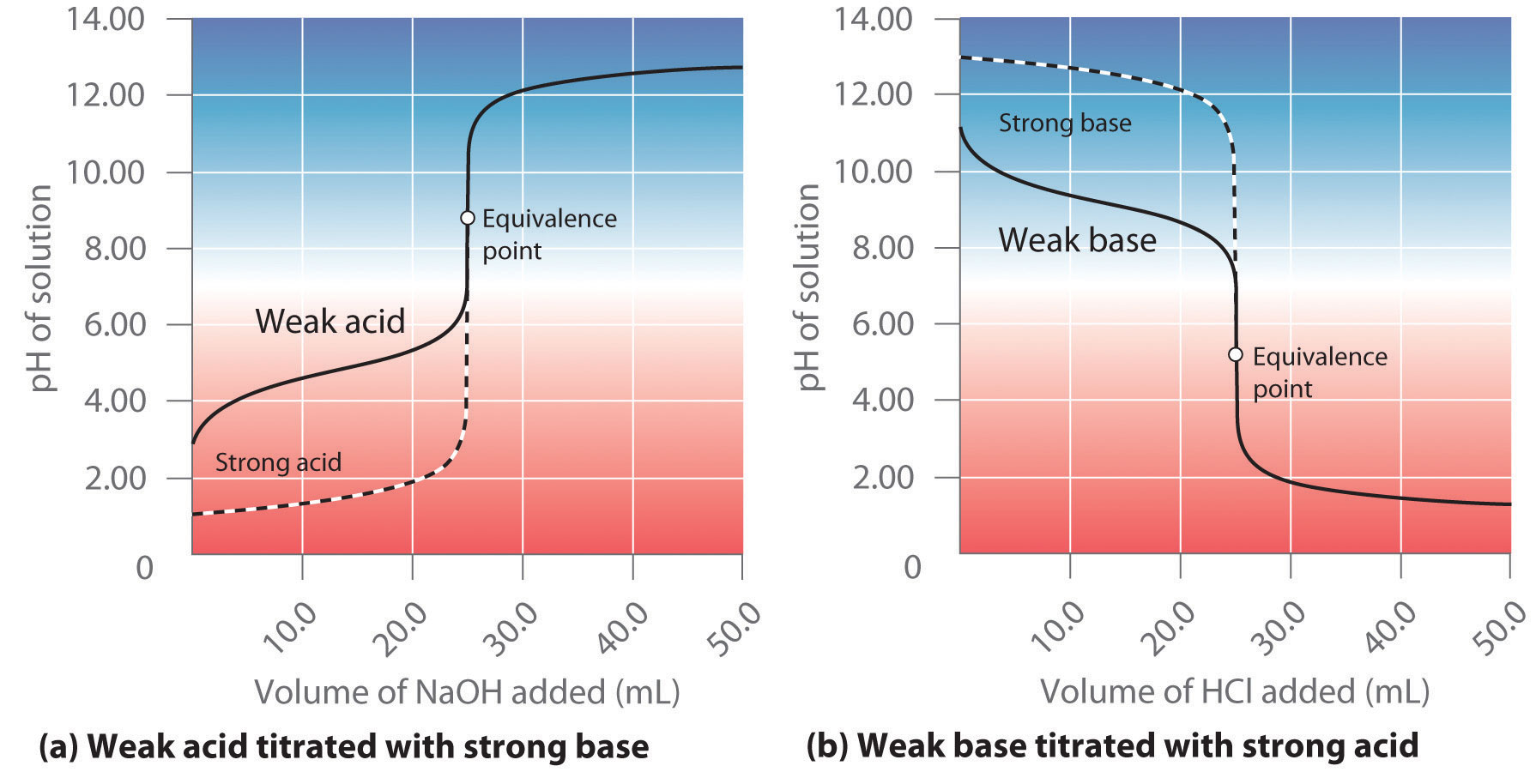
(a) As 0.200 M NaOH is slowly added to 50.0 mL of 0.100 M acetic acid, the pH increases slowly at first, then increases rapidly as the equivalence point is approached, and then again increases more slowly. The corresponding curve for the titration of 50.0 mL of 0.100 M HCl with 0.200 M NaOH is shown as a dashed line. (b) As 0.200 M HCl is slowly added to 50.0 mL of 0.100 M NH3, the pH decreases slowly at first, then decreases rapidly as the equivalence point is approached, and then again decreases more slowly. The corresponding curve for the titration of 50.0 mL of 0.100 M NaOH with 0.200 M HCl is shown as a dashed line.
As explained Section 16.4 "Quantitative Aspects of Acid–Base Equilibriums", if we know Ka or Kb and the initial concentration of a weak acid or a weak base, we can calculate the pH of a solution of a weak acid or a weak base by setting up a table of initial concentrations, changes in concentrations, and final concentrations. In this situation, the initial concentration of acetic acid is 0.100 M. If we define x as [H+] due to the dissociation of the acid, then the table of concentrations for the ionization of 0.100 M acetic acid is as follows:
| [CH3CO2H] | [H+] | [CH3CO2−] | |
|---|---|---|---|
| initial | 0.100 | 1.00 × 10−7 | 0 |
| change | −x | +x | +x |
| final | (0.100 − x) | x | x |
In this and all subsequent examples, we will ignore [H+] and [OH−] due to the autoionization of water when calculating the final concentration. However, you should use Equation 16.45 and Equation 16.46 to check that this assumption is justified.
Inserting the expressions for the final concentrations into the equilibrium equation (and using approximations),
Solving this equation gives x = [H+] = 1.32 × 10−3 M. Thus the pH of a 0.100 M solution of acetic acid is as follows:
pH = −log(1.32 × 10−3) = 2.879Now consider what happens when we add 5.00 mL of 0.200 M NaOH to 50.00 mL of 0.100 M CH3CO2H (part (a) in Figure 16.19 "The Titration of (a) a Weak Acid with a Strong Base and (b) a Weak Base with a Strong Acid"). Because the neutralization reaction proceeds to completion, all of the OH− ions added will react with the acetic acid to generate acetate ion and water:
Equation 16.51
CH3CO2H(aq) + OH−(aq) → CH3CO2−(aq) + H2O(l)All problems of this type must be solved in two steps: a stoichiometric calculation followed by an equilibrium calculation. In the first step, we use the stoichiometry of the neutralization reaction to calculate the amounts of acid and conjugate base present in solution after the neutralization reaction has occurred. In the second step, we use the equilibrium equation (Equation 16.15) to determine [H+] of the resulting solution.
Step 1: To determine the amount of acid and conjugate base in solution after the neutralization reaction, we calculate the amount of CH3CO2H in the original solution and the amount of OH− in the NaOH solution that was added. The acetic acid solution contained
The NaOH solution contained
Comparing the amounts shows that CH3CO2H is in excess. Because OH− reacts with CH3CO2H in a 1:1 stoichiometry, the amount of excess CH3CO2H is as follows:
5.00 mmol CH3CO2H − 1.00 mmol OH− = 4.00 mmol CH3CO2HEach 1 mmol of OH− reacts to produce 1 mmol of acetate ion, so the final amount of CH3CO2− is 1.00 mmol.
The stoichiometry of the reaction is summarized in the following table, which shows the numbers of moles of the various species, not their concentrations.
| [CH3CO2H] | [OH−] | [CH3CO2−] | |
|---|---|---|---|
| initial | 5.00 mmol | 1.00 mmol | 0 mmol |
| change | −1.00 mmol | −1.00 mmol | +1.00 mmol |
| final | 4.00 mmol | 0 mmol | 1.00 mmol |
This table gives the initial amount of acetate and the final amount of OH− ions as 0. Because an aqueous solution of acetic acid always contains at least a small amount of acetate ion in equilibrium with acetic acid, however, the initial acetate concentration is not actually 0. The value can be ignored in this calculation because the amount of CH3CO2− in equilibrium is insignificant compared to the amount of OH− added. Moreover, due to the autoionization of water, no aqueous solution can contain 0 mmol of OH−, but the amount of OH− due to the autoionization of water is insignificant compared to the amount of OH− added. We use the initial amounts of the reactants to determine the stoichiometry of the reaction and defer a consideration of the equilibrium until the second half of the problem.
Step 2: To calculate [H+] at equilibrium following the addition of NaOH, we must first calculate [CH3CO2H] and [CH3CO2−] using the number of millimoles of each and the total volume of the solution at this point in the titration:
Knowing the concentrations of acetic acid and acetate ion at equilibrium and Ka for acetic acid (1.74 × 10−5), we can use Equation 16.15 to calculate [H+] at equilibrium:
Calculating −log[H+] gives pH = −log(6.95 × 10−5) = 4.158.
Comparing the titration curves for HCl and acetic acid in part (a) in Figure 16.19 "The Titration of (a) a Weak Acid with a Strong Base and (b) a Weak Base with a Strong Acid", we see that adding the same amount (5.00 mL) of 0.200 M NaOH to 50 mL of a 0.100 M solution of both acids causes a much smaller pH change for HCl (from 1.00 to 1.14) than for acetic acid (2.88 to 4.16). This is consistent with the qualitative description of the shapes of the titration curves at the beginning of this section. In Example 12, we calculate another point for constructing the titration curve of acetic acid.
What is the pH of the solution after 25.00 mL of 0.200 M NaOH is added to 50.00 mL of 0.100 M acetic acid?
Given: volume and molarity of base and acid
Asked for: pH
Strategy:
A Write the balanced chemical equation for the reaction. Then calculate the initial numbers of millimoles of OH− and CH3CO2H. Determine which species, if either, is present in excess.
B Tabulate the results showing initial numbers, changes, and final numbers of millimoles.
C If excess acetate is present after the reaction with OH−, write the equation for the reaction of acetate with water. Use a tabular format to obtain the concentrations of all the species present.
D Calculate Kb using the relationship Kw = KaKb (Equation 16.23). Calculate [OH−] and use this to calculate the pH of the solution.
Solution:
A Ignoring the spectator ion (Na+), the equation for this reaction is as follows:
CH3CO2H(aq) + OH−(aq) → CH3CO2−(aq) + H2O(l)The initial numbers of millimoles of OH− and CH3CO2H are as follows:
The number of millimoles of OH− equals the number of millimoles of CH3CO2H, so neither species is present in excess.
B Because the number of millimoles of OH− added corresponds to the number of millimoles of acetic acid in solution, this is the equivalence point. The results of the neutralization reaction can be summarized in tabular form.
| [CH3CO2H] | [OH−] | [CH3CO2−] | |
|---|---|---|---|
| initial | 5.00 mmol | 5.00 mmol | 0 mmol |
| change | −5.00 mmol | −5.00 mmol | +5.00 mmol |
| final | 0 mmol | 0 mmol | 5.00 mmol |
C Because the product of the neutralization reaction is a weak base, we must consider the reaction of the weak base with water to calculate [H+] at equilibrium and thus the final pH of the solution. The initial concentration of acetate is obtained from the neutralization reaction:
The equilibrium reaction of acetate with water is as follows:
The equilibrium constant for this reaction is Kb = Kw/Ka, where Ka is the acid ionization constant of acetic acid. We therefore define x as [OH−] produced by the reaction of acetate with water. Here is the completed table of concentrations:
| [CH3CO2−] | [CH3CO2H] | [OH−] | |
|---|---|---|---|
| initial | 0.0667 | 0 | 1.00 × 10−7 |
| change | −x | +x | +x |
| final | (0.0667 − x) | x | x |
D Substituting the expressions for the final values from this table into Equation 16.18,
We can obtain Kb by rearranging Equation 16.23 and substituting the known values:
which we can solve to get x = 6.22 × 10−6. Thus [OH−] = 6.22 × 10−6 M, and the pH of the final solution is 8.794 (part (a) in Figure 16.19 "The Titration of (a) a Weak Acid with a Strong Base and (b) a Weak Base with a Strong Acid"). As expected for the titration of a weak acid, the pH at the equivalence point is greater than 7.00 because the product of the titration is a base, the acetate ion, which then reacts with water to produce OH−.
Exercise
Calculate the pH of a solution prepared by adding 45.0 mL of a 0.213 M HCl solution to 125.0 mL of a 0.150 M solution of ammonia. The pKb of ammonia is 4.75 at 25°C.
Answer: 9.23
As shown in part (b) in Figure 16.19 "The Titration of (a) a Weak Acid with a Strong Base and (b) a Weak Base with a Strong Acid", the titration curve for NH3, a weak base, is the reverse of the titration curve for acetic acid. In particular, the pH at the equivalence point in the titration of a weak base is less than 7.00 because the titration produces an acid.
The identity of the weak acid or weak base being titrated strongly affects the shape of the titration curve. Figure 16.20 "Effect of Acid or Base Strength on the Shape of Titration Curves" illustrates the shape of titration curves as a function of the pKa or the pKb. As the acid or the base being titrated becomes weaker (its pKa or pKb becomes larger), the pH change around the equivalence point decreases significantly. With very dilute solutions, the curve becomes so shallow that it can no longer be used to determine the equivalence point.
Figure 16.20 Effect of Acid or Base Strength on the Shape of Titration Curves
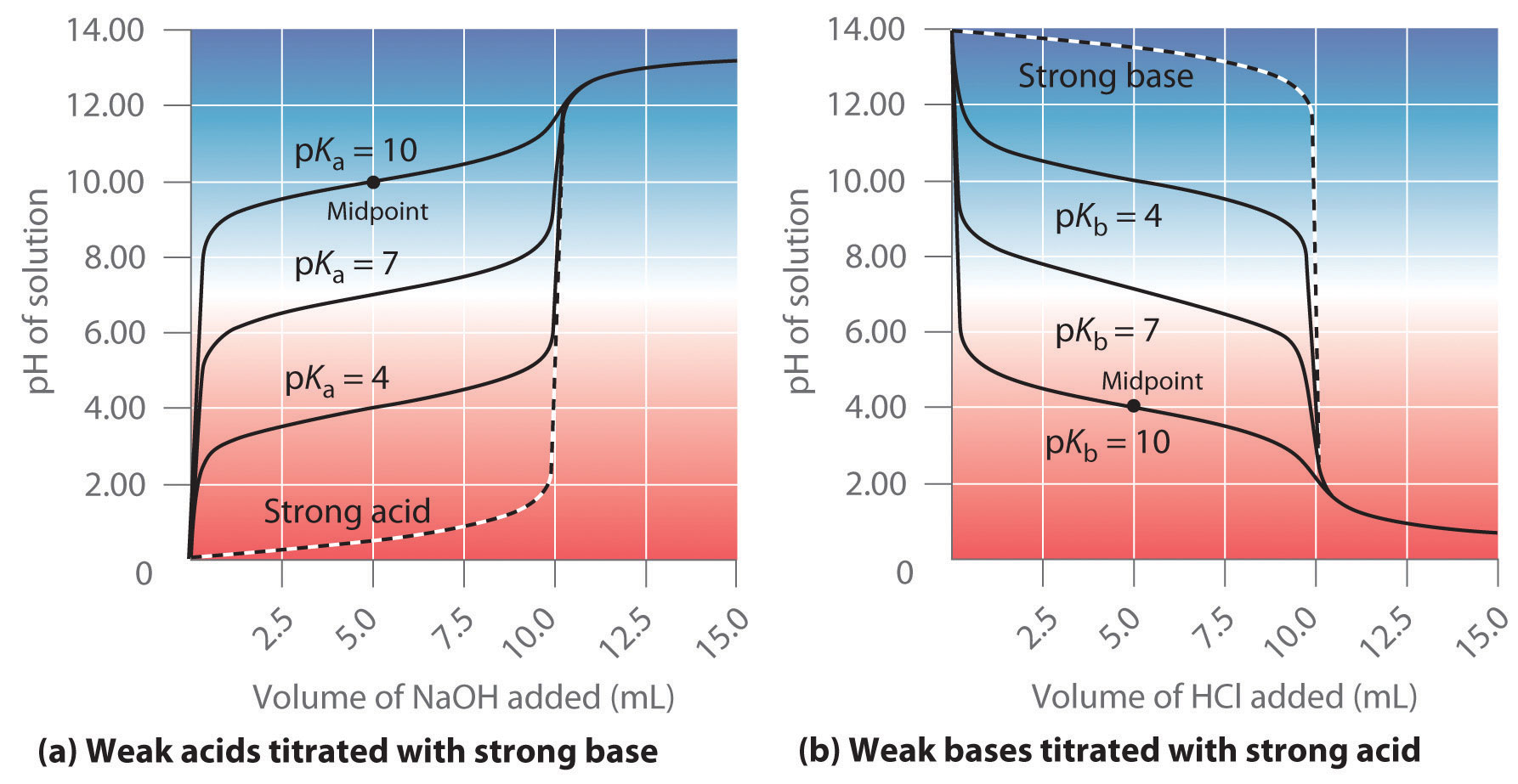
Unlike strong acids or bases, the shape of the titration curve for a weak acid or base depends on the pKa or pKb of the weak acid or base being titrated. (a) Solution pH as a function of the volume of 1.00 M NaOH added to 10.00 mL of 1.00 M solutions of weak acids with the indicated pKa values. (b) Solution pH as a function of the volume of 1.00 M HCl added to 10.00 mL of 1.00 M solutions of weak bases with the indicated pKb values. The shapes of the two sets of curves are essentially identical, but one is flipped vertically in relation to the other. Midpoints are indicated for the titration curves corresponding to pKa = 10 and pKb = 10.
One point in the titration of a weak acid or a weak base is particularly important: the midpointThe point in an acid–base titration at which exactly enough acid (or base) has been added to neutralize one-half of the base (or the acid) originally present: of a titration is defined as the point at which exactly enough acid (or base) has been added to neutralize one-half of the acid (or the base) originally present and occurs halfway to the equivalence point. The midpoint is indicated in part (a) in Figure 16.20 "Effect of Acid or Base Strength on the Shape of Titration Curves" and part (b) in Figure 16.20 "Effect of Acid or Base Strength on the Shape of Titration Curves" for the two shallowest curves. By definition, at the midpoint of the titration of an acid, [HA] = [A−]. Recall from Equation 16.15 that the ionization constant for a weak acid is as follows:
If [HA] = [A−], this reduces to Ka = [H3O+]. Taking the negative logarithm of both sides,
−log Ka = −log[H3O+]From the definitions of pKa and pH, we see that this is identical to
Equation 16.52
pKa = pHThus the pH at the midpoint of the titration of a weak acid is equal to the pKa of the weak acid, as indicated in part (a) in Figure 16.20 "Effect of Acid or Base Strength on the Shape of Titration Curves" for the weakest acid where we see that the midpoint for pKa = 10 occurs at pH = 10. Titration methods can therefore be used to determine both the concentration and the pKa (or the pKb) of a weak acid (or a weak base).
The pH at the midpoint of the titration of a weak acid is equal to the pKa of the weak acid.
When a strong base is added to a solution of a polyprotic acid, the neutralization reaction occurs in stages. The most acidic group is titrated first, followed by the next most acidic, and so forth. If the pKa values are separated by at least three pKa units, then the overall titration curve shows well-resolved “steps” corresponding to the titration of each proton. A titration of the triprotic acid H3PO4 with NaOH is illustrated in Figure 16.21 "Titration Curve for Phosphoric Acid (H" and shows two well-defined steps: the first midpoint corresponds to pKa1, and the second midpoint corresponds to pKa2. Because HPO42− is such a weak acid, pKa3 has such a high value that the third step cannot be resolved using 0.100 M NaOH as the titrant.
Figure 16.21 Titration Curve for Phosphoric Acid (H3PO4), a Typical Polyprotic Acid
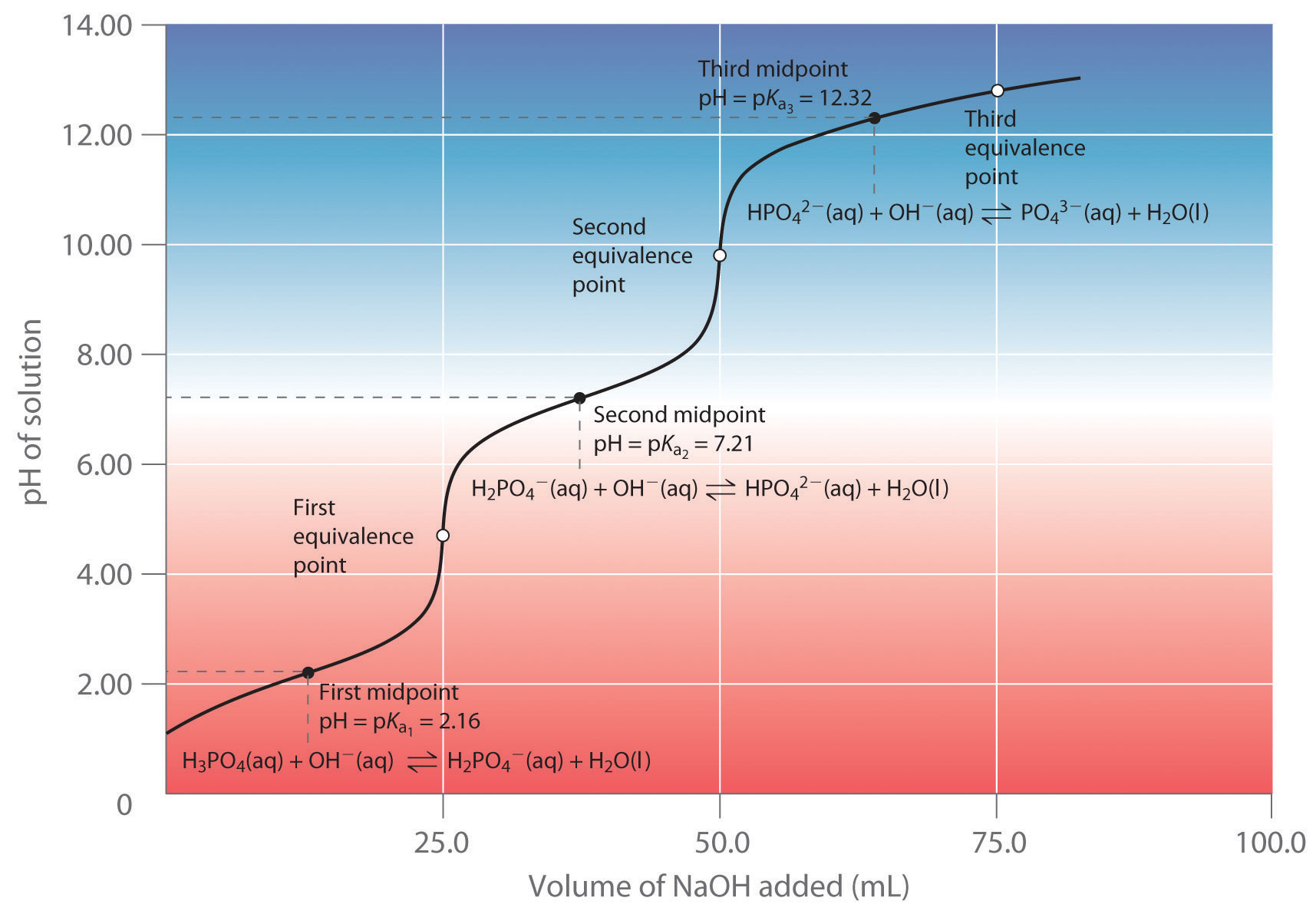
The curve for the titration of 25.0 mL of a 0.100 M H3PO4 solution with 0.100 M NaOH along with the species in solution at each Ka is shown. Note the two distinct equivalence points corresponding to deprotonation of H3PO4 at pH ≈ 4.6 and H2PO42− at pH ≈ 9.8. Because HPO42− is a very weak acid, the third equivalence point, at pH ≈ 13, is not well defined.
The titration curve for the reaction of a polyprotic base with a strong acid is the mirror image of the curve shown in Figure 16.21 "Titration Curve for Phosphoric Acid (H". The initial pH is high, but as acid is added, the pH decreases in steps if the successive pKb values are well separated. Table 16.4 "Values of p" lists the ionization constants and pKa values for some common polyprotic acids and bases.
Calculate the pH of a solution prepared by adding 55.0 mL of a 0.120 M NaOH solution to 100.0 mL of a 0.0510 M solution of oxalic acid (HO2CCO2H), a diprotic acid (abbreviated as H2ox). Oxalic acid, the simplest dicarboxylic acid, is found in rhubarb and many other plants. Rhubarb leaves are toxic because they contain the calcium salt of the fully deprotonated form of oxalic acid, the oxalate ion (−O2CCO2−, abbreviated ox2−).Oxalate salts are toxic for two reasons. First, oxalate salts of divalent cations such as Ca2+ are insoluble at neutral pH but soluble at low pH, as we shall see in Chapter 17 "Solubility and Complexation Equilibriums". As a result, calcium oxalate dissolves in the dilute acid of the stomach, allowing oxalate to be absorbed and transported into cells, where it can react with calcium to form tiny calcium oxalate crystals that damage tissues. Second, oxalate forms stable complexes with metal ions, which can alter the distribution of metal ions in biological fluids.
Given: volume and concentration of acid and base
Asked for: pH
Strategy:
A Calculate the initial millimoles of the acid and the base. Use a tabular format to determine the amounts of all the species in solution.
B Calculate the concentrations of all the species in the final solution. Use Equation 16.16 to determine [H+] and convert this value to pH.
Solution:
A Table 16.4 "Values of p" gives the pKa values of oxalic acid as 1.25 and 3.81. Again we proceed by determining the millimoles of acid and base initially present:
The strongest acid (H2ox) reacts with the base first. This leaves (6.60 − 5.10) = 1.50 mmol of OH− to react with Hox−, forming ox2− and H2O. The reactions can be written as follows:
In tabular form,
| H2ox | OH− | Hox− | ox2− | |
|---|---|---|---|---|
| initial | 5.10 mmol | 6.60 mmol | 0 mmol | 0 mmol |
| change (step 1) | −5.10 mmol | −5.10 mmol | +5.10 mmol | 0 mmol |
| final (step 1) | 0 mmol | 1.50 mmol | 5.10 mmol | 0 mmol |
| change (step 2) | — | −1.50 mmol | −1.50 mmol | +1.50 mmol |
| final | 0 mmol | 0 mmol | 3.60 mmol | 1.50 mmol |
B The equilibrium between the weak acid (Hox−) and its conjugate base (ox2−) in the final solution is determined by the magnitude of the second ionization constant, Ka2 = 10−3.81 = 1.6 × 10−4. To calculate the pH of the solution, we need to know [H+], which is determined using exactly the same method as in the acetic acid titration in Example 12:
final volume of solution = 100.0 mL + 55.0 mL = 155.0 mLThus the concentrations of Hox− and ox2− are as follows:
We can now calculate [H+] at equilibrium using the following equation:
Rearranging this equation and substituting the values for the concentrations of Hox− and ox2−,
So
pH = −log[H+] = −log(3.7 ×10−4) = 3.43This answer makes chemical sense because the pH is between the first and second pKa values of oxalic acid, as it must be. We added enough hydroxide ion to completely titrate the first, more acidic proton (which should give us a pH greater than pKa1), but we added only enough to titrate less than half of the second, less acidic proton, with pKa2. If we had added exactly enough hydroxide to completely titrate the first proton plus half of the second, we would be at the midpoint of the second step in the titration, and the pH would be 3.81, equal to pKa2.
Exercise
Piperazine is a diprotic base used to control intestinal parasites (“worms”) in pets and humans. A dog is given 500 mg (5.80 mmol) of piperazine (pKb1 = 4.27, pKb2 = 8.67). If the dog’s stomach initially contains 100 mL of 0.10 M HCl (pH = 1.00), calculate the pH of the stomach contents after ingestion of the piperazine.
Answer: 4.9
In practice, most acid–base titrations are not monitored by recording the pH as a function of the amount of the strong acid or base solution used as the titrant. Instead, an acid–base indicatorA compound added in small amounts to an acid–base titration to signal the equivalence point by changing color. is often used that, if carefully selected, undergoes a dramatic color change at the pH corresponding to the equivalence point of the titration. Indicators are weak acids or bases that exhibit intense colors that vary with pH. The conjugate acid and conjugate base of a good indicator have very different colors so that they can be distinguished easily. Some indicators are colorless in the conjugate acid form but intensely colored when deprotonated (phenolphthalein, for example), which makes them particularly useful.
We can describe the chemistry of indicators by the following general equation:
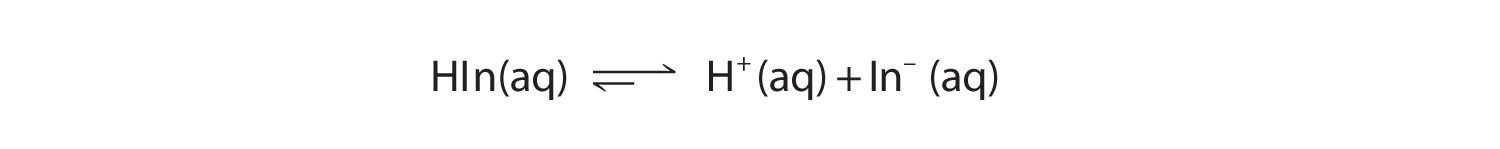
where the protonated form is designated by HIn and the conjugate base by In−. The ionization constant for the deprotonation of indicator HIn is as follows:
Equation 16.53
The pKin (its pKa) determines the pH at which the indicator changes color.
Many different substances can be used as indicators, depending on the particular reaction to be monitored. For example, red cabbage juice contains a mixture of colored substances that change from deep red at low pH to light blue at intermediate pH to yellow at high pH (Figure 16.22 "Naturally Occurring pH Indicators in Red Cabbage Juice"). In all cases, though, a good indicator must have the following properties:
Figure 16.22 Naturally Occurring pH Indicators in Red Cabbage Juice

Red cabbage juice contains a mixture of substances whose color depends on the pH. Each test tube contains a solution of red cabbage juice in water, but the pH of the solutions varies from pH = 2.0 (far left) to pH = 11.0 (far right). At pH = 7.0, the solution is blue.
Synthetic indicators have been developed that meet these criteria and cover virtually the entire pH range. Figure 16.23 "Some Common Acid–Base Indicators" shows the approximate pH range over which some common indicators change color and their change in color. In addition, some indicators (such as thymol blue) are polyprotic acids or bases, which change color twice at widely separated pH values.
Figure 16.23 Some Common Acid–Base Indicators
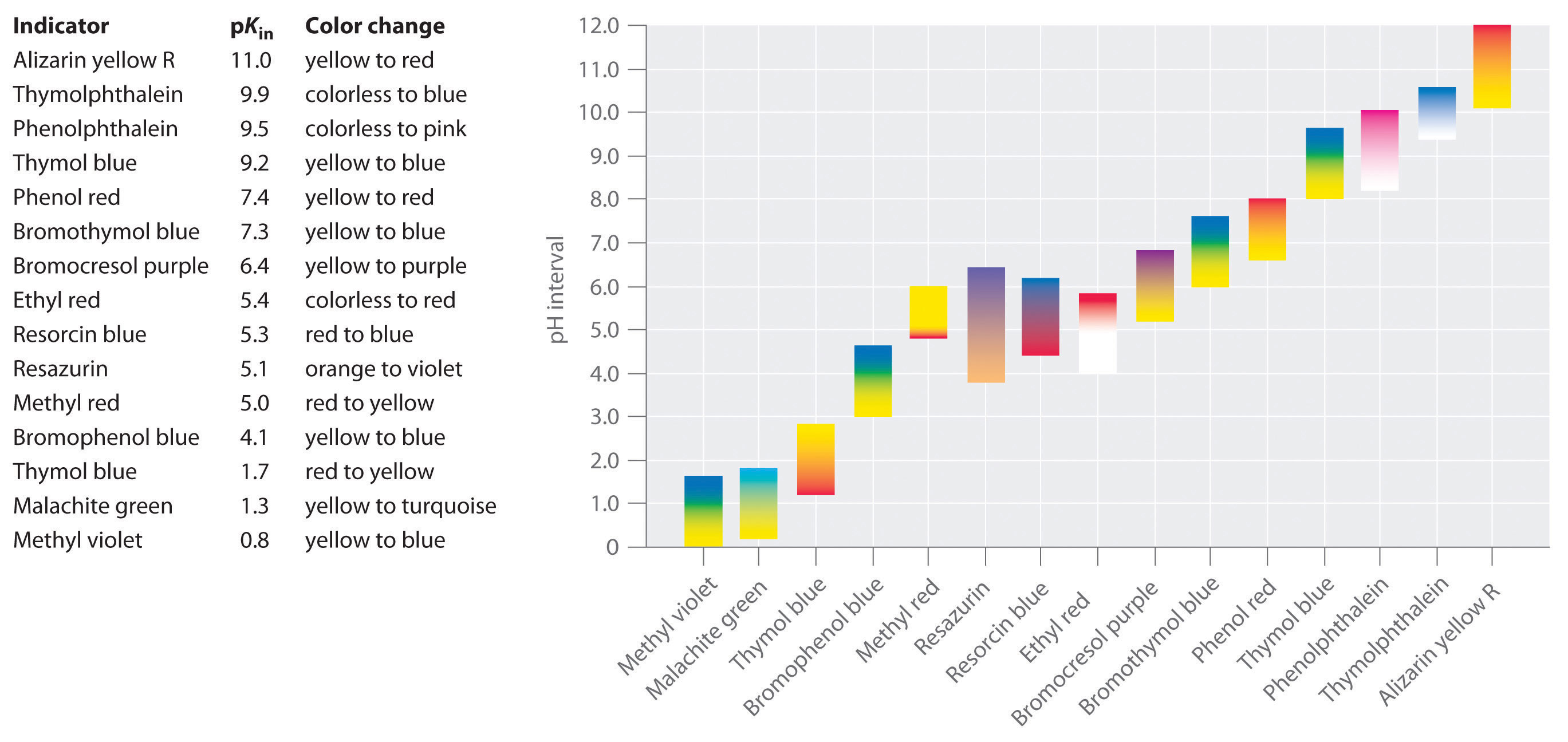
Approximate colors are shown, along with pKin values and the pH range over which the color changes.
It is important to be aware that an indicator does not change color abruptly at a particular pH value; instead, it actually undergoes a pH titration just like any other acid or base. As the concentration of HIn decreases and the concentration of In− increases, the color of the solution slowly changes from the characteristic color of HIn to that of In−. As we will see in Section 16.6 "Buffers", the [In−]/[HIn] ratio changes from 0.1 at a pH one unit below pKin to 10 at a pH one unit above pKin. Thus most indicators change color over a pH range of about two pH units.
We have stated that a good indicator should have a pKin value that is close to the expected pH at the equivalence point. For a strong acid–strong base titration, the choice of the indicator is not especially critical due to the very large change in pH that occurs around the equivalence point. In contrast, using the wrong indicator for a titration of a weak acid or a weak base can result in relatively large errors, as illustrated in Figure 16.24 "Choosing the Correct Indicator for an Acid–Base Titration". This figure shows plots of pH versus volume of base added for the titration of 50.0 mL of a 0.100 M solution of a strong acid (HCl) and a weak acid (acetic acid) with 0.100 M NaOH. The pH ranges over which two common indicators (methyl red, pKin = 5.0, and phenolphthalein, pKin = 9.5) change color are also shown. The horizontal bars indicate the pH ranges over which both indicators change color cross the HCl titration curve, where it is almost vertical. Hence both indicators change color when essentially the same volume of NaOH has been added (about 50 mL), which corresponds to the equivalence point. In contrast, the titration of acetic acid will give very different results depending on whether methyl red or phenolphthalein is used as the indicator. Although the pH range over which phenolphthalein changes color is slightly greater than the pH at the equivalence point of the strong acid titration, the error will be negligible due to the slope of this portion of the titration curve. Just as with the HCl titration, the phenolphthalein indicator will turn pink when about 50 mL of NaOH has been added to the acetic acid solution. In contrast, methyl red begins to change from red to yellow around pH 5, which is near the midpoint of the acetic acid titration, not the equivalence point. Adding only about 25–30 mL of NaOH will therefore cause the methyl red indicator to change color, resulting in a huge error.
Figure 16.24 Choosing the Correct Indicator for an Acid–Base Titration
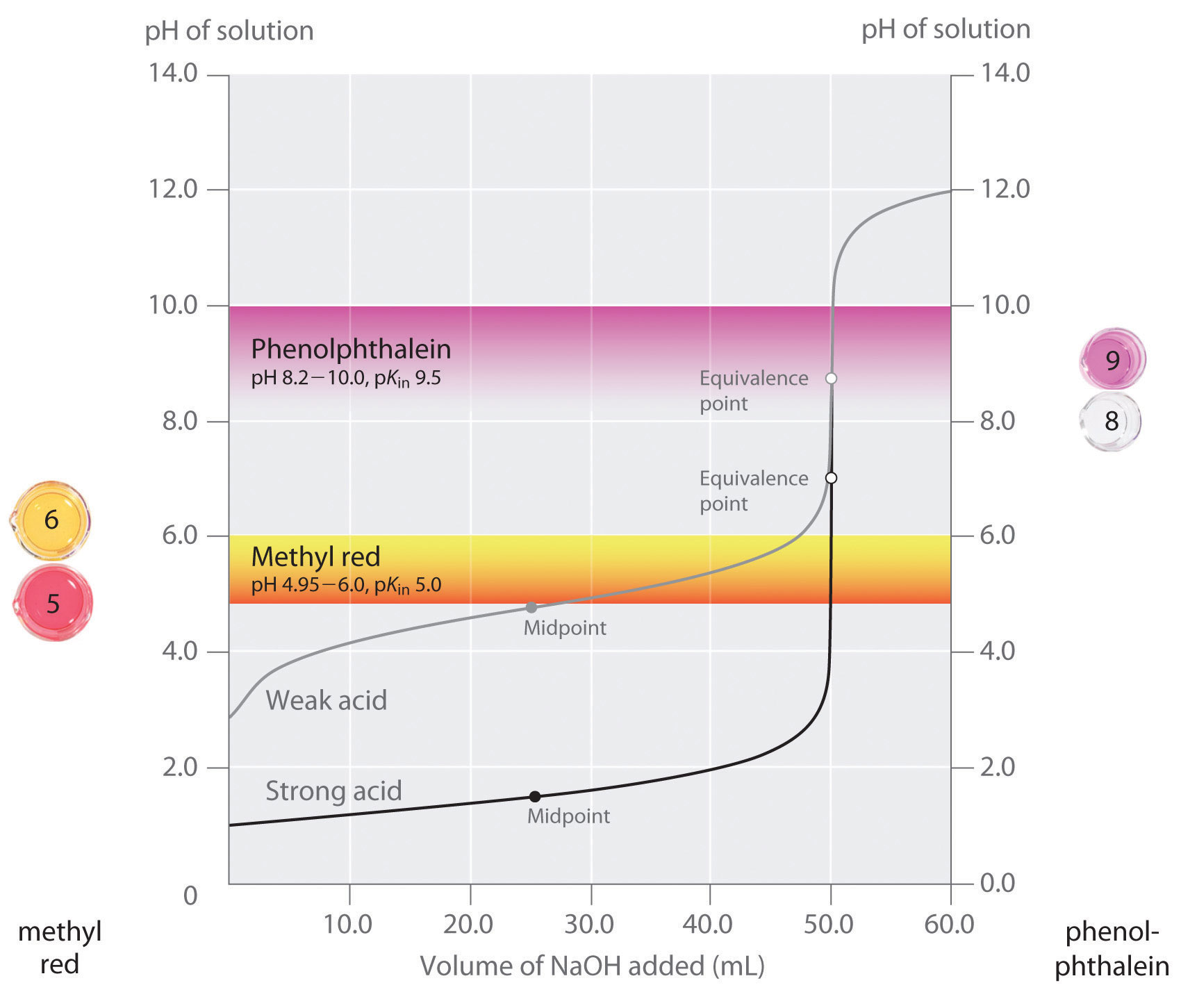
The graph shows the results obtained using two indicators (methyl red and phenolphthalein) for the titration of 0.100 M solutions of a strong acid (HCl) and a weak acid (acetic acid) with 0.100 M NaOH. Due to the steepness of the titration curve of a strong acid around the equivalence point, either indicator will rapidly change color at the equivalence point for the titration of the strong acid. In contrast, the pKin for methyl red (5.0) is very close to the pKa of acetic acid (4.76); the midpoint of the color change for methyl red occurs near the midpoint of the titration, rather than at the equivalence point.
In general, for titrations of strong acids with strong bases (and vice versa), any indicator with a pKin between about 4.0 and 10.0 will do. For the titration of a weak acid, however, the pH at the equivalence point is greater than 7.0, so an indicator such as phenolphthalein or thymol blue, with pKin > 7.0, should be used. Conversely, for the titration of a weak base, where the pH at the equivalence point is less than 7.0, an indicator such as methyl red or bromocresol blue, with pKin < 7.0, should be used.
The existence of many different indicators with different colors and pKin values also provides a convenient way to estimate the pH of a solution without using an expensive electronic pH meter and a fragile pH electrode. Paper or plastic strips impregnated with combinations of indicators are used as “pH paper,” which allows you to estimate the pH of a solution by simply dipping a piece of pH paper into it and comparing the resulting color with the standards printed on the container (Figure 16.25 "pH Paper").
Figure 16.25 pH Paper

pH paper contains a set of indicators that change color at different pH values. The approximate pH of a solution can be determined by simply dipping a paper strip into the solution and comparing the color to the standards provided.
The shape of a titration curve, a plot of pH versus the amount of acid or base added, provides important information about what is occurring in solution during a titration. The shapes of titration curves for weak acids and bases depend dramatically on the identity of the compound. The equivalence point of an acid–base titration is the point at which exactly enough acid or base has been added to react completely with the other component. The equivalence point in the titration of a strong acid or a strong base occurs at pH 7.0. In titrations of weak acids or weak bases, however, the pH at the equivalence point is greater or less than 7.0, respectively. The pH tends to change more slowly before the equivalence point is reached in titrations of weak acids and weak bases than in titrations of strong acids and strong bases. The pH at the midpoint, the point halfway on the titration curve to the equivalence point, is equal to the pKa of the weak acid or the pKb of the weak base. Thus titration methods can be used to determine both the concentration and the pKa (or the pKb) of a weak acid (or a weak base). Acid–base indicators are compounds that change color at a particular pH. They are typically weak acids or bases whose changes in color correspond to deprotonation or protonation of the indicator itself.
Why is the portion of the titration curve that lies below the equivalence point of a solution of a weak acid displaced upward relative to the titration curve of a strong acid? How are the slopes of the curves different at the equivalence point? Why?
Predict whether each solution will be neutral, basic, or acidic at the equivalence point of each titration.
The pKa values of phenol red, bromophenol blue, and phenolphthalein are 7.4, 4.1, and 9.5, respectively. Which indicator is best suited for each acid–base titration?
For the titration of any strong acid with any strong base, the pH at the equivalence point is 7.0. Why is this not usually the case in titrations of weak acids or weak bases?
Why are the titration curves for a strong acid with a strong base and a weak acid with a strong base identical in shape above the equivalence points but not below?
Describe what is occurring on a molecular level during the titration of a weak acid, such as acetic acid, with a strong base, such as NaOH, at the following points along the titration curve. Which of these points corresponds to pH = pKa?
On a molecular level, describe what is happening during the titration of a weak base, such as ammonia, with a strong acid, such as HCl, at the following points along the titration curve. Which of these points corresponds to pOH = pKb?
For the titration of a weak acid with a strong base, use the Ka expression to show that pH = pKa at the midpoint of the titration.
Chemical indicators can be used to monitor pH rapidly and inexpensively. Nevertheless, electronic methods are generally preferred. Why?
Why does adding ammonium chloride to a solution of ammonia in water decrease the pH of the solution?
Given the equilibrium system CH3CO2H(aq) ⇌ CH3CO2−(aq) + H+(aq), explain what happens to the position of the equilibrium and the pH in each case.
Given the equilibrium system CH3NH2(aq) + H2O(l) ⇌ CH3NH3+(aq) + OH−(aq), explain what happens to the position of the equilibrium and the pH in each case.
Calculate the pH of each solution.
What is the pH of a solution prepared by mixing 50.0 mL of 0.225 M HCl with 100.0 mL of a 0.184 M solution of NaOH?
What volume of 0.50 M HCl is needed to completely neutralize 25.00 mL of 0.86 M NaOH?
Calculate the final pH when each pair of solutions is mixed.
Calculate the final pH when each pair of solutions is mixed.
Calcium carbonate is a major contributor to the “hardness” of water. The amount of CaCO3 in a water sample can be determined by titrating the sample with an acid, such as HCl, which produces water and CO2. Write a balanced chemical equation for this reaction. Generate a plot of solution pH versus volume of 0.100 M HCl added for the titration of a solution of 250 mg of CaCO3 in 200.0 mL of water with 0.100 M HCl; assume that the HCl solution is added in 5.00 mL increments. What volume of HCl corresponds to the equivalence point?
For a titration of 50.0 mL of 0.288 M NaOH, you would like to prepare a 0.200 M HCl solution. The only HCl solution available to you, however, is 12.0 M.
While titrating 50.0 mL of a 0.582 M solution of HCl with a solution labeled “0.500 M KOH,” you overshoot the endpoint. To correct the problem, you add 10.00 mL of the HCl solution to your flask and then carefully continue the titration. The total volume of titrant needed for neutralization is 71.9 mL.
Complete the following table and generate a titration curve showing the pH versus volume of added base for the titration of 50.0 mL of 0.288 M HCl with 0.321 M NaOH. Clearly indicate the equivalence point.
| Base Added (mL) | 10.0 | 30.0 | 40.0 | 45.0 | 50.0 | 55.0 | 65.0 | 75.0 |
| pH |
The following data were obtained while titrating 25.0 mL of 0.156 M NaOH with a solution labeled “0.202 M HCl.” Plot the pH versus volume of titrant added. Then determine the equivalence point from your graph and calculate the exact concentration of your HCl solution.
| Volume of HCl (mL) | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| pH | 11.46 | 11.29 | 10.98 | 4.40 | 2.99 | 2.70 | 2.52 |
Fill in the data for the titration of 50.0 mL of 0.241 M formic acid with 0.0982 M KOH. The pKa of formic acid is 3.75. What is the pH of the solution at the equivalence point?
| Volume of Base Added (mL) | 0 | 5 | 10 | 15 | 20 | 25 |
| pH |
Glycine hydrochloride, which contains the fully protonated form of the amino acid glycine, has the following structure:
It is a strong electrolyte that completely dissociates in water. Titration with base gives two equivalence points: the first corresponds to the deprotonation of the carboxylic acid group and the second to loss of the proton from the ammonium group. The corresponding equilibrium equations are as follows:
What is the pH of a solution prepared by adding 38.2 mL of 0.197 M HCl to 150.0 mL of 0.242 M pyridine? The pKb of pyridine is 8.77.
What is the pH of a solution prepared by adding 40.3 mL of 0.289 M NaOH to 150.0 mL of 0.564 M succinic acid (HO2CCH2CH2CO2H)? (For succinic acid, pKa1 = 4.21 and pKa2 = 5.64).
Calculate the pH of a 0.15 M solution of malonic acid (HO2CCH2CO2H), whose pKa values are as follows: pKa1 = 2.85 and pKa2 = 5.70.
43 mL
pH at equivalence point = 8.28
| Volume of Base Added (mL) | 0 | 5 | 10 | 15 | 20 | 25 |
| pH | 2.19 | 2.38 | 2.70 | 2.89 | 3.04 | 3.15 |
1.85
BuffersSolutions that maintain a relatively constant pH when an acid or a base is added. are solutions that maintain a relatively constant pH when an acid or a base is added. They therefore protect, or “buffer,” other molecules in solution from the effects of the added acid or base. Buffers contain either a weak acid (HA) and its conjugate base (A−) or a weak base (B) and its conjugate acid (BH+), and they are critically important for the proper functioning of biological systems. In fact, every biological fluid is buffered to maintain its physiological pH.
To understand how buffers work, let’s look first at how the ionization equilibrium of a weak acid is affected by adding either the conjugate base of the acid or a strong acid (a source of H+). Le Châtelier’s principle can be used to predict the effect on the equilibrium position of the solution.
A typical buffer used in biochemistry laboratories contains acetic acid and a salt such as sodium acetate. Recall that the dissociation reaction of acetic acid is as follows:
Equation 16.54
and the equilibrium constant expression is as follows:
Equation 16.55
Sodium acetate (CH3CO2Na) is a strong electrolyte that ionizes completely in aqueous solution to produce Na+ and CH3CO2− ions. If sodium acetate is added to a solution of acetic acid, Le Châtelier’s principle predicts that the equilibrium in Equation 16.54 will shift to the left, consuming some of the added CH3CO2− and some of the H+ ions originally present in solution:
Because Na+ is a spectator ion, it has no effect on the position of the equilibrium and can be ignored. The addition of sodium acetate produces a new equilibrium composition, in which [H+] is less than the initial value. Because [H+] has decreased, the pH will be higher. Thus adding a salt of the conjugate base to a solution of a weak acid increases the pH. This makes sense because sodium acetate is a base, and adding any base to a solution of a weak acid should increase the pH.
If we instead add a strong acid such as HCl to the system, [H+] increases. Once again the equilibrium is temporarily disturbed, but the excess H+ ions react with the conjugate base (CH3CO2−), whether from the parent acid or sodium acetate, to drive the equilibrium to the left. The net result is a new equilibrium composition that has a lower [CH3CO2−] than before. In both cases, only the equilibrium composition has changed; the ionization constant Ka for acetic acid remains the same. Adding a strong electrolyte that contains one ion in common with a reaction system that is at equilibrium, in this case CH3CO2−, will therefore shift the equilibrium in the direction that reduces the concentration of the common ion. The shift in equilibrium is called the common ion effectThe shift in equilibrium that results when a strong electrolyte containing one ion in common with a reaction system that is at equilibrium is added to the system..
Adding a common ion to a system at equilibrium affects the equilibrium composition but not the ionization constant.
In Section 16.4 "Quantitative Aspects of Acid–Base Equilibriums", we calculated that a 0.150 M solution of formic acid at 25°C (pKa = 3.75) has a pH of 2.28 and is 3.5% ionized.
Given: solution concentration and pH, pKa, and percent ionization of acid; final concentration of conjugate base or strong acid added
Asked for: pH and percent ionization of formic acid
Strategy:
A Write a balanced equilibrium equation for the ionization equilibrium of formic acid. Tabulate the initial concentrations, the changes, and the final concentrations.
B Substitute the expressions for the final concentrations into the expression for Ka. Calculate [H+] and the pH of the solution.
C Construct a table of concentrations for the dissociation of formic acid. To determine the percent ionization, determine the anion concentration, divide it by the initial concentration of formic acid, and multiply the result by 100.
Solution:
A Because sodium formate is a strong electrolyte, it ionizes completely in solution to give formate and sodium ions. The Na+ ions are spectator ions, so they can be ignored in the equilibrium equation. Because water is both a much weaker acid than formic acid and a much weaker base than formate, the acid–base properties of the solution are determined solely by the formic acid ionization equilibrium:
The initial concentrations, the changes in concentration that occur as equilibrium is reached, and the final concentrations can be tabulated.
| [HCO2H] | [H+] | [HCO2−] | |
|---|---|---|---|
| initial | 0.150 | 1.00 × 10−7 | 0.100 |
| change | −x | +x | +x |
| final | (0.150 − x) | x | (0.100 + x) |
B We substitute the expressions for the final concentrations into the equilibrium constant expression and make our usual simplifying assumptions, so
Rearranging and solving for x,
The value of x is small compared with 0.150 or 0.100 M, so our assumption about the extent of ionization is justified. Moreover, KaCHA = (1.8 × 10−4)(0.150) = 2.7 × 10−5, which is greater than 1.0 × 10−6, so again, our assumption is justified. The final pH is −log(2.7 × 10−4) = 3.57, compared with the initial value of 2.29. Thus adding a salt containing the conjugate base of the acid has increased the pH of the solution, as we expect based on Le Châtelier’s principle; the stress on the system has been relieved by the consumption of H+ ions, driving the equilibrium to the left.
C Because HCl is a strong acid, it ionizes completely, and chloride is a spectator ion that can be neglected. Thus the only relevant acid–base equilibrium is again the dissociation of formic acid, and initially the concentration of formate is zero. We can construct a table of initial concentrations, changes in concentration, and final concentrations.
| [HCO2H] | [H+] | [HCO2−] | |
|---|---|---|---|
| initial | 0.150 | 0.200 | 0 |
| change | −x | +x | +x |
| final | (0.150 − x) | (0.200 + x) | x |
To calculate the percentage of formic acid that is ionized under these conditions, we have to determine the final [HCO2−]. We substitute final concentrations into the equilibrium constant expression and make the usual simplifying assumptions, so
Rearranging and solving for x,
Once again, our simplifying assumptions are justified. The percent ionization of formic acid is as follows:
Adding the strong acid to the solution, as shown in the table, decreased the percent ionization of formic acid by a factor of approximately 38 (3.45%/0.0900%). Again, this is consistent with Le Châtelier’s principle: adding H+ ions drives the dissociation equlibrium to the left.
Exercise
As you learned in Example 8, a 0.225 M solution of ethylamine (CH3CH2NH2, pKb = 3.19) has a pH of 12.08 and a percent ionization of 5.4% at 20°C. Calculate the following:
Answer:
Now let’s suppose we have a buffer solution that contains equimolar concentrations of a weak base (B) and its conjugate acid (BH+). The general equation for the ionization of a weak base is as follows:
Equation 16.56
If the equilibrium constant for the reaction as written in Equation 16.56 is small, for example Kb = 10−5, then the equilibrium constant for the reverse reaction is very large: K = 1/Kb = 105. Adding a strong base such as OH− to the solution therefore causes the equilibrium in Equation 16.56 to shift to the left, consuming the added OH−. As a result, the OH− ion concentration in solution remains relatively constant, and the pH of the solution changes very little. Le Châtelier’s principle predicts the same outcome: when the system is stressed by an increase in the OH− ion concentration, the reaction will proceed to the left to counteract the stress.
If the pKb of the base is 5.0, the pKa of its conjugate acid is pKa = pKw − pKb = 14.0 – 5.0 = 9.0. Thus the equilibrium constant for ionization of the conjugate acid is even smaller than that for ionization of the base. The ionization reaction for the conjugate acid of a weak base is written as follows:
Equation 16.57
Again, the equilibrium constant for the reverse of this reaction is very large: K = 1/Ka = 109. If a strong acid is added, it is neutralized by reaction with the base as the reaction in Equation 16.57 shifts to the left. As a result, the H+ ion concentration does not increase very much, and the pH changes only slightly. In effect, a buffer solution behaves somewhat like a sponge that can absorb H+ and OH− ions, thereby preventing large changes in pH when appreciable amounts of strong acid or base are added to a solution.
Buffers are characterized by the pH range over which they can maintain a more or less constant pH and by their buffer capacityThe amount of strong acid or strong base that a buffer solution can absorb before the pH changes dramatically., the amount of strong acid or base that can be absorbed before the pH changes significantly. Although the useful pH range of a buffer depends strongly on the chemical properties of the weak acid and weak base used to prepare the buffer (i.e., on K), its buffer capacity depends solely on the concentrations of the species in the buffered solution. The more concentrated the buffer solution, the greater its buffer capacity. As illustrated in Figure 16.26 "Effect of Buffer Concentration on the Capacity of a Buffer", when NaOH is added to solutions that contain different concentrations of an acetic acid/sodium acetate buffer, the observed change in the pH of the buffer is inversely proportional to the concentration of the buffer. If the buffer capacity is 10 times larger, then the buffer solution can absorb 10 times more strong acid or base before undergoing a significant change in pH.
Figure 16.26 Effect of Buffer Concentration on the Capacity of a Buffer
A buffer maintains a relatively constant pH when acid or base is added to a solution. The addition of even tiny volumes of 0.10 M NaOH to 100.0 mL of distilled water results in a very large change in pH. As the concentration of a 50:50 mixture of sodium acetate/acetic acid buffer in the solution is increased from 0.010 M to 1.00 M, the change in the pH produced by the addition of the same volume of NaOH solution decreases steadily. For buffer concentrations of at least 0.500 M, the addition of even 25 mL of the NaOH solution results in only a relatively small change in pH.
The pH of a buffer can be calculated from the concentrations of the weak acid and the weak base used to prepare it, the concentration of the conjugate base and conjugate acid, and the pKa or pKb of the weak acid or weak base. The procedure is analogous to that used in Example 14 to calculate the pH of a solution containing known concentrations of formic acid and formate.
An alternative method frequently used to calculate the pH of a buffer solution is based on a rearrangement of the equilibrium equation for the dissociation of a weak acid. The simplified ionization reaction is for which the equilibrium constant expression is as follows:
Equation 16.58
This equation can be rearranged as follows:
Equation 16.59
Taking the logarithm of both sides and multiplying both sides by −1,
Equation 16.60
Replacing the negative logarithms in Equation 16.60,
Equation 16.61
or, more generally,
Equation 16.62
Equation 16.61 and Equation 16.62 are both forms of the Henderson-Hasselbalch equationA rearranged version of the equilibrium constant expression that provides a direct way to calculate the pH of a buffer solution: pH = + log([base]/[acid])., named after the two early-20th-century chemists who first noticed that this rearranged version of the equilibrium constant expression provides an easy way to calculate the pH of a buffer solution. In general, the validity of the Henderson-Hasselbalch equation may be limited to solutions whose concentrations are at least 100 times greater than their Ka values.
There are three special cases where the Henderson-Hasselbalch equation is easily interpreted without the need for calculations:
Each time we increase the [base]/[acid] ratio by 10, the pH of the solution increases by 1 pH unit. Conversely, if the [base]/[acid] ratio is 0.1, then pH = pKa − 1. Each additional factor-of-10 decrease in the [base]/[acid] ratio causes the pH to decrease by 1 pH unit.
If [base] = [acid] for a buffer, then pH = pKa. Changing this ratio by a factor of 10 either way changes the pH by ±1 unit.
What is the pH of a solution that contains
Given: concentration of acid, conjugate base, and pKa; concentration of base, conjugate acid, and pKb
Asked for: pH
Strategy:
Substitute values into either form of the Henderson-Hasselbalch equation (Equation 16.61 or Equation 16.62) to calculate the pH.
Solution:
According to the Henderson-Hasselbalch equation, the pH of a solution that contains both a weak acid and its conjugate base is pH = pKa + log([A−]/[HA]). Inserting the given values into the equation,
This result makes sense because the [A−]/[HA] ratio is between 1 and 10, so the pH of the buffer must be between the pKa (3.75) and pKa + 1, or 4.75.
This is identical to part (a), except for the concentrations of the acid and the conjugate base, which are 10 times lower. Inserting the concentrations into the Henderson-Hasselbalch equation,
This result is identical to the result in part (a), which emphasizes the point that the pH of a buffer depends only on the ratio of the concentrations of the conjugate base and the acid, not on the magnitude of the concentrations. Because the [A−]/[HA] ratio is the same as in part (a), the pH of the buffer must also be the same (3.95).
In this case, we have a weak base, pyridine (Py), and its conjugate acid, the pyridinium ion (HPy+). We will therefore use Equation 16.62, the more general form of the Henderson-Hasselbalch equation, in which “base” and “acid” refer to the appropriate species of the conjugate acid–base pair. We are given [base] = [Py] = 0.119 M and [acid] = [HPy+] = 0.234 M. We also are given pKb = 8.77 for pyridine, but we need pKa for the pyridinium ion. Recall from Equation 16.23 that the pKb of a weak base and the pKa of its conjugate acid are related: pKa + pKb = pKw. Thus pKa for the pyridinium ion is pKw − pKb = 14.00 − 8.77 = 5.23. Substituting this pKa value into the Henderson-Hasselbalch equation,
Once again, this result makes sense: the [B]/[BH+] ratio is about 1/2, which is between 1 and 0.1, so the final pH must be between the pKa (5.23) and pKa − 1, or 4.23.
Exercise
What is the pH of a solution that contains
The pKa of benzoic acid is 4.20, and the pKb of trimethylamine is also 4.20.
Answer:
The Henderson-Hasselbalch equation can also be used to calculate the pH of a buffer solution after adding a given amount of strong acid or strong base, as demonstrated in Example 16.
The buffer solution in Example 15 contained 0.135 M HCO2H and 0.215 M HCO2Na and had a pH of 3.95.
Given: composition and pH of buffer; concentration and volume of added acid or base
Asked for: final pH
Strategy:
A Calculate the amounts of formic acid and formate present in the buffer solution using the procedure from Example 14. Then calculate the amount of acid or base added.
B Construct a table showing the amounts of all species after the neutralization reaction. Use the final volume of the solution to calculate the concentrations of all species. Finally, substitute the appropriate values into the Henderson-Hasselbalch equation (Equation 16.62) to obtain the pH.
Solution:
The added HCl (a strong acid) or NaOH (a strong base) will react completely with formate (a weak base) or formic acid (a weak acid), respectively, to give formic acid or formate and water. We must therefore calculate the amounts of formic acid and formate present after the neutralization reaction.
A We begin by calculating the millimoles of formic acid and formate present in 100 mL of the initial pH 3.95 buffer:
The millimoles of H+ in 5.00 mL of 1.00 M HCl is as follows:
B Next, we construct a table of initial amounts, changes in amounts, and final amounts:
| HCO2−(aq) + H+(aq) → HCO2H(aq) | |||
|---|---|---|---|
| [HCO2−] | [H+] | [HCO2H] | |
| initial | 21.5 mmol | 5.00 mmol | 13.5 mmol |
| change | −5.00 mmol | −5.00 mmol | +5.00 mmol |
| final | 16.5 mmol | ∼0 mmol | 18.5 mmol |
The final amount of H+ in solution is given as “∼0 mmol.” For the purposes of the stoichiometry calculation, this is essentially true, but remember that the point of the problem is to calculate the final [H+] and thus the pH. We now have all the information we need to calculate the pH. We can use either the lengthy procedure of Example 14 or the Henderson–Hasselbach equation. Because we have performed many equilibrium calculations in this chapter, we’ll take the latter approach. The Henderson-Hasselbalch equation requires the concentrations of HCO2− and HCO2H, which can be calculated using the number of millimoles (n) of each and the total volume (VT). Substituting these values into the Henderson-Hasselbalch equation,
Because the total volume appears in both the numerator and denominator, it cancels. We therefore need to use only the ratio of the number of millimoles of the conjugate base to the number of millimoles of the weak acid. So
Once again, this result makes sense on two levels. First, the addition of HCl has decreased the pH from 3.95, as expected. Second, the ratio of HCO2− to HCO2H is slightly less than 1, so the pH should be between the pKa and pKa − 1.
A The procedure for solving this part of the problem is exactly the same as that used in part (a). We have already calculated the numbers of millimoles of formic acid and formate in 100 mL of the initial pH 3.95 buffer: 13.5 mmol of HCO2H and 21.5 mmol of HCO2−. The number of millimoles of OH− in 5.00 mL of 1.00 M NaOH is as follows:
B With this information, we can construct a table of initial amounts, changes in amounts, and final amounts.
| HCO2H(aq) + OH−(aq) → HCO2−(aq) + H2O(l) | |||
|---|---|---|---|
| [HCO2H] | [OH−] | [HCO2−] | |
| initial | 13.5 mmol | 5.00 mmol | 21.5 mmol |
| change | −5.00 mmol | −5.00 mmol | +5.00 mmol |
| final | 8.5 mmol | ∼0 mmol | 26.5 mmol |
The final amount of OH− in solution is not actually zero; this is only approximately true based on the stoichiometric calculation. We can calculate the final pH by inserting the numbers of millimoles of both HCO2− and HCO2H into the simplified Henderson-Hasselbalch expression used in part (a) because the volume cancels:
Once again, this result makes chemical sense: the pH has increased, as would be expected after adding a strong base, and the final pH is between the pKa and pKa + 1, as expected for a solution with a HCO2−/HCO2H ratio between 1 and 10.
Exercise
The buffer solution from Example 15 contained 0.119 M pyridine and 0.234 M pyridine hydrochloride and had a pH of 4.94.
Answer:
Only the amounts (in moles or millimoles) of the acidic and basic components of the buffer are needed to use the Henderson-Hasselbalch equation, not their concentrations.
The most effective buffers contain equal concentrations of an acid and its conjugate base.
The results obtained in Example 16 and its corresponding exercise demonstrate how little the pH of a well-chosen buffer solution changes despite the addition of a significant quantity of strong acid or strong base. Suppose we had added the same amount of HCl or NaOH solution to 100 mL of an unbuffered solution at pH 3.95 (corresponding to 1.1 × 10−4 M HCl). In this case, adding 5.00 mL of 1.00 M HCl would lower the final pH to 1.32 instead of 3.70, whereas adding 5.00 mL of 1.00 M NaOH would raise the final pH to 12.68 rather than 4.24. (Try verifying these values by doing the calculations yourself.) Thus the presence of a buffer significantly increases the ability of a solution to maintain an almost constant pH.
A buffer that contains approximately equal amounts of a weak acid and its conjugate base in solution is equally effective at neutralizing either added base or added acid. This is shown in Figure 16.27 "Distribution Curve Showing the Fraction of Acetic Acid Molecules and Acetate Ions as a Function of pH in a Solution of Acetic Acid" for an acetic acid/sodium acetate buffer. Adding a given amount of strong acid shifts the system along the horizontal axis to the left, whereas adding the same amount of strong base shifts the system the same distance to the right. In either case, the change in the ratio of CH3CO2− to CH3CO2H from 1:1 reduces the buffer capacity of the solution.
Figure 16.27 Distribution Curve Showing the Fraction of Acetic Acid Molecules and Acetate Ions as a Function of pH in a Solution of Acetic Acid
The pH range over which the acetic acid/sodium acetate system is an effective buffer (the darker shaded region) corresponds to the region in which appreciable concentrations of both species are present (pH 3.76–5.76, corresponding to pH = pKa ± 1).
There is a strong correlation between the effectiveness of a buffer solution and the titration curves discussed in Section 16.5 "Acid–Base Titrations". Consider the schematic titration curve of a weak acid with a strong base shown in Figure 16.28 "The Relationship between Titration Curves and Buffers". As indicated by the labels, the region around pKa corresponds to the midpoint of the titration, when approximately half the weak acid has been neutralized. This portion of the titration curve corresponds to a buffer: it exhibits the smallest change in pH per increment of added strong base, as shown by the nearly horizontal nature of the curve in this region. The nearly flat portion of the curve extends only from approximately a pH value of 1 unit less than the pKa to approximately a pH value of 1 unit greater than the pKa, which is why buffer solutions usually have a pH that is within ±1 pH units of the pKa of the acid component of the buffer.
Figure 16.28 The Relationship between Titration Curves and Buffers
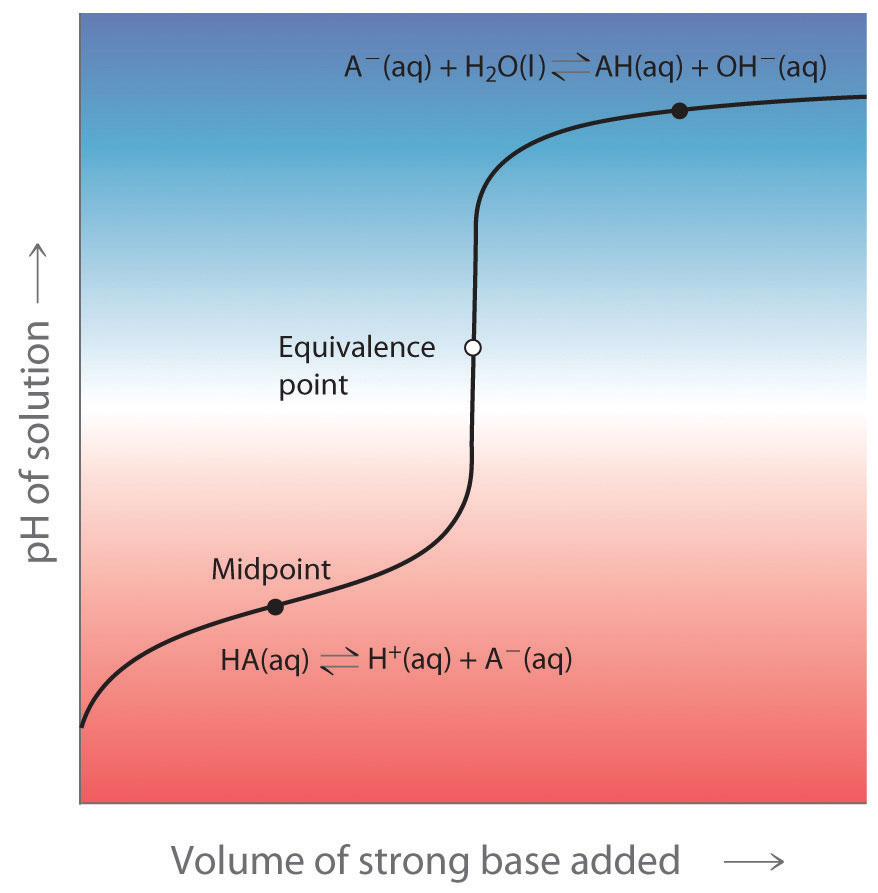
This schematic plot of pH for the titration of a weak acid with a strong base shows the nearly flat region of the titration curve around the midpoint, which corresponds to the formation of a buffer. At the lower left, the pH of the solution is determined by the equilibrium for dissociation of the weak acid; at the upper right, the pH is determined by the equilibrium for reaction of the conjugate base with water.
In the region of the titration curve at the lower left, before the midpoint, the acid–base properties of the solution are dominated by the equilibrium for dissociation of the weak acid, corresponding to Ka. In the region of the titration curve at the upper right, after the midpoint, the acid–base properties of the solution are dominated by the equilibrium for reaction of the conjugate base of the weak acid with water, corresponding to Kb. However, we can calculate either Ka or Kb from the other because they are related by Kw.
Metabolic processes produce large amounts of acids and bases, yet organisms are able to maintain an almost constant internal pH because their fluids contain buffers. This is not to say that the pH is uniform throughout all cells and tissues of a mammal. The internal pH of a red blood cell is about 7.2, but the pH of most other kinds of cells is lower, around 7.0. Even within a single cell, different compartments can have very different pH values. For example, one intracellular compartment in white blood cells has a pH of around 5.0.
Because no single buffer system can effectively maintain a constant pH value over the entire physiological range of approximately pH 5.0 to 7.4, biochemical systems use a set of buffers with overlapping ranges. The most important of these is the CO2/HCO3− system, which dominates the buffering action of blood plasma.
The acid–base equilibrium in the CO2/HCO3− buffer system is usually written as follows:
Equation 16.63
with Ka = 4.5 × 10−7 and pKa = 6.35 at 25°C. In fact, Equation 16.63 is a grossly oversimplified version of the CO2/HCO3− system because a solution of CO2 in water contains only rather small amounts of H2CO3. Thus Equation 16.63 does not allow us to understand how blood is actually buffered, particularly at a physiological temperature of 37°C. As shown in Equation 16.64, CO2 is in equilibrium with H2CO3, but the equilibrium lies far to the left, with an H2CO3/CO2 ratio less than 0.01 under most conditions:
Equation 16.64
with K′ = 4.0 × 10−3 at 37°C. The true pKa of carbonic acid at 37°C is therefore 3.70, not 6.35, corresponding to a Ka of 2.0 × 10−4, which makes it a much stronger acid than Equation 16.63 suggests. Adding Equation 16.63 and Equation 16.64 and canceling H2CO3 from both sides give the following overall equation for the reaction of CO2 with water to give a proton and the bicarbonate ion:
Equation 16.65
The K value for the reaction in Equation 16.65 is the product of the true ionization constant for carbonic acid (Ka) and the equilibrium constant (K) for the reaction of CO2(aq) with water to give carbonic acid. The equilibrium equation for the reaction of CO2 with water to give bicarbonate and a proton is therefore
Equation 16.66
The presence of a gas in the equilibrium constant expression for a buffer is unusual. According to Henry’s law, where k is the Henry’s law constant for CO2, which is 3.0 × 10−5 M/mmHg at 37°C. (For more information about Henry’s law, see Chapter 13 "Solutions", Section 13.4 "Effects of Temperature and Pressure on Solubility".) Substituting this expression for [CO2] in Equation 16.66,
Equation 16.67
where is in mmHg. Taking the negative logarithm of both sides and rearranging,
Equation 16.68
Thus the pH of the solution depends on both the CO2 pressure over the solution and [HCO3−]. Figure 16.29 "Buffering in Blood: pH versus [HCO" plots the relationship between pH and [HCO3−] under physiological conditions for several different values of with normal pH and [HCO3−] values indicated by the dashed lines.
Figure 16.29 Buffering in Blood: pH versus [HCO3−] Curves for Buffers with Different Values of
Only those combinations of pH and [HCO3−] that lie on a given line are allowed for the particular value of indicated. Normal values of blood plasma pH and [HCO3−] are indicated by dashed lines.
According to Equation 16.65, adding a strong acid to the CO2/HCO3− system causes [HCO3−] to decrease as HCO3− is converted to CO2. Excess CO2 is released in the lungs and exhaled into the atmosphere, however, so there is essentially no change in Because the change in is small, Equation 16.68 predicts that the change in pH will also be rather small. Conversely, if a strong base is added, the OH− reacts with CO2 to form [HCO3−], but CO2 is replenished by the body, again limiting the change in both and pH. The CO2/HCO3− buffer system is an example of an open system, in which the total concentration of the components of the buffer change to keep the pH at a nearly constant value.
If a passenger steps out of an airplane in Denver, Colorado, for example, the lower at higher elevations (typically 31 mmHg at an elevation of 2000 m versus 40 mmHg at sea level) causes a shift to a new pH and [HCO3−]. The increase in pH and decrease in [HCO3−] in response to the decrease in are responsible for the general malaise that many people experience at high altitudes. If their blood pH does not adjust rapidly, the condition can develop into the life-threatening phenomenon known as altitude sickness.
Buffers are solutions that resist a change in pH after adding an acid or a base. Buffers contain a weak acid (HA) and its conjugate weak base (A−). Adding a strong electrolyte that contains one ion in common with a reaction system that is at equilibrium shifts the equilibrium in such a way as to reduce the concentration of the common ion. The shift in equilibrium is called the common ion effect. Buffers are characterized by their pH range and buffer capacity. The useful pH range of a buffer depends strongly on the chemical properties of the conjugate weak acid–base pair used to prepare the buffer (the Ka or Kb), whereas its buffer capacity depends solely on the concentrations of the species in the solution. The pH of a buffer can be calculated using the Henderson-Hasselbalch equation, which is valid for solutions whose concentrations are at least 100 times greater than their Ka values. Because no single buffer system can effectively maintain a constant pH value over the physiological range of approximately 5 to 7.4, biochemical systems use a set of buffers with overlapping ranges. The most important of these is the CO2/HCO3− system, which dominates the buffering action of blood plasma.
Explain why buffers are crucial for the proper functioning of biological systems.
What is the role of a buffer in chemistry and biology? Is it correct to say that buffers prevent a change in [H3O+]? Explain your reasoning.
Explain why the most effective buffers are those that contain approximately equal amounts of the weak acid and its conjugate base.
Which region of the titration curve of a weak acid or a weak base corresponds to the region of the smallest change in pH per amount of added strong acid or strong base?
If you were given a solution of sodium acetate, describe two ways you could convert the solution to a buffer.
Why are buffers usually used only within approximately one pH unit of the pKa or pKb of the parent weak acid or base?
The titration curve for a monoprotic acid can be divided into four regions: the starting point, the region around the midpoint of the titration, the equivalence point, and the region after the equivalence point. For which region would you use each approach to describe the behavior of the solution?
Which of the following will produce a buffer solution? Explain your reasoning in each case.
Which of the following will produce a buffer solution? Explain your reasoning in each case.
Use the definition of Kb for a weak base to derive the following expression, which is analogous to the Henderson-Hasselbalch equation but for a weak base (B) rather than a weak acid (HA):
Why do biological systems use overlapping buffer systems to maintain a constant pH?
The CO2/HCO3− buffer system of blood has an effective pKa of approximately 6.1, yet the normal pH of blood is 7.4. Why is CO2/HCO3− an effective buffer when the pKa is more than 1 unit below the pH of blood? What happens to the pH of blood when the CO2 pressure increases? when the O2 pressure increases?
Carbon dioxide produced during respiration is converted to carbonic acid (H2CO3). The pKa1 of carbonic acid is 6.35, and its pKa2 is 10.33. Write the equations corresponding to each pK value and predict the equilibrium position for each reaction.
Benzenesulfonic acid (pKa = 0.70) is synthesized by treating benzene with concentrated sulfuric acid. Calculate the following:
Phenol has a pKa of 9.99. Calculate the following:
Salicylic acid is used in the synthesis of acetylsalicylic acid, or aspirin. One gram dissolves in 460 mL of water to create a saturated solution with a pH of 2.40.
An intermediate used in the synthesis of perfumes is valeric acid, also called pentanoic acid. The pKa of pentanoic acid is 4.84 at 25°C.
Problems marked with a ♦ involve multiple concepts.
The analytical concentration of lactic acid in blood is generally less than 1.2 × 10−3 M, corresponding to the sum of [lactate] and [lactic acid]. During strenuous exercise, however, oxygen in the muscle tissue is depleted, and overproduction of lactic acid occurs. This leads to a condition known as lactic acidosis, which is characterized by elevated blood lactic acid levels (approximately 5.0 × 10−3 M). The pKa of lactic acid is 3.86.
When the internal temperature of a human reaches 105°F, immediate steps must be taken to prevent the person from having convulsions. At this temperature, Kw is approximately 2.94 × 10−14.
♦ The compound diphenhydramine (DPH) is the active ingredient in a number of over-the-counter antihistamine medications used to treat the runny nose and watery eyes associated with hay fever and other allergies. DPH is a derivative of trimethylamine (one methyl group is replaced by a more complex organic “arm” containing two phenyl rings):
The compound is sold as the water-soluble hydrochloride salt (DPH+Cl−). A tablet of diphenhydramine hydrochloride contains 25.0 mg of the active ingredient. Calculate the pH of the solution if two tablets are dissolved in 100 mL of water. The pKb of diphenhydramine is 5.47, and the formula mass of diphenhydramine hydrochloride is 291.81 amu.
♦ Epinephrine, a secondary amine, is used to counter allergic reactions as well as to bring patients out of anesthesia and cardiac arrest. The pKb of epinephrine is 4.31. What is the percent ionization in a 0.280 M solution? What is the percent ionization after enough solid epinephrine hydrochloride is added to make the final epinephrineH+ concentration 0.982 M? What is the final pH of the solution?
♦ Fluoroacetic acid is a poison that has been used by ranchers in the western United States. The ranchers place the poison in the carcasses of dead animals to kill coyotes that feed on them; unfortunately, however, eagles and hawks are also killed in the process. How many milliliters of 0.0953 M Ca(OH)2 are needed to completely neutralize 50.0 mL of 0.262 M fluoroacetic acid solution (pKa = 2.59)? What is the initial pH of the solution? What is the pH of the solution at the equivalence point?
Accidental ingestion of aspirin (acetylsalicylic acid) is probably the most common cause of childhood poisoning. Initially, salicylates stimulate the portion of the brain that controls breathing, resulting in hyperventilation (excessively intense breathing that lowers the in the lungs). Subsequently, a potentially serious rebound effect occurs, as the salicylates are converted to a weak acid, salicylic acid, in the body. Starting with the normal values of = 40 mmHg, pH = 7.40, and [HCO3−] = 24 nM, show what happens during the initial phase of respiratory stimulation and the subsequent phase of acid production. Why is the rebound effect dangerous?
Emphysema is a disease that reduces the efficiency of breathing. As a result, less CO2 is exchanged with the atmosphere. What effect will this have on blood pH, and [HCO3−]?
68.7 mL; 1.60; 7.85