We begin our discussion of thermodynamics by reviewing some important terms introduced in Chapter 5 "Energy Changes in Chemical Reactions". First, we need to distinguish between a system and its surroundings. A system is that part of the universe in which we are interested, such as a mixture of gases in a glass bulb or a solution of substances in a flask. The surroundings are everything else—the rest of the universe. We can therefore state the following:
Equation 18.1
system + surroundings = universeA closed system, such as the contents of a sealed jar, cannot exchange matter with its surroundings, whereas an open system can; in this case, we can convert a closed system (the jar) to an open system by removing the jar’s lid.
In Chapter 5 "Energy Changes in Chemical Reactions", we also introduced the concept of a state functionA property of a system whose magnitude depends on only the present state of the system, not its previous history., a property of a system that depends on only the present state of the system, not its history. Thus a change in a state function depends on only the difference between the initial and final states, not the pathway used to go from one to the other. To help understand the concept of a state function, imagine a person hiking up a mountain (Figure 18.1 "Altitude Is a State Function"). If the person is well trained and fit, he or she may be able to climb almost vertically to the top (path A), whereas another less athletic person may choose a path that winds gradually to the top (path B). If both hikers start from the same point at the base of the mountain and end up at the same point at the top, their net change in altitude will be the same regardless of the path chosen. Hence altitude is a state function. On the other hand, a person may or may not carry a heavy pack and may climb in hot weather or cold. These conditions would influence changes in the hiker’s fatigue level, which depends on the path taken and the conditions experienced. Fatigue, therefore, is not a state function. Thermodynamics is generally concerned with state functions and does not deal with how the change between the initial state and final state occurs.
Figure 18.1 Altitude Is a State Function
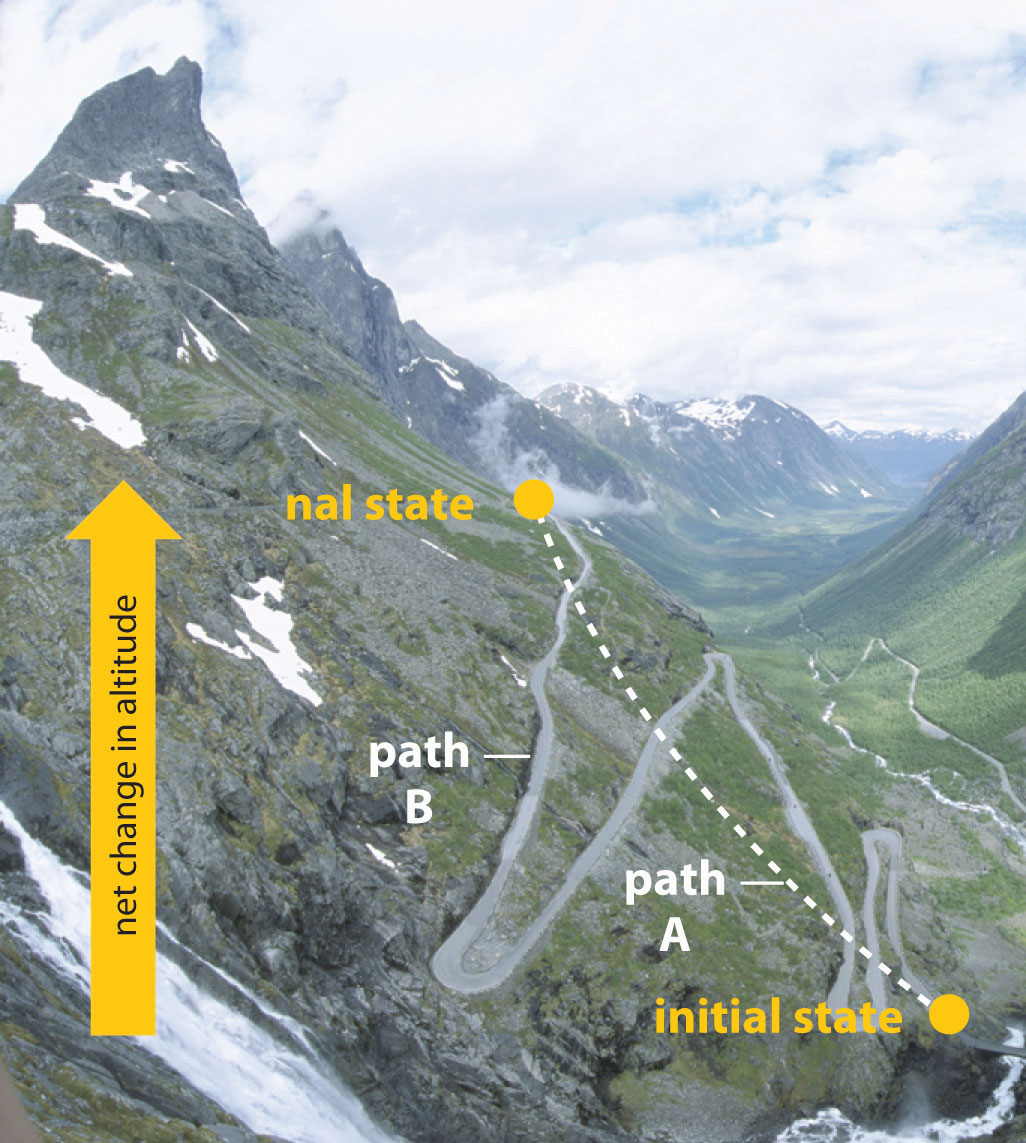
When hiking up a mountain, a person may decide to take path A, which is almost vertical, or path B, which gradually winds up to the top. Regardless of the path taken, the net change in altitude going from the initial state (bottom of the climb) to the final state (top of the climb) is the same. Thus altitude is a state function.
The internal energy (E)A state function that is the sum of the kinetic and potential energies of all a system’s components. of a system is the sum of the potential energy and the kinetic energy of all the components; internal energy is a state function. Although a closed system cannot exchange matter with its surroundings, it can exchange energy with its surroundings in two ways: by doing work or by releasing or absorbing heat—the flow of thermal energy. Work and heat are therefore two distinct ways of changing the internal energy of a system. We defined work (w) in Chapter 5 "Energy Changes in Chemical Reactions" as a force F acting through a distance d:
Equation 18.2
w = FdBecause work occurs only when an object, such as a person, or a substance, such as water, moves against an opposing force, work requires that a system and its surroundings be connected. In contrast, the flow of heat, the transfer of energy due to differences in temperature between two objects, represents a thermal connection between a system and its surroundings. Thus doing work causes a physical displacement, whereas the flow of heat causes a temperature change. The units of work and heat must be the same because both processes result in the transfer of energy. In the SI system, those units are joules (J), the same unit used for energy. There is no difference between an energy change brought about by doing work on a system and an equal energy change brought about by heating it.
The connections among work, heat, and energy were first described by Benjamin Thompson (1753–1814), an American-born scientist who was also known as Count Rumford. While supervising the manufacture of cannons, Rumford recognized the relationship between the amount of work required to drill out a cannon and the temperature of the water used to cool it during the drilling process (Figure 18.2 "The Relationship between Heat and Work"). At that time, it was generally thought that heat and work were separate and unrelated phenomena. Hence Rumford’s ideas were not widely accepted until many years later, after his findings had been corroborated in other laboratories.
Figure 18.2 The Relationship between Heat and Work

In the 1780s, an American scientist named Benjamin Thompson, also known as Count Rumford, was hired by the Elector of Bavaria to supervise the manufacture of cannons. During the manufacturing process, teams of horses harnessed to a large-toothed wheel supplied the power needed to drill a hole several inches in diameter straight down the center of a solid brass or bronze cylinder, which was cooled by water. Based on his observations, Rumford became convinced that heat and work are equivalent ways of transferring energy.
As we saw in Chapter 5 "Energy Changes in Chemical Reactions", there are many kinds of work, including mechanical work, electrical work, and work against a gravitational or a magnetic field. Here we will consider only mechanical work, focusing on the work done during changes in the pressure or the volume of a gas. To describe this pressure–volume work (PV work), we will use such imaginary oddities as frictionless pistons, which involve no component of resistance, and ideal gases, which have no attractive or repulsive interactions.
Imagine, for example, an ideal gas, confined by a frictionless piston, with internal pressure Pint and initial volume Vi (Figure 18.3). If Pext = Pint, the system is at equilibrium; the piston does not move, and no work is done. If the external pressure on the piston (Pext) is less than Pint, however, then the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings; that is, the final volume (Vf) will be greater than Vi. If Pext > Pint, then the gas will be compressed, and the surroundings will perform work on the system.
If the piston has cross-sectional area A, the external pressure exerted by the piston is, by definition, the force per unit area: Pext = F/A. The volume of any three-dimensional object with parallel sides (such as a cylinder) is the cross-sectional area times the height (V = Ah). Rearranging to give F = PextA and defining the distance the piston moves (d) as Δh, we can calculate the magnitude of the work performed by the piston by substituting into Equation 18.2:
Equation 18.3
w = Fd = PextAΔhFigure 18.3 PV Work
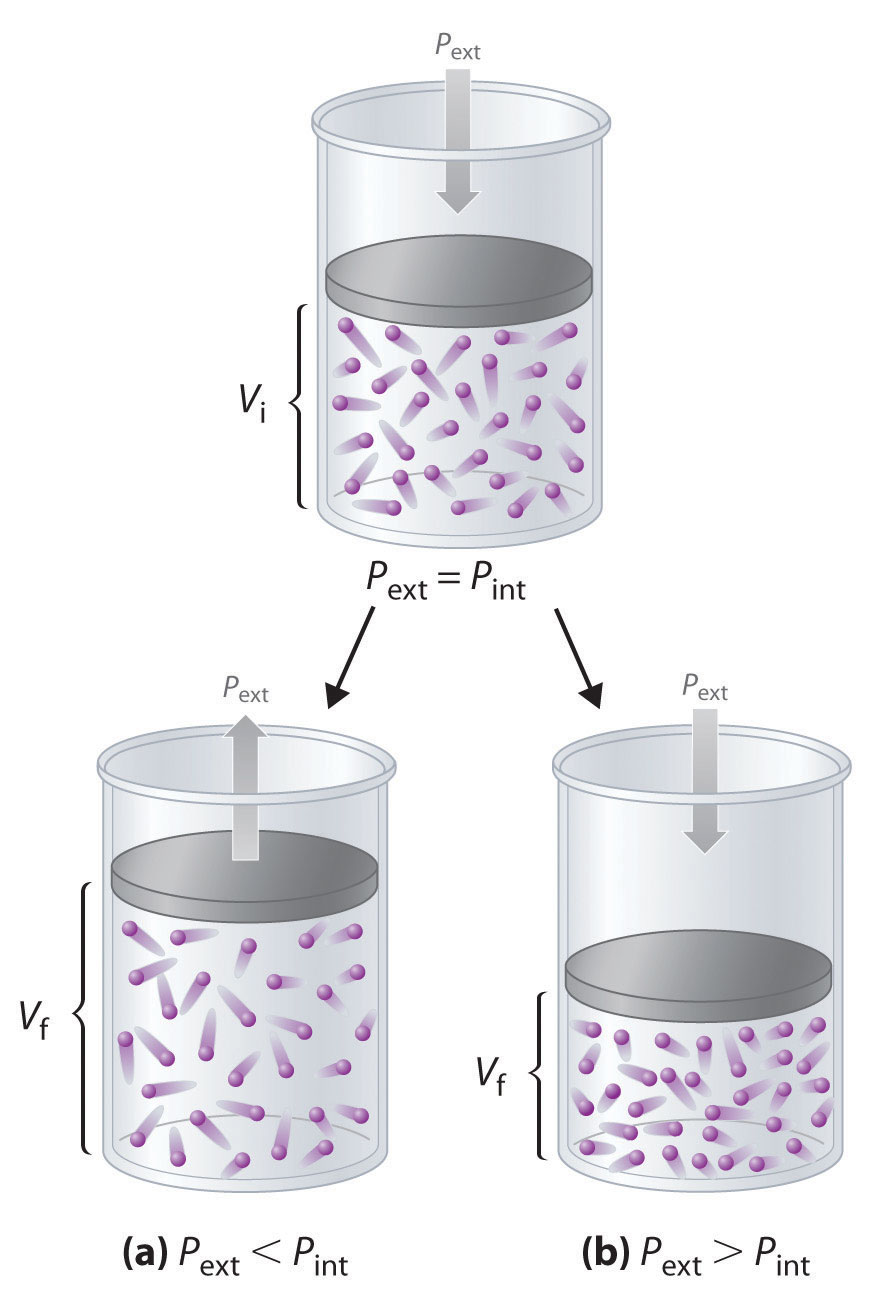
Using a frictionless piston, if the external pressure is less than Pint (a), the ideal gas inside the piston will expand, forcing the piston to perform work on its surroundings. The final volume (Vf) will be greater than Vi. Alternatively, if the external pressure is greater than Pint (b), the gas will be compressed, and the surroundings will perform work on the system.
The change in the volume of the cylinder (ΔV) as the piston moves a distance d is ΔV = AΔh, as shown in Figure 18.4 "Work Performed with a Change in Volume". The work performed is thus
Equation 18.4
w = PextΔVThe units of work obtained using this definition are correct for energy: pressure is force per unit area (newton/m2) and volume has units of cubic meters, so
Figure 18.4 Work Performed with a Change in Volume
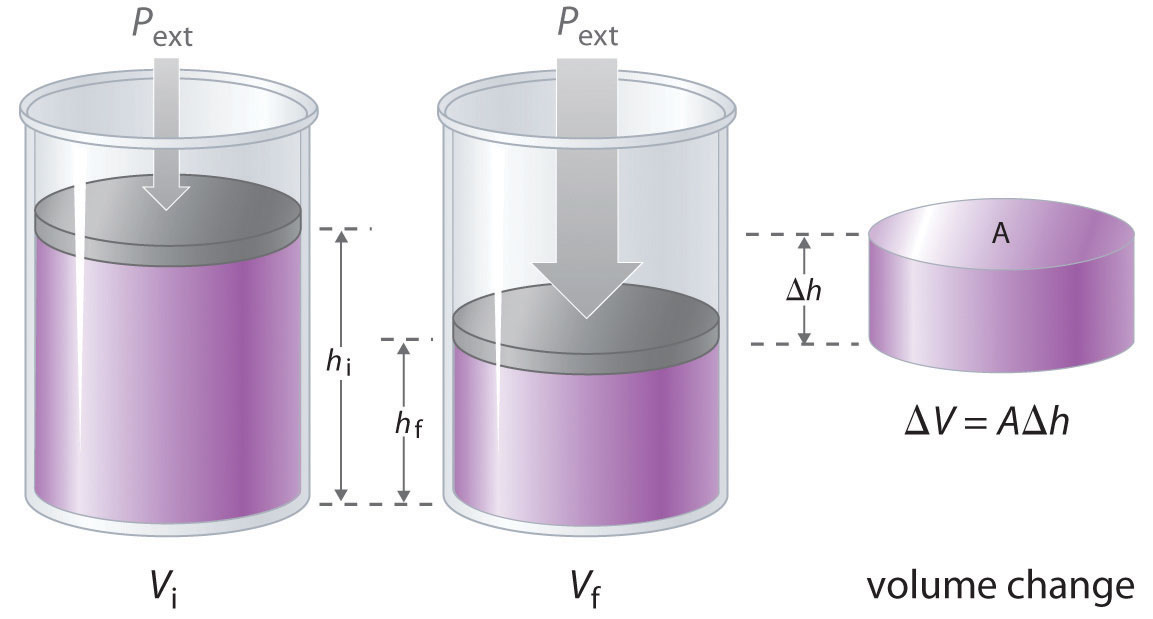
The change in the volume (ΔV) of the cylinder housing a piston is ΔV = AΔh as the piston moves. The work performed by the surroundings on the system as the piston moves inward is given by w = PextΔV.
If we use atmospheres for P and liters for V, we obtain units of L·atm for work. These units correspond to units of energy, as shown in the different values of the ideal gas constant R:
Thus 0.08206 L·atm = 8.314 J and 1 L·atm = 101.3 J. (For more information on the ideal gas law, see Chapter 10 "Gases".)
Whether work is defined as having a positive sign or a negative sign is a matter of convention. In Chapter 5 "Energy Changes in Chemical Reactions", we defined heat flow from a system to its surroundings as negative. Using that same sign convention, we define work done by a system on its surroundings as having a negative sign because it results in a transfer of energy from a system to its surroundings.This is an arbitrary convention and one that is not universally used. Some engineering disciplines are more interested in the work done on the surroundings than in the work done by the system and therefore use the opposite convention. Because ΔV > 0 for an expansion, Equation 18.4 must be written with a negative sign to describe PV work done by the system as negative:
Equation 18.5
w = −PextΔVThe work done by a gas expanding against an external pressure is therefore negative, corresponding to work done by a system on its surroundings. Conversely, when a gas is compressed by an external pressure, ΔV < 0 and the work is positive because work is being done on a system by its surroundings.
Suppose, for example, that the system under study is a mass of steam heated by the combustion of several hundred pounds of coal and enclosed within a cylinder housing a piston attached to the crankshaft of a large steam engine. The gas is not ideal, and the cylinder is not frictionless. Nonetheless, as steam enters the engine chamber and the expanding gas pushes against the piston, the piston moves, so useful work is performed. In fact, PV work launched the Industrial Revolution of the 19th century and powers the internal combustion engine on which most of us still rely for transportation.
In contrast to internal energy, work is not a state function. We can see this by examining Figure 18.5 "Work Is Not a State Function", in which two different, two-step pathways take a gaseous system from an initial state to a final state with corresponding changes in temperature. In pathway A, the volume of a gas is initially increased while its pressure stays constant (step 1); then its pressure is decreased while the volume remains constant (step 2). In pathway B, the order of the steps is reversed. The temperatures, pressures, and volumes of the initial and final states are identical in both cases, but the amount of work done, indicated by the shaded areas in the figure, is substantially different. As we can see, the amount of work done depends on the pathway taken from (V1, P1) to (V2, P2), which means that work is not a state function.
Internal energy is a state function, whereas work is not.
Figure 18.5 Work Is Not a State Function
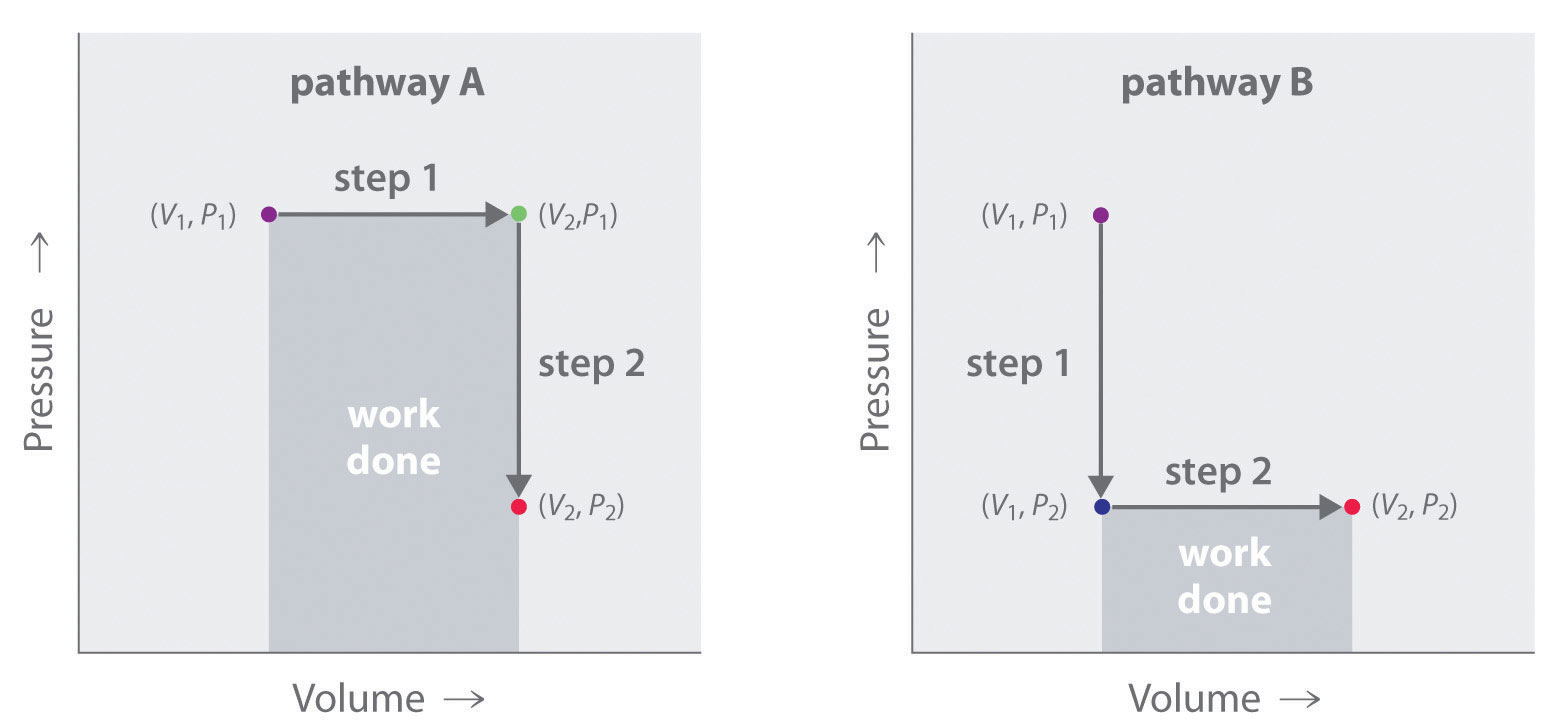
In pathway A, the volume of a gas is initially increased while its pressure stays constant (step 1). Its pressure is then decreased while the volume remains constant (step 2). Pathway B reverses these steps. Although (V1, P1) and (V2, P2) are identical in both cases, the amount of work done (shaded area) depends on the pathway taken.
A small high-performance internal combustion engine has six cylinders with a total nominal displacement (volume) of 2.40 L and a 10:1 compression ratio (meaning that the volume of each cylinder decreases by a factor of 10 when the piston compresses the air–gas mixture inside the cylinder prior to ignition). How much work in joules is done when a gas in one cylinder of the engine expands at constant temperature against an opposing pressure of 40.0 atm during the engine cycle? Assume that the gas is ideal, the piston is frictionless, and no energy is lost as heat.
Given: final volume, compression ratio, and external pressure
Asked for: work done
Strategy:
A Calculate the final volume of gas in a single cylinder. Then compute the initial volume of gas in a single cylinder from the compression ratio.
B Use Equation 18.5 to calculate the work done in liter-atmospheres. Convert from liter-atmospheres to joules.
Solution:
A To calculate the work done, we need to know the initial and final volumes. The final volume is the volume of one of the six cylinders with the piston all the way down: Vf = 2.40 L/6 = 0.400 L. With a 10:1 compression ratio, the volume of the same cylinder with the piston all the way up is Vi = 0.400 L/10 = 0.0400 L. Work is done by the system on its surroundings, so work is negative.
w = −PextΔV = −(40.0 atm)(0.400 L − 0.0400 L) = −14.4 L·atmConverting from liter-atmospheres to joules,
In the following exercise, you will see that the concept of work is not confined to engines and pistons. It is found in other applications as well.
Exercise
Breathing requires work, even if you are unaware of it. The lung volume of a 70 kg man at rest changed from 2200 mL to 2700 mL when he inhaled, while his lungs maintained a pressure of approximately 1.0 atm. How much work in liter-atmospheres and joules was required to take a single breath? During exercise, his lung volume changed from 2200 mL to 5200 mL on each in-breath. How much additional work in joules did he require to take a breath while exercising?
Answer: −0.500 L·atm, or −50.7 J; −304 J; if he takes a breath every three seconds, this corresponds to 1.4 Calories per minute (1.4 kcal).
Thermodynamics is the study of the interrelationships among heat, work, and the energy content of a system at equilibrium. The sum of the potential energy and the kinetic energy of all the components of a system is the internal energy (E) of the system, which is a state function. When the pressure or the volume of a gas is changed, any mechanical work done is called PV work. Work done by a system on its surroundings is given a negative value, whereas work done on a system by its surroundings has a positive value.
Thermodynamics focuses on the energetics of the reactants and products and provides information about the composition of the reaction system at equilibrium. What information on reaction systems is not provided by thermodynamics?
Given a system in which a substance can produce either of two possible products, A → B or A → C, which of the following can be predicted using chemical thermodynamics?
In what two ways can a closed system exchange energy with its surroundings? Are these two processes path dependent or path independent?
A microwave oven operates by providing enough energy to rotate water molecules, which produces heat. Can the change in the internal energy of a cup of water heated in a microwave oven be described as a state function? Can the heat produced be described as a state function?
Thermodynamics tells us nothing about the rate at which reactants are converted to products.
heat and work; path dependent
Calculate the work done in joules in each process.
How much work in joules is done when oxygen is compressed from a volume of 22.8 L and an external pressure of 1.20 atm to 12.0 L at a constant temperature? Was work done by the system or the surroundings?
Champagne is bottled at a CO2 pressure of about 5 atm. What is the force on the cork if its cross-sectional area is 2.0 cm2? How much work is done if a 2.0 g cork flies a distance of 8.2 ft straight into the air when the cork is popped? Was work done by the system or the surroundings?
One mole of water is converted to steam at 1.00 atm pressure and 100°C. Assuming ideal behavior, what is the change in volume when the water is converted from a liquid to a gas? If this transformation took place in a cylinder with a piston, how much work could be done by vaporizing the water at 1.00 atm? Is work done by the system or the surroundings?
Acceleration due to gravity on the earth’s surface is 9.8 m/s2. How much work is done by a 175 lb person going over Niagara Falls (approximately 520 ft high) in a barrel that weighs 145 lb?
Recall that force can be expressed as mass times acceleration (F = ma). Acceleration due to gravity on the earth’s surface is 9.8 m/s2.
A gas is allowed to expand from a volume of 2.3 L to a volume of 5.8 L. During the process, 460 J of heat is transferred from the surroundings to the gas.
One mole of an ideal gas is allowed to expand from an initial volume of 0.62 L to a final volume of 1.00 L at constant temperature against a constant external pressure of 1.0 atm. How much work has been done?
−230 kJ