In a galvanic cell, current is produced when electrons flow externally through the circuit from the anode to the cathode because of a difference in potential energy between the two electrodes in the electrochemical cell. In the Zn/Cu system, the valence electrons in zinc have a substantially higher potential energy than the valence electrons in copper because of shielding of the s electrons of zinc by the electrons in filled d orbitals. (For more information on atomic orbitals, see Chapter 6 "The Structure of Atoms", Section 6.5 "Atomic Orbitals and Their Energies".) Hence electrons flow spontaneously from zinc to copper(II) ions, forming zinc(II) ions and metallic copper (Figure 19.5 "Potential Energy Difference in the Zn/Cu System"). Just like water flowing spontaneously downhill, which can be made to do work by forcing a waterwheel, the flow of electrons from a higher potential energy to a lower one can also be harnessed to perform work.
Figure 19.5 Potential Energy Difference in the Zn/Cu System

The potential energy of a system consisting of metallic Zn and aqueous Cu2+ ions is greater than the potential energy of a system consisting of metallic Cu and aqueous Zn2+ ions. Much of this potential energy difference is because the valence electrons of metallic Zn are higher in energy than the valence electrons of metallic Cu. Because the Zn(s) + Cu2+(aq) system is higher in energy by 1.10 V than the Cu(s) + Zn2+(aq) system, energy is released when electrons are transferred from Zn to Cu2+ to form Cu and Zn2+.
Because the potential energy of valence electrons differs greatly from one substance to another, the voltage of a galvanic cell depends partly on the identity of the reacting substances. If we construct a galvanic cell similar to the one in part (a) in Figure 19.3 "The Reaction of Metallic Zinc with Aqueous Copper(II) Ions in a Galvanic Cell" but instead of copper use a strip of cobalt metal and 1 M Co2+ in the cathode compartment, the measured voltage is not 1.10 V but 0.51 V. Thus we can conclude that the difference in potential energy between the valence electrons of cobalt and zinc is less than the difference between the valence electrons of copper and zinc by 0.59 V.
The measured potential of a cell also depends strongly on the concentrations of the reacting species and the temperature of the system. To develop a scale of relative potentials that will allow us to predict the direction of an electrochemical reaction and the magnitude of the driving force for the reaction, the potentials for oxidations and reductions of different substances must be measured under comparable conditions. To do this, chemists use the standard cell potentialThe potential of an electrochemical cell measured under standard conditions (1 M for solutions, 1 atm for gases, and pure solids or pure liquids for other substances) and at a fixed temperature (usually 298 K). (E°cell), defined as the potential of a cell measured under standard conditions—that is, with all species in their standard states (1 M for solutions,Concentrated solutions of salts (about 1 M) generally do not exhibit ideal behavior, and the actual standard state corresponds to an activity of 1 rather than a concentration of 1 M. Corrections for nonideal behavior are important for precise quantitative work but not for the more qualitative approach that we are taking here. 1 atm for gases, pure solids or pure liquids for other substances) and at a fixed temperature, usually 25°C.
Measured redox potentials depend on the potential energy of valence electrons, the concentrations of the species in the reaction, and the temperature of the system.
It is physically impossible to measure the potential of a single electrode: only the difference between the potentials of two electrodes can be measured. (This is analogous to measuring absolute enthalpies or free energies. Recall from Chapter 18 "Chemical Thermodynamics" that only differences in enthalpy and free energy can be measured.) We can, however, compare the standard cell potentials for two different galvanic cells that have one kind of electrode in common. This allows us to measure the potential difference between two dissimilar electrodes. For example, the measured standard cell potential (E°) for the Zn/Cu system is 1.10 V, whereas E° for the corresponding Zn/Co system is 0.51 V. This implies that the potential difference between the Co and Cu electrodes is 1.10 V − 0.51 V = 0.59 V. In fact, that is exactly the potential measured under standard conditions if a cell is constructed with the following cell diagram:
Equation 19.9
This cell diagram corresponds to the oxidation of a cobalt anode and the reduction of Cu2+ in solution at the copper cathode.
All tabulated values of standard electrode potentials by convention are listed for a reaction written as a reduction, not as an oxidation, to be able to compare standard potentials for different substances. (Standard electrode potentials for various reduction reactions are given in Chapter 29 "Appendix E: Standard Reduction Potentials at 25°C".) The standard cell potential (E°cell) is therefore the difference between the tabulated reduction potentials of the two half-reactions, not their sum:
Equation 19.10
E°cell = E°cathode − E°anodeIn contrast, recall that half-reactions are written to show the reduction and oxidation reactions that actually occur in the cell, so the overall cell reaction is written as the sum of the two half-reactions. According to Equation 19.10, when we know the standard potential for any single half-reaction, we can obtain the value of the standard potential of many other half-reactions by measuring the standard potential of the corresponding cell.
The overall cell reaction is the sum of the two half-reactions, but the cell potential is the difference between the reduction potentials: E°cell = E°cathode − E°anode.
Although it is impossible to measure the potential of any electrode directly, we can choose a reference electrode whose potential is defined as 0 V under standard conditions. The standard hydrogen electrode (SHE)The electrode chosen as the reference for all other electrodes, which has been assigned a standard potential of 0 V and consists of a Pt wire in contact with an aqueous solution that contains 1 M in equilibrium with gas at a pressure of 1 atm at the Pt-solution interface. is universally used for this purpose and is assigned a standard potential of 0 V. It consists of a strip of platinum wire in contact with an aqueous solution containing 1 M H+. The [H+] in solution is in equilibrium with H2 gas at a pressure of 1 atm at the Pt-solution interface (Figure 19.6 "The Standard Hydrogen Electrode"). Protons are reduced or hydrogen molecules are oxidized at the Pt surface according to the following equation:
Equation 19.11
One especially attractive feature of the SHE is that the Pt metal electrode is not consumed during the reaction.
Figure 19.6 The Standard Hydrogen Electrode
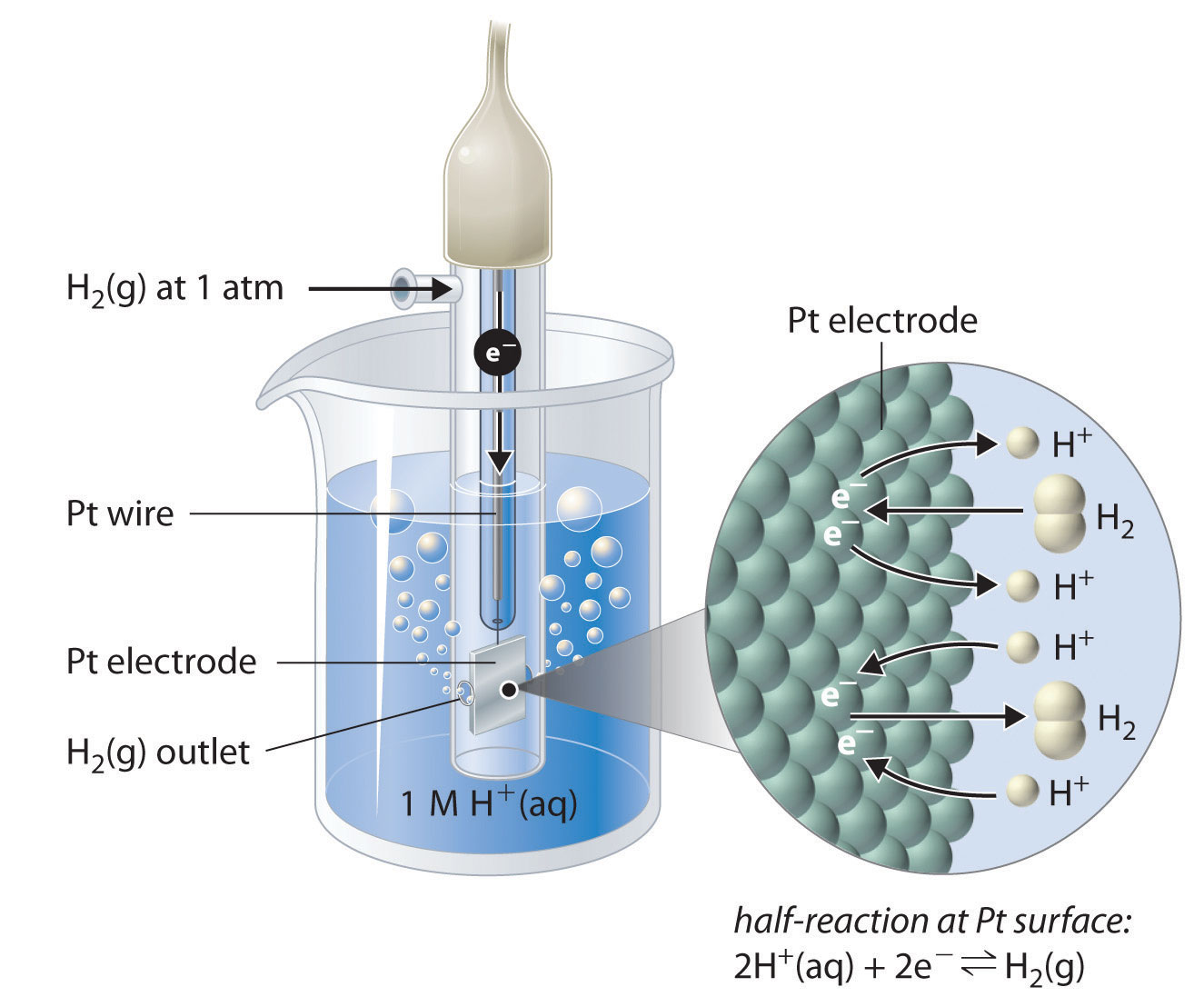
The SHE consists of platinum wire that is connected to a Pt surface in contact with an aqueous solution containing 1 M H+ in equilibrium with H2 gas at a pressure of 1 atm. In the molecular view, the Pt surface catalyzes the oxidation of hydrogen molecules to protons or the reduction of protons to hydrogen gas. (Water is omitted for clarity.) The standard potential of the SHE is arbitrarily assigned a value of 0 V.
Figure 19.7 "Determining a Standard Electrode Potential Using a Standard Hydrogen Electrode" shows a galvanic cell that consists of a SHE in one beaker and a Zn strip in another beaker containing a solution of Zn2+ ions. When the circuit is closed, the voltmeter indicates a potential of 0.76 V. The zinc electrode begins to dissolve to form Zn2+, and H+ ions are reduced to H2 in the other compartment. Thus the hydrogen electrode is the cathode, and the zinc electrode is the anode. The diagram for this galvanic cell is as follows:
Equation 19.12
Zn(s)∣Zn2+(aq)∥H+(aq, 1 M)∣H2(g, 1 atm)∣Pt(s)The half-reactions that actually occur in the cell and their corresponding electrode potentials are as follows:
Equation 19.13
Equation 19.14
Equation 19.15
Figure 19.7 Determining a Standard Electrode Potential Using a Standard Hydrogen Electrode
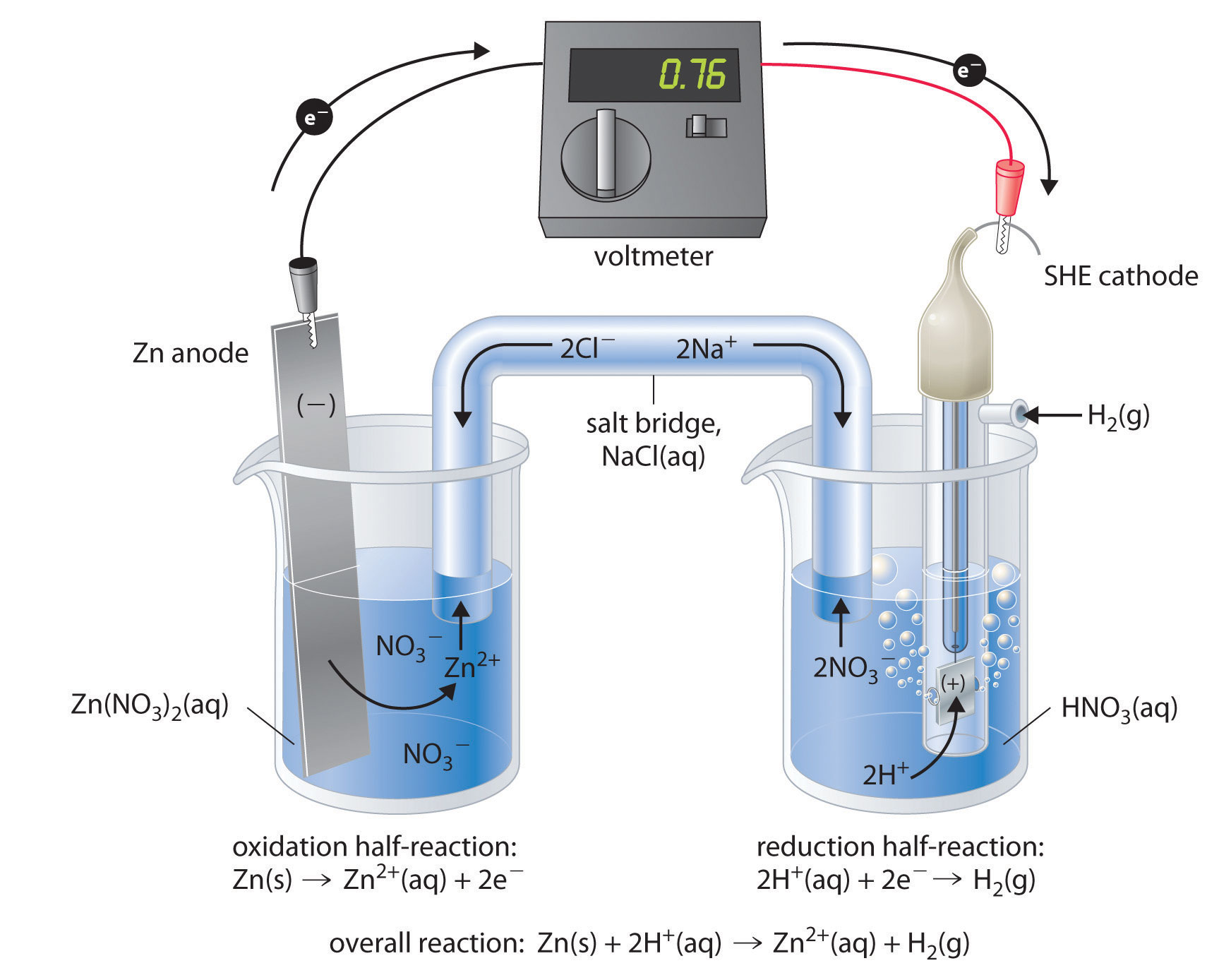
The voltmeter shows that the standard cell potential of a galvanic cell consisting of a SHE and a Zn/Zn2+ couple is E°cell = 0.76 V. Because the zinc electrode in this cell dissolves spontaneously to form Zn2+(aq) ions while H+(aq) ions are reduced to H2 at the platinum surface, the standard electrode potential of the Zn2+/Zn couple is −0.76 V.
Although the reaction at the anode is an oxidation, by convention its tabulated E° value is reported as a reduction potential. The potential of a half-reaction measured against the SHE under standard conditions is called the standard electrode potentialThe potential of a half-reaction measured against the SHE under standard conditions. for that half-reaction.In this example, the standard reduction potential for Zn2+(aq) + 2e− → Zn(s) is −0.76 V, which means that the standard electrode potential for the reaction that occurs at the anode, the oxidation of Zn to Zn2+, often called the Zn/Zn2+ redox couple, or the Zn/Zn2+ couple, is −(−0.76 V) = 0.76 V. We must therefore subtract E°anode from E°cathode to obtain E°cell: 0 − (−0.76 V) = 0.76 V.
Because electrical potential is the energy needed to move a charged particle in an electric field, standard electrode potentials for half-reactions are intensive properties and do not depend on the amount of substance involved. Consequently, E° values are independent of the stoichiometric coefficients for the half-reaction, and, most important, the coefficients used to produce a balanced overall reaction do not affect the value of the cell potential.
E° values do not depend on the stoichiometric coefficients for a half-reaction.
To measure the potential of the Cu/Cu2+ couple, we can construct a galvanic cell analogous to the one shown in Figure 19.7 "Determining a Standard Electrode Potential Using a Standard Hydrogen Electrode" but containing a Cu/Cu2+ couple in the sample compartment instead of Zn/Zn2+. When we close the circuit this time, the measured potential for the cell is negative (−0.34 V) rather than positive. The negative value of E°cell indicates that the direction of spontaneous electron flow is the opposite of that for the Zn/Zn2+ couple. Hence the reactions that occur spontaneously, indicated by a positive E°cell, are the reduction of Cu2+ to Cu at the copper electrode. The copper electrode gains mass as the reaction proceeds, and H2 is oxidized to H+ at the platinum electrode. In this cell, the copper strip is the cathode, and the hydrogen electrode is the anode. The cell diagram therefore is written with the SHE on the left and the Cu2+/Cu couple on the right:
Equation 19.16
Pt(s)∣H2(g, 1 atm)∣H+(aq, 1 M)∥Cu2+(aq, 1 M)∣Cu(s)The half-cell reactions and potentials of the spontaneous reaction are as follows:
Equation 19.17
Equation 19.18
Equation 19.19
Thus the standard electrode potential for the Cu2+/Cu couple is 0.34 V.
In Chapter 4 "Reactions in Aqueous Solution", we described a method for balancing redox reactions using oxidation numbers. Oxidation numbers were assigned to each atom in a redox reaction to identify any changes in the oxidation states. Here we present an alternative approach to balancing redox reactions, the half-reaction method, in which the overall redox reaction is divided into an oxidation half-reaction and a reduction half-reaction, each balanced for mass and charge. This method more closely reflects the events that take place in an electrochemical cell, where the two half-reactions may be physically separated from each other.
We can illustrate how to balance a redox reaction using half-reactions with the reaction that occurs when Drano, a commercial solid drain cleaner, is poured into a clogged drain. Drano contains a mixture of sodium hydroxide and powdered aluminum, which in solution reacts to produce hydrogen gas:
Equation 19.20
Al(s) + OH−(aq) → Al(OH)4−(aq) + H2(g)In this reaction, Al(s) is oxidized to Al3+, and H+ in water is reduced to H2 gas, which bubbles through the solution, agitating it and breaking up the clogs.
The overall redox reaction is composed of a reduction half-reaction and an oxidation half-reaction. From the standard electrode potentials listed in Chapter 29 "Appendix E: Standard Reduction Potentials at 25°C", we find the corresponding half-reactions that describe the reduction of H+ ions in water to H2 and the oxidation of Al to Al3+ in basic solution:
Equation 19.21
reduction: 2H2O(l) + 2e− → 2OH−(aq) + H2(g)Equation 19.22
oxidation: Al(s) + 4OH−(aq) → Al(OH)4−(aq) + 3e−The half-reactions chosen must exactly reflect the reaction conditions, such as the basic conditions shown here. Moreover, the physical states of the reactants and the products must be identical to those given in the overall reaction, whether gaseous, liquid, solid, or in solution.
In Equation 19.21, two H+ ions gain one electron each in the reduction; in Equation 19.22, the aluminum atom loses three electrons in the oxidation. The charges are balanced by multiplying the reduction half-reaction (Equation 19.21) by 3 and the oxidation half-reaction (Equation 19.22) by 2 to give the same number of electrons in both half-reactions:
Equation 19.23
reduction: 6H2O(l) + 6e− → 6OH−(aq) + 3H2(g)Equation 19.24
oxidation: 2Al(s) + 8OH−(aq) → 2Al(OH)4−(aq) + 6e−Adding the two half-reactions,
Equation 19.25
6H2O(l) + 2Al(s) + 8OH−(aq) → 2Al(OH)4−(aq) + 3H2(g) + 6OH−(aq)Simplifying by canceling substances that appear on both sides of the equation,
Equation 19.26
6H2O(l) + 2Al(s) + 2OH−(aq) → 2Al(OH)4−(aq) + 3H2(g)We have a −2 charge on the left side of the equation and a −2 charge on the right side. Thus the charges are balanced, but we must also check that atoms are balanced:
Equation 19.27
2Al + 8O + 14H = 2Al + 8O + 14HThe atoms also balance, so Equation 19.26 is a balanced chemical equation for the redox reaction depicted in Equation 19.20.
The half-reaction method requires that half-reactions exactly reflect reaction conditions, and the physical states of the reactants and the products must be identical to those in the overall reaction.
We can also balance a redox reaction by first balancing the atoms in each half-reaction and then balancing the charges. With this alternative method, we do not need to use the half-reactions listed in Chapter 29 "Appendix E: Standard Reduction Potentials at 25°C" but instead focus on the atoms whose oxidation states change, as illustrated in the following steps:
Step 1: Write the reduction half-reaction and the oxidation half-reaction.
For the reaction shown in Equation 19.20, hydrogen is reduced from H+ in OH− to H2, and aluminum is oxidized from Al0 to Al3+:
Equation 19.28
reduction: OH−(aq) → H2(g)Equation 19.29
oxidation: Al(s) → Al(OH)4−(aq)Step 2: Balance the atoms by balancing elements other than O and H. Then balance O atoms by adding H2O and balance H atoms by adding H+.
Elements other than O and H in the previous two equations are balanced as written, so we proceed with balancing the O atoms. We can do this by adding water to the appropriate side of each half-reaction:
Equation 19.30
reduction: OH−(aq) → H2(g) + H2O(l)Equation 19.31
oxidation: Al(s) + 4H2O(l) → Al(OH)4−(aq)Balancing H atoms by adding H+, we obtain the following:
Equation 19.32
reduction: OH−(aq) + 3H+(aq) → H2(g) + H2O(l)Equation 19.33
oxidation: Al(s) + 4H2O(l) → Al(OH)4−(aq) + 4H+(aq)We have now balanced the atoms in each half-reaction, but the charges are not balanced.
Step 3: Balance the charges in each half-reaction by adding electrons.
Two electrons are gained in the reduction of H+ ions to H2, and three electrons are lost during the oxidation of Al0 to Al3+:
Equation 19.34
reduction: OH−(aq) + 3H+(aq) + 2e− → H2(g) + H2O(l)Equation 19.35
oxidation: Al(s) + 4H2O(l) → Al(OH)4−(aq) + 4H+(aq) + 3e−Step 4: Multiply the reductive and oxidative half-reactions by appropriate integers to obtain the same number of electrons in both half-reactions.
In this case, we multiply Equation 19.34 (the reductive half-reaction) by 3 and Equation 19.35 (the oxidative half-reaction) by 2 to obtain the same number of electrons in both half-reactions:
Equation 19.36
reduction: 3OH−(aq) + 9H+(aq) + 6e− → 3H2(g) + 3H2O(l)Equation 19.37
oxidation: 2Al(s) + 8H2O(l) → 2Al(OH)4−(aq) + 8H+(aq) + 6e−Step 5: Add the two half-reactions and cancel substances that appear on both sides of the equation.
Adding and, in this case, canceling 8H+, 3H2O, and 6e−,
Equation 19.38
2Al(s) + 5H2O(l) + 3OH−(aq) + H+(aq) → 2Al(OH)4−(aq) + 3H2(g)We have three OH− and one H+ on the left side. Neutralizing the H+ gives us a total of 5H2O + H2O = 6H2O and leaves 2OH− on the left side:
Equation 19.39
2Al(s) + 6H2O(l) + 2OH−(aq) → 2Al(OH)4−(aq) + 3H2(g)Step 6: Check to make sure that all atoms and charges are balanced.
Equation 19.39 is identical to Equation 19.26, obtained using the first method, so the charges and numbers of atoms on each side of the equation balance.
Figure 19.8 The Reaction of Dichromate with Iodide

The reaction of a yellow solution of sodium dichromate with a colorless solution of sodium iodide produces a deep amber solution that contains a green Cr3+(aq) complex and brown I2(aq) ions.
In acidic solution, the redox reaction of dichromate ion (Cr2O72−) and iodide (I−) can be monitored visually. The yellow dichromate solution reacts with the colorless iodide solution to produce a solution that is deep amber due to the presence of a green Cr3+(aq) complex and brown I2(aq) ions (Figure 19.8 "The Reaction of Dichromate with Iodide"):
Cr2O72−(aq) + I−(aq) → Cr3+(aq) + I2(aq)Balance this equation using half-reactions.
Given: redox reaction and Chapter 29 "Appendix E: Standard Reduction Potentials at 25°C"
Asked for: balanced chemical equation using half-reactions
Strategy:
Follow the steps to balance the redox reaction using the half-reaction method.
Solution:
From the standard electrode potentials listed in Chapter 29 "Appendix E: Standard Reduction Potentials at 25°C", we find the half-reactions corresponding to the overall reaction:
reduction: Cr2O72−(aq) + 14H+(aq) + 6e− → 2Cr3+(aq) + 7H2O(l) oxidation: 2I−(aq) → I2(aq) + 2e−Balancing the number of electrons by multiplying the oxidation reaction by 3,
oxidation: 6I−(aq) → 3I2(aq) + 6e−Adding the two half-reactions and canceling electrons,
Cr2O72−(aq) + 14H+(aq) + 6I−(aq) → 2Cr3+(aq) + 7H2O(l) + 3I2(aq)We must now check to make sure the charges and atoms on each side of the equation balance:
The charges and atoms balance, so our equation is balanced.
We can also use the alternative procedure, which does not require the half-reactions listed in Chapter 29 "Appendix E: Standard Reduction Potentials at 25°C".
Step 1: Chromium is reduced from Cr6+ in Cr2O72−to Cr3+, and I− ions are oxidized to I2. Dividing the reaction into two half-reactions,
reduction: Cr2O72−(aq) → Cr3+(aq) oxidation: I−(aq) → I2(aq)Step 2: Balancing the atoms other than oxygen and hydrogen,
reduction: Cr2O72−(aq) → 2Cr3+(aq) oxidation: 2I−(aq) → I2(aq)We now balance the O atoms by adding H2O—in this case, to the right side of the reduction half-reaction. Because the oxidation half-reaction does not contain oxygen, it can be ignored in this step.
reduction: Cr2O72−(aq) → 2Cr3+(aq) + 7H2O(l)Next we balance the H atoms by adding H+ to the left side of the reduction half-reaction. Again, we can ignore the oxidation half-reaction.
reduction: Cr2O72−(aq) + 14H+(aq) → + 2Cr3+(aq) + 7H2O(l)Step 3: We must now add electrons to balance the charges. The reduction half-reaction (2Cr+6 to 2Cr+3) has a +12 charge on the left and a +6 charge on the right, so six electrons are needed to balance the charge. The oxidation half-reaction (2I− to I2) has a −2 charge on the left side and a 0 charge on the right, so it needs two electrons to balance the charge:
reduction: Cr2O72−(aq) + 14H+(aq) + 6e− → 2Cr3+(aq) + 7H2O(l) oxidation: 2I−(aq) → I2(aq) + 2e−Step 4: To have the same number of electrons in both half-reactions, we must multiply the oxidation half-reaction by 3:
oxidation: 6I−(aq) → 3I2(s) + 6e−Step 5: Adding the two half-reactions and canceling substances that appear in both reactions,
Cr2O72−(aq) + 14H+(aq) + 6I−(aq) → 2Cr3+(aq) + 7H2O(l) + 3I2(aq)Step 6: This is the same equation we obtained using the first method. Thus the charges and atoms on each side of the equation balance.
Exercise
Copper is commonly found as the mineral covellite (CuS). The first step in extracting the copper is to dissolve the mineral in nitric acid (HNO3), which oxidizes sulfide to sulfate and reduces nitric acid to NO:
CuS(s) + HNO3(aq) → NO(g) + CuSO4(aq)Balance this equation using the half-reaction method.
Answer: 3CuS(s) + 8HNO3(aq) → 8NO(g) + 3CuSO4(aq) + 4H2O(l)
The standard cell potential for a redox reaction (E°cell) is a measure of the tendency of reactants in their standard states to form products in their standard states; consequently, it is a measure of the driving force for the reaction, which earlier we called voltage. We can use the two standard electrode potentials we found earlier to calculate the standard potential for the Zn/Cu cell represented by the following cell diagram:
Equation 19.40
Zn(s)∣Zn2+(aq, 1 M)∥Cu2+(aq, 1 M)∣Cu(s)We know the values of E°anode for the reduction of Zn2+ and E°cathode for the reduction of Cu2+, so we can calculate E°cell:
Equation 19.41
Equation 19.42
Equation 19.43
This is the same value that is observed experimentally. If the value of E°cell is positive, the reaction will occur spontaneously as written. If the value of E°cell is negative, then the reaction is not spontaneous, and it will not occur as written under standard conditions; it will, however, proceed spontaneously in the opposite direction.As we shall see in Section 19.7 "Electrolysis", this does not mean that the reaction cannot be made to occur at all under standard conditions. With a sufficient input of electrical energy, virtually any reaction can be forced to occur. Example 4 and its corresponding exercise illustrate how we can use measured cell potentials to calculate standard potentials for redox couples.
A positive E°cell means that the reaction will occur spontaneously as written. A negative E°cell means that the reaction will proceed spontaneously in the opposite direction.
A galvanic cell with a measured standard cell potential of 0.27 V is constructed using two beakers connected by a salt bridge. One beaker contains a strip of gallium metal immersed in a 1 M solution of GaCl3, and the other contains a piece of nickel immersed in a 1 M solution of NiCl2. The half-reactions that occur when the compartments are connected are as follows:
cathode: Ni2+(aq) + 2e− → Ni(s) anode: Ga(s) → Ga3+(aq) + 3e−If the potential for the oxidation of Ga to Ga3+ is 0.55 V under standard conditions, what is the potential for the oxidation of Ni to Ni2+?
Given: galvanic cell, half-reactions, standard cell potential, and potential for the oxidation half-reaction under standard conditions
Asked for: standard electrode potential of reaction occurring at the cathode
Strategy:
A Write the equation for the half-reaction that occurs at the anode along with the value of the standard electrode potential for the half-reaction.
B Use Equation 19.10 to calculate the standard electrode potential for the half-reaction that occurs at the cathode. Then reverse the sign to obtain the potential for the corresponding oxidation half-reaction under standard conditions.
Solution:
A We have been given the potential for the oxidation of Ga to Ga3+ under standard conditions, but to report the standard electrode potential, we must reverse the sign. For the reduction reaction Ga3+(aq) + 3e− → Ga(s), E°anode = −0.55 V.
B Using the value given for E°cell and the calculated value of E°anode, we can calculate the standard potential for the reduction of Ni2+ to Ni from Equation 19.10:
This is the standard electrode potential for the reaction Ni2+(aq) + 2e− → Ni(s). Because we are asked for the potential for the oxidation of Ni to Ni2+ under standard conditions, we must reverse the sign of E°cathode. Thus E° = −(−0.28 V) = 0.28 V for the oxidation. With three electrons consumed in the reduction and two produced in the oxidation, the overall reaction is not balanced. Recall, however, that standard potentials are independent of stoichiometry.
Exercise
A galvanic cell is constructed with one compartment that contains a mercury electrode immersed in a 1 M aqueous solution of mercuric acetate [Hg(CH3CO2)2] and one compartment that contains a strip of magnesium immersed in a 1 M aqueous solution of MgCl2. When the compartments are connected, a potential of 3.22 V is measured and the following half-reactions occur:
cathode: Hg2+(aq) + 2e− → Hg(l) anode: Mg(s) → Mg2+(aq) + 2e−If the potential for the oxidation of Mg to Mg2+ is 2.37 V under standard conditions, what is the standard electrode potential for the reaction that occurs at the anode?
Answer: 0.85 V
When using a galvanic cell to measure the concentration of a substance, we are generally interested in the potential of only one of the electrodes of the cell, the so-called indicator electrodeThe electrode of a galvanic cell whose potential is related to the concentration of the substance being measured., whose potential is related to the concentration of the substance being measured. To ensure that any change in the measured potential of the cell is due to only the substance being analyzed, the potential of the other electrode, the reference electrodeAn electrode in an galvanic cell whose potential is unaffected by the properties of the solution., must be constant. You are already familiar with one example of a reference electrode: the SHE. The potential of a reference electrode must be unaffected by the properties of the solution, and if possible, it should be physically isolated from the solution of interest. To measure the potential of a solution, we select a reference electrode and an appropriate indicator electrode. Whether reduction or oxidation of the substance being analyzed occurs depends on the potential of the half-reaction for the substance of interest (the sample) and the potential of the reference electrode.
The potential of any reference electrode should not be affected by the properties of the solution to be analyzed, and it should also be physically isolated.
There are many possible choices of reference electrode other than the SHE. The SHE requires a constant flow of highly flammable hydrogen gas, which makes it inconvenient to use. Consequently, two other electrodes are commonly chosen as reference electrodes. One is the silver–silver chloride electrodeA reference electrode that consists of a silver wire coated with a very thin layer of AgCl and dipped into a chloride ion solution with a fixed concentration., which consists of a silver wire coated with a very thin layer of AgCl that is dipped into a chloride ion solution with a fixed concentration. The cell diagram and reduction half-reaction are as follows:
Equation 19.44
If a saturated solution of KCl is used as the chloride solution, the potential of the silver–silver chloride electrode is 0.197 V versus the SHE. That is, 0.197 V must be subtracted from the measured value to obtain the standard electrode potential measured against the SHE.
A second common reference electrode is the saturated calomel electrode (SCE)A reference electrode that consists of a platinum wire inserted into a moist paste of liquid mercury (calomel; ) and KCl in an interior cell, which is surrounded by an aqueous KCl solution., which has the same general form as the silver–silver chloride electrode. The SCE consists of a platinum wire inserted into a moist paste of liquid mercury (Hg2Cl2; called calomel in the old chemical literature) and KCl. This interior cell is surrounded by an aqueous KCl solution, which acts as a salt bridge between the interior cell and the exterior solution (part (a) in Figure 19.9 "Three Common Types of Electrodes"). Although it sounds and looks complex, this cell is actually easy to prepare and maintain, and its potential is highly reproducible. The SCE cell diagram and corresponding half-reaction are as follows:
Equation 19.45
Pt(s)∣Hg2Cl2(s)∣KCl(aq, sat)Equation 19.46
Hg2Cl2(s) + 2e− → 2Hg(l) + 2Cl−(aq)Figure 19.9 Three Common Types of Electrodes
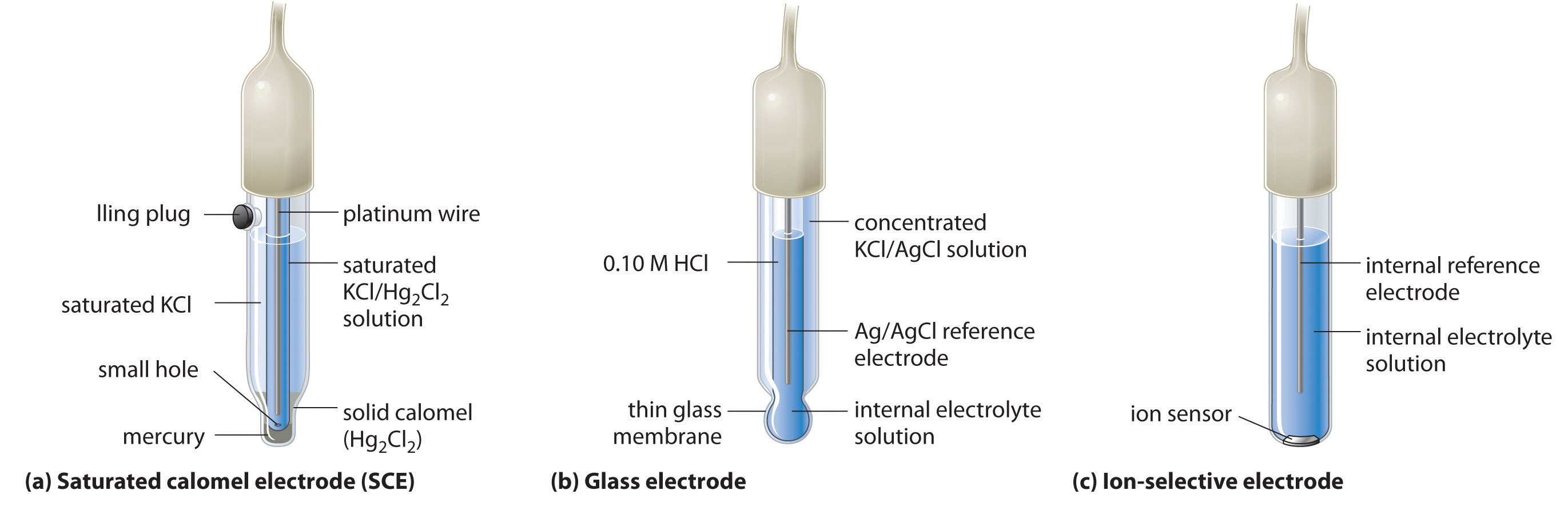
(a) The SCE is a reference electrode that consists of a platinum wire inserted into a moist paste of liquid mercury (calomel; Hg2Cl2) and KCl. The interior cell is surrounded by an aqueous KCl solution, which acts as a salt bridge between the interior cell and the exterior solution. (b) In a glass electrode, an internal Ag/AgCl electrode is immersed in a 1 M HCl solution that is separated from the sample solution by a very thin glass membrane. The potential of the electrode depends on the H+ ion concentration of the sample. (c) The potential of an ion-selective electrode depends on the concentration of only a single ionic species in solution.
At 25°C, the potential of the SCE is 0.2415 V versus the SHE, which means that 0.2415 V must be subtracted from the potential versus an SCE to obtain the standard electrode potential.
One of the most common uses of electrochemistry is to measure the H+ ion concentration of a solution. A glass electrodeAn electrode used to measure the ion concentration of a solution and consisting of an internal Ag/AgCl electrode immersed in a 1 M HCl solution that is separated from the solution by a very thin glass membrane. is generally used for this purpose, in which an internal Ag/AgCl electrode is immersed in a 0.10 M HCl solution that is separated from the solution by a very thin glass membrane (part (b) in Figure 19.9 "Three Common Types of Electrodes"). The glass membrane absorbs protons, which affects the measured potential. The extent of the adsorption on the inner side is fixed because [H+] is fixed inside the electrode, but the adsorption of protons on the outer surface depends on the pH of the solution. The potential of the glass electrode depends on [H+] as follows (recall that pH = −log[H+]:
Equation 19.47
Eglass = E′ + (0.0591 V × log[H+]) = E′ − 0.0591 V × pHThe voltage E′ is a constant that depends on the exact construction of the electrode. Although it can be measured, in practice, a glass electrode is calibrated; that is, it is inserted into a solution of known pH, and the display on the pH meter is adjusted to the known value. Once the electrode is properly calibrated, it can be placed in a solution and used to determine an unknown pH.
Ion-selective electrodesAn electrode whose potential depends on only the concentration of a particular species in solution. are used to measure the concentration of a particular species in solution; they are designed so that their potential depends on only the concentration of the desired species (part (c) in Figure 19.9 "Three Common Types of Electrodes"). These electrodes usually contain an internal reference electrode that is connected by a solution of an electrolyte to a crystalline inorganic material or a membrane, which acts as the sensor. For example, one type of ion-selective electrode uses a single crystal of Eu-doped LaF3 as the inorganic material. When fluoride ions in solution diffuse to the surface of the solid, the potential of the electrode changes, resulting in a so-called fluoride electrode. Similar electrodes are used to measure the concentrations of other species in solution. Some of the species whose concentrations can be determined in aqueous solution using ion-selective electrodes and similar devices are listed in Table 19.1 "Some Species Whose Aqueous Concentrations Can Be Measured Using Electrochemical Methods".
Table 19.1 Some Species Whose Aqueous Concentrations Can Be Measured Using Electrochemical Methods
| Species | Type of Sample |
|---|---|
| H+ | laboratory samples, blood, soil, and ground and surface water |
| NH3/NH4+ | wastewater and runoff water |
| K+ | blood, wine, and soil |
| CO2/HCO3− | blood and groundwater |
| F− | groundwater, drinking water, and soil |
| Br− | grains and plant extracts |
| I− | milk and pharmaceuticals |
| NO3− | groundwater, drinking water, soil, and fertilizer |
The flow of electrons in an electrochemical cell depends on the identity of the reacting substances, the difference in the potential energy of their valence electrons, and their concentrations. The potential of the cell under standard conditions (1 M for solutions, 1 atm for gases, pure solids or liquids for other substances) and at a fixed temperature (25°C) is called the standard cell potential (E°cell). Only the difference between the potentials of two electrodes can be measured. By convention, all tabulated values of standard electrode potentials are listed as standard reduction potentials. The overall cell potential is the reduction potential of the reductive half-reaction minus the reduction potential of the oxidative half-reaction (E°cell = E°cathode − E°anode). The potential of the standard hydrogen electrode (SHE) is defined as 0 V under standard conditions. The potential of a half-reaction measured against the SHE under standard conditions is called its standard electrode potential. The standard cell potential is a measure of the driving force for a given redox reaction. All E° values are independent of the stoichiometric coefficients for the half-reaction. Redox reactions can be balanced using the half-reaction method, in which the overall redox reaction is divided into an oxidation half-reaction and a reduction half-reaction, each balanced for mass and charge. The half-reactions selected from tabulated lists must exactly reflect reaction conditions. In an alternative method, the atoms in each half-reaction are balanced, and then the charges are balanced. Whenever a half-reaction is reversed, the sign of E° corresponding to that reaction must also be reversed. If E°cell is positive, the reaction will occur spontaneously under standard conditions. If E°cell is negative, then the reaction is not spontaneous under standard conditions, although it will proceed spontaneously in the opposite direction. The potential of an indicator electrode is related to the concentration of the substance being measured, whereas the potential of the reference electrode is held constant. Whether reduction or oxidation occurs depends on the potential of the sample versus the potential of the reference electrode. In addition to the SHE, other reference electrodes are the silver–silver chloride electrode; the saturated calomel electrode (SCE); the glass electrode, which is commonly used to measure pH; and ion-selective electrodes, which depend on the concentration of a single ionic species in solution. Differences in potential between the SHE and other reference electrodes must be included when calculating values for E°.
Is a hydrogen electrode chemically inert? What is the major disadvantage to using a hydrogen electrode?
List two factors that affect the measured potential of an electrochemical cell and explain their impact on the measurements.
What is the relationship between electron flow and the potential energy of valence electrons? If the valence electrons of substance A have a higher potential energy than those of substance B, what is the direction of electron flow between them in a galvanic cell?
If the components of a galvanic cell include aluminum and bromine, what is the predicted direction of electron flow? Why?
Write a cell diagram representing a cell that contains the Ni/Ni2+ couple in one compartment and the SHE in the other compartment. What are the values of E°cathode, E°anode, and E°cell?
Explain why E° values are independent of the stoichiometric coefficients in the corresponding half-reaction.
Identify the oxidants and the reductants in each redox reaction.
Identify the oxidants and the reductants in each redox reaction.
All reference electrodes must conform to certain requirements. List the requirements and explain their significance.
For each application, describe the reference electrode you would use and explain why. In each case, how would the measured potential compare with the corresponding E°?
Ni(s)∣Ni2+(aq)∥H+(aq, 1 M)∣H2(g, 1 atm)∣Pt(s)
Draw the cell diagram for a galvanic cell with an SHE and a copper electrode that carries out this overall reaction: H2(g) + Cu2+(aq) → 2H+(aq) + Cu(s).
Draw the cell diagram for a galvanic cell with an SHE and a zinc electrode that carries out this overall reaction: Zn(s) + 2H+(aq) → Zn2+(aq) + H2(g).
Balance each reaction and calculate the standard electrode potential for each. Be sure to include the physical state of each product and reactant.
Balance each reaction and calculate the standard reduction potential for each. Be sure to include the physical state of each product and reactant.
Write a balanced chemical equation for each redox reaction.
Write a balanced chemical equation for each redox reaction.
The standard cell potential for the oxidation of Pb to Pb2+ with the concomitant reduction of Cu+ to Cu is 0.39 V. You know that E° for the Pb2+/Pb couple is −0.13 V. What is E° for the Cu+/Cu couple?
You have built a galvanic cell similar to the one in Figure 19.7 "Determining a Standard Electrode Potential Using a Standard Hydrogen Electrode" using an iron nail, a solution of FeCl2, and an SHE. When the cell is connected, you notice that the iron nail begins to corrode. What else do you observe? Under standard conditions, what is Ecell?
Carbon is used to reduce iron ore to metallic iron. The overall reaction is as follows:
2Fe2O3·xH2O(s) + 3C(s) → 4Fe(l) + 3CO2(g) + 2xH2O(g)Write the two half-reactions for this overall reaction.
Will each reaction occur spontaneously under standard conditions?
Each reaction takes place in acidic solution. Balance each reaction and then determine whether it occurs spontaneously as written under standard conditions.
Calculate E°cell and ΔG° for the redox reaction represented by the cell diagram Pt(s)∣Cl2(g, 1 atm)∥ZnCl2(aq, 1 M)∣Zn(s). Will this reaction occur spontaneously?
If you place Zn-coated (galvanized) tacks in a glass and add an aqueous solution of iodine, the brown color of the iodine solution fades to a pale yellow. What has happened? Write the two half-reactions and the overall balanced chemical equation for this reaction. What is E°cell?
Your lab partner wants to recover solid silver from silver chloride by using a 1.0 M solution of HCl and 1 atm H2 under standard conditions. Will this plan work?
Pt(s)∣H2(g, 1 atm) | H+(aq, 1M)∥Cu2+(aq)∣Cu(s)