One of the most striking characteristics of transition-metal complexes is the wide range of colors they exhibit (Figure 23.4 "Aqueous Solutions of Vanadium Ions in Oxidation States of +2 to +5" and Figure 23.5 "Compounds of Manganese in Oxidation States +2 to +7"). In this section, we describe crystal field theory (CFT)A bonding model based on the assumption that metal–ligand interactions are purely electrostatic in nature, which explains many important properties of transition-metal complexes., a bonding model that explains many important properties of transition-metal complexes, including their colors, magnetism, structures, stability, and reactivity. The central assumption of CFT is that metal–ligand interactions are purely electrostatic in nature. Even though this assumption is clearly not valid for many complexes, such as those that contain neutral ligands like CO, CFT enables chemists to explain many of the properties of transition-metal complexes with a reasonable degree of accuracy.
CFT focuses on the interaction of the five (n − 1)d orbitals with ligands arranged in a regular array around a transition-metal ion. We will focus on the application of CFT to octahedral complexes, which are by far the most common and the easiest to visualize. Other common structures, such as square planar complexes, can be treated as a distortion of the octahedral model. According to CFT, an octahedral metal complex forms because of the electrostatic interaction of a positively charged metal ion with six negatively charged ligands or with the negative ends of dipoles associated with the six ligands. In addition, the ligands interact with one other electrostatically. As you learned in our discussion of the valence-shell electron-pair repulsion (VSEPR) model in Chapter 9 "Molecular Geometry and Covalent Bonding Models", the lowest-energy arrangement of six identical negative charges is an octahedron, which minimizes repulsive interactions between the ligands.
We begin by considering how the energies of the d orbitals of a transition-metal ion are affected by an octahedral arrangement of six negative charges. Recall from Chapter 6 "The Structure of Atoms" that the five d orbitals are initially degenerate (have the same energy). If we distribute six negative charges uniformly over the surface of a sphere, the d orbitals remain degenerate, but their energy will be higher due to repulsive electrostatic interactions between the spherical shell of negative charge and electrons in the d orbitals (part (a) in Figure 23.10 "An Octahedral Arrangement of Six Negative Charges around a Metal Ion Causes the Five "). Placing the six negative charges at the vertices of an octahedron does not change the average energy of the d orbitals, but it does remove their degeneracy: the five d orbitals split into two groups whose energies depend on their orientations. As shown in part (b) in Figure 23.10 "An Octahedral Arrangement of Six Negative Charges around a Metal Ion Causes the Five ", the and orbitals point directly at the six negative charges located on the x, y, and z axes. Consequently, the energy of an electron in these two orbitals (collectively labeled the eg orbitals) will be greater than it will be for a spherical distribution of negative charge because of increased electrostatic repulsions. In contrast, the other three d orbitals (dxy, dxz, and dyz, collectively called the t2g orbitals) are all oriented at a 45° angle to the coordinate axes, so they point between the six negative charges. The energy of an electron in any of these three orbitals is lower than the energy for a spherical distribution of negative charge.
Figure 23.10 An Octahedral Arrangement of Six Negative Charges around a Metal Ion Causes the Five d Orbitals to Split into Two Sets with Different Energies
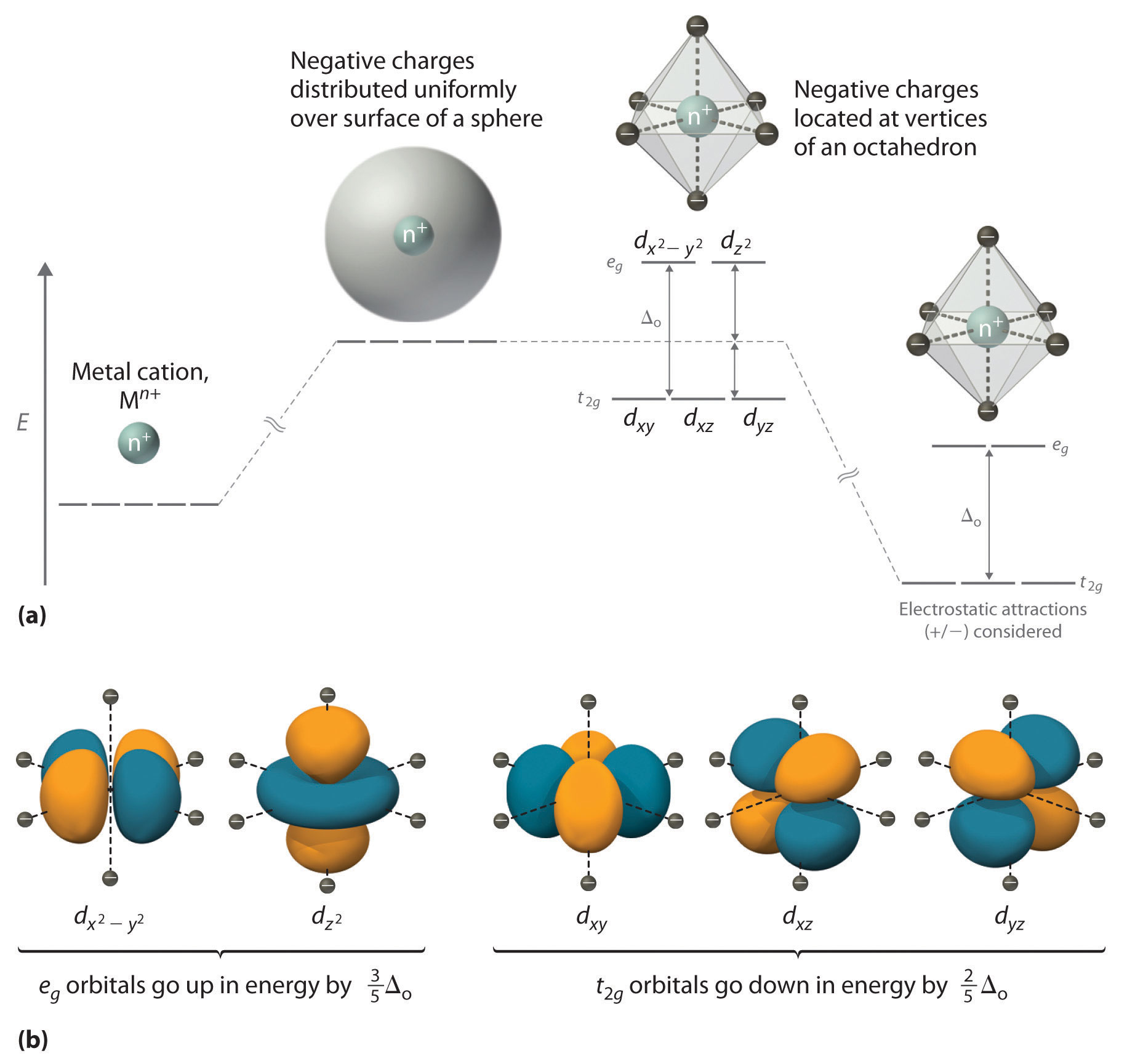
(a) Distributing a charge of −6 uniformly over a spherical surface surrounding a metal ion causes the energy of all five d orbitals to increase due to electrostatic repulsions, but the five d orbitals remain degenerate. Placing a charge of −1 at each vertex of an octahedron causes the d orbitals to split into two groups with different energies: the and orbitals increase in energy, while the, dxy, dxz, and dyz orbitals decrease in energy. The average energy of the five d orbitals is the same as for a spherical distribution of a −6 charge, however. Attractive electrostatic interactions between the negatively charged ligands and the positively charged metal ion (far right) cause all five d orbitals to decrease in energy but does not affect the splittings of the orbitals. (b) The two eg orbitals (left) point directly at the six negatively charged ligands, which increases their energy compared with a spherical distribution of negative charge. In contrast, the three t2g orbitals (right) point between the negatively charged ligands, which decreases their energy compared with a spherical distribution of charge.
The difference in energy between the two sets of d orbitals is called the crystal field splitting energyThe difference in energy between the set of orbitals and and the set of orbitals , , that results when the five orbitals are placed in an octahedral crystal field. (Δo), where the subscript o stands for octahedral. As we shall see, the magnitude of the splitting depends on the charge on the metal ion, the position of the metal in the periodic table, and the nature of the ligands. (Crystal field splitting energy also applies to tetrahedral complexes: Δt.) It is important to note that the splitting of the d orbitals in a crystal field does not change the total energy of the five d orbitals: the two eg orbitals increase in energy by 0.6Δo, whereas the three t2g orbitals decrease in energy by 0.4Δo. Thus the total change in energy is 2(0.6Δo) + 3(−0.4Δo) = 0.
Crystal field splitting does not change the total energy of the d orbitals.
Thus far, we have considered only the effect of repulsive electrostatic interactions between electrons in the d orbitals and the six negatively charged ligands, which increases the total energy of the system and splits the d orbitals. Interactions between the positively charged metal ion and the ligands results in a net stabilization of the system, which decreases the energy of all five d orbitals without affecting their splitting (as shown at the far right in part (a) in Figure 23.10 "An Octahedral Arrangement of Six Negative Charges around a Metal Ion Causes the Five ").
We can use the d-orbital energy-level diagram in Figure 23.10 "An Octahedral Arrangement of Six Negative Charges around a Metal Ion Causes the Five " to predict electronic structures and some of the properties of transition-metal complexes. We start with the Ti3+ ion, which contains a single d electron, and proceed across the first row of the transition metals by adding a single electron at a time. We place additional electrons in the lowest-energy orbital available, while keeping their spins parallel as required by Hund’s rule. As shown in Figure 23.11 "The Possible Electron Configurations for Octahedral ", for d1–d3 systems—such as [Ti(H2O)6]3+, [V(H2O)6]3+, and [Cr(H2O)6]3+, respectively—the electrons successively occupy the three degenerate t2g orbitals with their spins parallel, giving one, two, and three unpaired electrons, respectively. We can summarize this for the complex [Cr(H2O)6]3+, for example, by saying that the chromium ion has a d3 electron configuration or, more succinctly, Cr3+ is a d3 ion.
Figure 23.11 The Possible Electron Configurations for Octahedral dn Transition-Metal Complexes (n = 1–10)

Two different configurations are possible for octahedral complexes of metals with d4, d5, d6, and d7 configurations; the magnitude of Δo determines which configuration is observed.
When we reach the d4 configuration, there are two possible choices for the fourth electron: it can occupy either one of the empty eg orbitals or one of the singly occupied t2g orbitals. Recall from Chapter 6 "The Structure of Atoms" that placing an electron in an already occupied orbital results in electrostatic repulsions that increase the energy of the system; this increase in energy is called the spin-pairing energy (P)The energy that must be overcome to place an electron in an orbital that already has one electron.. If Δo is less than P, then the lowest-energy arrangement has the fourth electron in one of the empty eg orbitals. Because this arrangement results in four unpaired electrons, it is called a high-spin configuration, and a complex with this electron configuration, such as the [Cr(H2O)6]2+ ion, is called a high-spin complex. Conversely, if Δo is greater than P, then the lowest-energy arrangement has the fourth electron in one of the occupied t2g orbitals. Because this arrangement results in only two unpaired electrons, it is called a low-spin configuration, and a complex with this electron configuration, such as the [Mn(CN)6]3− ion, is called a low-spin complex. Similarly, metal ions with the d5, d6, or d7 electron configurations can be either high spin or low spin, depending on the magnitude of Δo.
In contrast, only one arrangement of d electrons is possible for metal ions with d8–d10 electron configurations. For example, the [Ni(H2O)6]2+ ion is d8 with two unpaired electrons, the [Cu(H2O)6]2+ ion is d9 with one unpaired electron, and the [Zn(H2O)6]2+ ion is d10 with no unpaired electrons.
If Δo is less than the spin-pairing energy, a high-spin configuration results. Conversely, if Δo is greater, a low-spin configuration forms.
The magnitude of Δo dictates whether a complex with four, five, six, or seven d electrons is high spin or low spin, which affects its magnetic properties, structure, and reactivity. Large values of Δo (i.e., Δo > P) yield a low-spin complex, whereas small values of Δo (i.e., Δo < P) produce a high-spin complex. As we noted, the magnitude of Δo depends on three factors: the charge on the metal ion, the principal quantum number of the metal (and thus its location in the periodic table), and the nature of the ligand. Values of Δo for some representative transition-metal complexes are given in Table 23.10 "Crystal Field Splitting Energies for Some Octahedral (Δ".
Table 23.10 Crystal Field Splitting Energies for Some Octahedral (Δo)* and Tetrahedral (Δt) Transition-Metal Complexes
| Octahedral Complexes | Δo (cm−1) | Octahedral Complexes | Δo (cm−1) | Tetrahedral Complexes | Δt (cm−1) |
|---|---|---|---|---|---|
| [Ti(H2O)6]3+ | 20,300 | [Fe(CN)6]4− | 32,800 | VCl4 | 9010 |
| [V(H2O)6]2+ | 12,600 | [Fe(CN)6]3− | 35,000 | [CoCl4]2− | 3300 |
| [V(H2O)6]3+ | 18,900 | [CoF6]3− | 13,000 | [CoBr4]2− | 2900 |
| [CrCl6]3− | 13,000 | [Co(H2O)6]2+ | 9300 | [CoI4]2− | 2700 |
| [Cr(H2O)6]2+ | 13,900 | [Co(H2O)6]3+ | 27,000 | ||
| [Cr(H2O)6]3+ | 17,400 | [Co(NH3)6]3+ | 22,900 | ||
| [Cr(NH3)6]3+ | 21,500 | [Co(CN)6]3− | 34,800 | ||
| [Cr(CN)6]3− | 26,600 | [Ni(H2O)6]2+ | 8500 | ||
| Cr(CO)6 | 34,150 | [Ni(NH3)6]2+ | 10,800 | ||
| [MnCl6]4− | 7500 | [RhCl6]3− | 20,400 | ||
| [Mn(H2O)6]2+ | 8500 | [Rh(H2O)6]3+ | 27,000 | ||
| [MnCl6]3− | 20,000 | [Rh(NH3)6]3+ | 34,000 | ||
| [Mn(H2O)6]3+ | 21,000 | [Rh(CN)6]3− | 45,500 | ||
| [Fe(H2O)6]2+ | 10,400 | [IrCl6]3− | 25,000 | ||
| [Fe(H2O)6]3+ | 14,300 | [Ir(NH3)6]3+ | 41,000 | ||
| *Energies obtained by spectroscopic measurements are often given in units of wave numbers (cm−1); the wave number is the reciprocal of the wavelength of the corresponding electromagnetic radiation expressed in centimeters: 1 cm−1 = 11.96 J/mol. | |||||
Source of data: Duward F. Shriver, Peter W. Atkins, and Cooper H. Langford, Inorganic Chemistry, 2nd ed. (New York: W. H. Freeman and Company, 1994).
Increasing the charge on a metal ion has two effects: the radius of the metal ion decreases, and negatively charged ligands are more strongly attracted to it. Both factors decrease the metal–ligand distance, which in turn causes the negatively charged ligands to interact more strongly with the d orbitals. Consequently, the magnitude of Δo increases as the charge on the metal ion increases. Typically, Δo for a tripositive ion is about 50% greater than for the dipositive ion of the same metal; for example, for [V(H2O)6]2+, Δo = 11,800 cm−1; for [V(H2O)6]3+, Δo = 17,850 cm−1.
For a series of complexes of metals from the same group in the periodic table with the same charge and the same ligands, the magnitude of Δo increases with increasing principal quantum number: Δo (3d) < Δo (4d) < Δo (5d). The data for hexaammine complexes of the trivalent group 9 metals illustrate this point:
The increase in Δo with increasing principal quantum number is due to the larger radius of valence orbitals down a column. In addition, repulsive ligand–ligand interactions are most important for smaller metal ions. Relatively speaking, this results in shorter M–L distances and stronger d orbital–ligand interactions.
Experimentally, it is found that the Δo observed for a series of complexes of the same metal ion depends strongly on the nature of the ligands. For a series of chemically similar ligands, the magnitude of Δo decreases as the size of the donor atom increases. For example, Δo values for halide complexes generally decrease in the order F− > Cl− > Br− > I− because smaller, more localized charges, such as we see for F−, interact more strongly with the d orbitals of the metal ion. In addition, a small neutral ligand with a highly localized lone pair, such as NH3, results in significantly larger Δo values than might be expected. Because the lone pair points directly at the metal ion, the electron density along the M–L axis is greater than for a spherical anion such as F−. The experimentally observed order of the crystal field splitting energies produced by different ligands is called the spectrochemical seriesAn ordering of ligands by their crystal field splitting energies., shown here in order of decreasing Δo:
The values of Δo listed in Table 23.10 "Crystal Field Splitting Energies for Some Octahedral (Δ" illustrate the effects of the charge on the metal ion, the principal quantum number of the metal, and the nature of the ligand.
The largest Δos are found in complexes of metal ions from the third row of the transition metals with charges of at least +3 and ligands with localized lone pairs of electrons.
The striking colors exhibited by transition-metal complexes are caused by excitation of an electron from a lower-energy d orbital to a higher-energy d orbital, which is called a d–d transition (Figure 23.12 "A "). For a photon to effect such a transition, its energy must be equal to the difference in energy between the two d orbitals, which depends on the magnitude of Δo.
Figure 23.12 A d–d Transition

In a d–d transition, an electron in one of the t2g orbitals of an octahedral complex such as the [Cr(H2O)6]3+ ion absorbs a photon of light with energy equal to Δo, which causes the electron to move to an empty or singly occupied eg orbital.
Recall from Chapter 6 "The Structure of Atoms" that the color we observe when we look at an object or a compound is due to light that is transmitted or reflected, not light that is absorbed, and that reflected or transmitted light is complementary in color to the light that is absorbed. Thus a green compound absorbs light in the red portion of the visible spectrum and vice versa, as indicated by the color wheel in End-of-Chapter Application Problem 6 in Chapter 6 "The Structure of Atoms". Because the energy of a photon of light is inversely proportional to its wavelength, the color of a complex depends on the magnitude of Δo, which depends on the structure of the complex. For example, the complex [Cr(NH3)6]3+ has strong-field ligands and a relatively large Δo. Consequently, it absorbs relatively high-energy photons, corresponding to blue-violet light, which gives it a yellow color. A related complex with weak-field ligands, the [Cr(H2O)6]3+ ion, absorbs lower-energy photons corresponding to the yellow-green portion of the visible spectrum, giving it a deep violet color.
We can now understand why emeralds and rubies have such different colors, even though both contain Cr3+ in an octahedral environment provided by six oxide ions. Although the chemical identity of the six ligands is the same in both cases, the Cr–O distances are different because the compositions of the host lattices are different (Al2O3 in rubies and Be3Al2Si6O18 in emeralds). In ruby, the Cr–O distances are relatively short because of the constraints of the host lattice, which increases the d orbital–ligand interactions and makes Δo relatively large. Consequently, rubies absorb green light and the transmitted or reflected light is red, which gives the gem its characteristic color. In emerald, the Cr–O distances are longer due to relatively large [Si6O18]12− silicate rings; this results in decreased d orbital–ligand interactions and a smaller Δo. Consequently, emeralds absorb light of a longer wavelength (red), which gives the gem its characteristic green color. It is clear that the environment of the transition-metal ion, which is determined by the host lattice, dramatically affects the spectroscopic properties of a metal ion.

Gem-quality crystals of ruby and emerald. The colors of both minerals are due to the presence of small amounts of Cr3+ impurities in octahedral sites in an otherwise colorless metal oxide lattice.
Recall from Chapter 9 "Molecular Geometry and Covalent Bonding Models" that stable molecules contain more electrons in the lower-energy (bonding) molecular orbitals in a molecular orbital diagram than in the higher-energy (antibonding) molecular orbitals. If the lower-energy set of d orbitals (the t2g orbitals) is selectively populated by electrons, then the stability of the complex increases. For example, the single d electron in a d1 complex such as [Ti(H2O)6]3+ is located in one of the t2g orbitals. Consequently, this complex will be more stable than expected on purely electrostatic grounds by 0.4Δo. The additional stabilization of a metal complex by selective population of the lower-energy d orbitals is called its crystal field stabilization energy (CFSE)The additional stabilization of a metal complex by selective population of the lower-energy orbitals (the t2g orbitals).. The CFSE of a complex can be calculated by multiplying the number of electrons in t2g orbitals by the energy of those orbitals (−0.4Δo), multiplying the number of electrons in eg orbitals by the energy of those orbitals (+0.6Δo), and summing the two. Table 23.11 "CFSEs for Octahedral Complexes with Different Electron Configurations (in Units of Δ" gives CFSE values for octahedral complexes with different d electron configurations. The CFSE is highest for low-spin d6 complexes, which accounts in part for the extraordinarily large number of Co(III) complexes known. The other low-spin configurations also have high CFSEs, as does the d3 configuration.
Table 23.11 CFSEs for Octahedral Complexes with Different Electron Configurations (in Units of Δo)
| High Spin | CFSE (Δo) | Low Spin | CFSE (Δo) | |||
|---|---|---|---|---|---|---|
| d 0 | 0 | |||||
| d 1 | ↿ | 0.4 | ||||
| d 2 | ↿ ↿ | 0.8 | ||||
| d 3 | ↿ ↿ ↿ | 1.2 | ||||
| d 4 | ↿ ↿ ↿ | ↿ | 0.6 | ↿⇂ ↿ ↿ | 1.6 | |
| d 5 | ↿ ↿ ↿ | ↿ ↿ | 0.0 | ↿⇂ ↿⇂ ↿ | 2.0 | |
| d 6 | ↿⇂ ↿ ↿ | ↿ ↿ | 0.4 | ↿⇂ ↿⇂ ↿⇂ | 2.4 | |
| d 7 | ↿⇂ ↿⇂ ↿ | ↿ ↿ | 0.8 | ↿⇂ ↿⇂ ↿⇂ | ↿ | 1.8 |
| d 8 | ↿⇂ ↿⇂ ↿⇂ | ↿ ↿ | 1.2 | |||
| d 9 | ↿⇂ ↿⇂ ↿⇂ | ↿⇂ ↿ | 0.6 | |||
| d 10 | ↿⇂ ↿⇂ ↿⇂ | ↿⇂ ↿⇂ | 0.0 | |||
CFSEs are important for two reasons. First, the existence of CFSE nicely accounts for the difference between experimentally measured values for bond energies in metal complexes and values calculated based solely on electrostatic interactions. Second, CFSEs represent relatively large amounts of energy (up to several hundred kilojoules per mole), which has important chemical consequences.
Octahedral d3 and d8 complexes and low-spin d6, d5, d7, and d4 complexes exhibit large CFSEs.
If two trans ligands in an octahedral complex are either chemically different from the other four, as in the trans-[Co(NH3)4Cl2]+ ion, or at a different distance from the metal than the other four, the result is a tetragonally distorted octahedral complex. The electronic structures of such complexes are best viewed as the result of distorting an octahedral complex. Consider, for example, an octahedral complex such as [Co(NH3)6]3+ and then slowly remove two trans NH3 molecules by moving them away from the metal along the ±z axes, as shown in the top half of Figure 23.13. As the two axial Co–N distances increase simultaneously, the d orbitals that interact most strongly with the two axial ligands will decrease in energy due to a decrease in electrostatic repulsions between electrons in these orbitals and the negative ends of the ligand dipoles. The affected d orbitals are those with a component along the ±z axes—namely, , dxz, and dyz. They will not be affected equally, however. Because the orbital points directly at the two ligands being removed, its energy will decrease much more rapidly than the energy of the other two, as shown in the bottom half of Figure 23.13. In addition, the positive charge on the metal will increase somewhat as the axial ligands are removed, causing the four remaining in-plane ligands to be more strongly attracted to the metal. This will increase their interactions with the other two d orbitals and increase their energy. Again, the two d orbitals will not be affected equally. Because the orbital points directly at the four in-plane ligands, its energy will increase more rapidly than the energy of the dxy orbital, which points between the in-plane ligands. If we remove the two axial ligands to an infinite distance, we obtain a square planar complex. The energies of the and dxy orbitals actually cross as the axial ligands are removed, and the largest orbital spliting in a square planar complex is identical in magnitude to Δo.
Figure 23.13 d-Orbital Splittings for Tetragonal and Square Planar Complexes
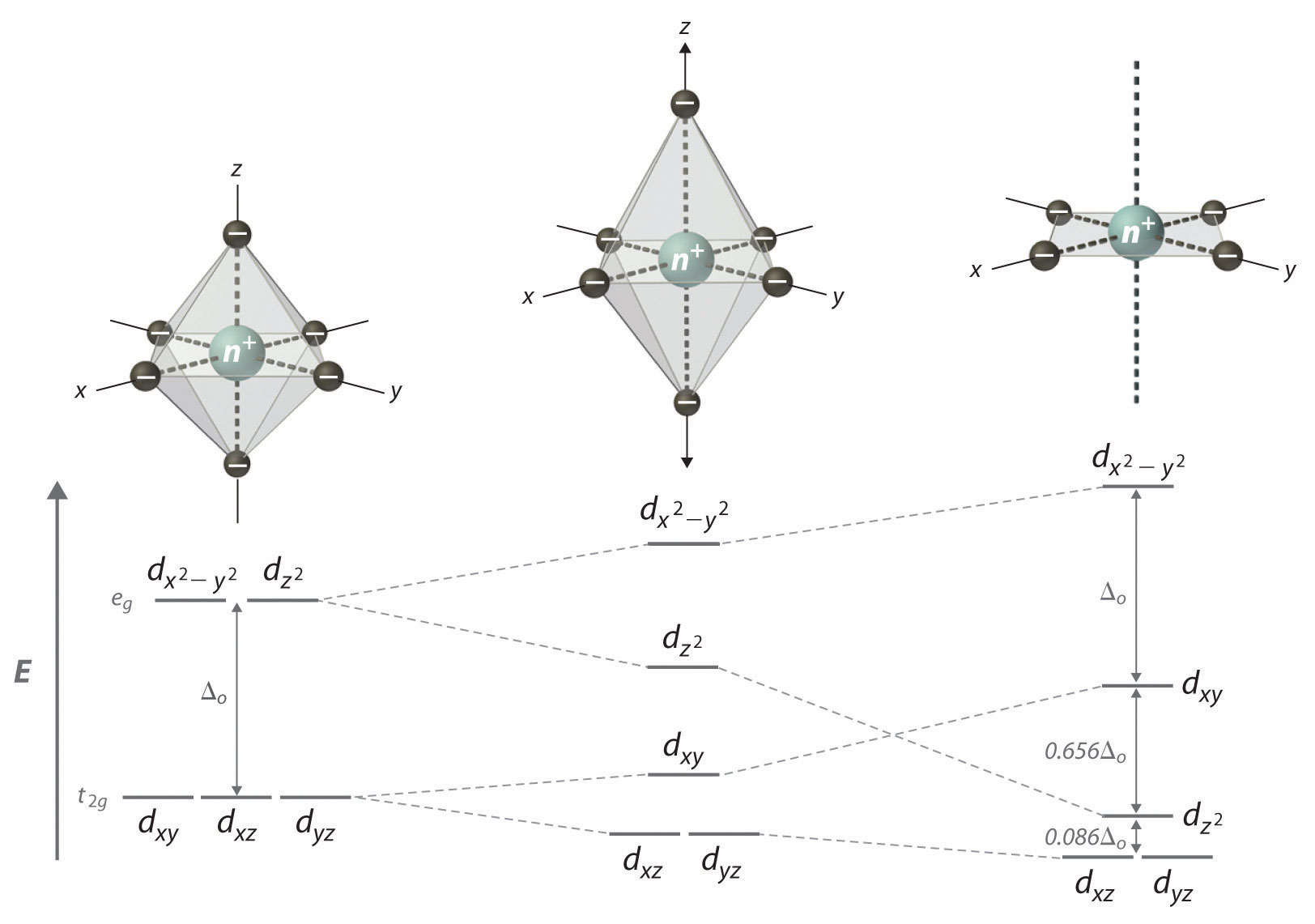
Moving the two axial ligands away from the metal ion along the z axis initially gives an elongated octahedral complex (center) and eventually produces a square planar complex (right). As shown below the structures, an axial elongation causes the dxz and dyz orbitals to decrease in energy and the and dxy orbitals to increase in energy. As explained in the text, the change in energy is not the same for all five d orbitals. Removing the two axial ligands completely causes the energy of the orbital to decrease so much that the order of the and dxy orbitals is reversed.
In a tetrahedral arrangement of four ligands around a metal ion, none of the ligands lies on any of the three coordinate axes (part (a) in Figure 23.14); consequently, none of the five d orbitals points directly at the ligands. Nonetheless, the dxy, dxz, and dyz orbitals interact more strongly with the ligands than do and again resulting in a splitting of the five d orbitals into two sets. The splitting of the energies of the orbitals in a tetrahedral complex (Δt) is much smaller than that for Δo, however, for two reasons. First, the d orbitals interact less strongly with the ligands in a tetrahedral arrangement. Second, there are only four negative charges rather than six, which decreases the electrostatic interactions by one-third if all other factors are equal. It can be shown that, for complexes of the same metal ion with the same charge, the same ligands, and the same M–L distance, The relationship between the splitting of the five d orbitals in octahedral and tetrahedral crystal fields imposed by the same ligands is shown schematically in part (b) in Figure 23.14.
Figure 23.14 d-Orbital Splittings for a Tetrahedral Complex

(a) In a tetrahedral complex, none of the five d orbitals points directly at or between the ligands. (b) Because the dxy, dxz, and dyz orbitals (the t2g orbitals) interact more strongly with the ligands than do the and orbitals (the eg orbitals), the order of orbital energies in a tetrahedral complex is the opposite of the order in an octahedral complex.
Δt < Δo because of weaker d-orbital–ligand interactions and decreased electrostatic interactions.
Because Δo is so large for the second- and third-row transition metals, all four-coordinate complexes of these metals are square planar due to the much higher CFSE for square planar versus tetrahedral structures. The only exception is for d10 metal ions such as Cd2+, which have zero CFSE and are therefore tetrahedral as predicted by the VSEPR model. Four-coordinate complexes of the first-row transition metals can be either square planar or tetrahedral. The former is favored by strong-field ligands, whereas the latter is favored by weak-field ligands. For example, the [Ni(CN)4]2− ion is square planar, while the [NiCl4]2− ion is tetrahedral.
For each complex, predict its structure, whether it is high spin or low spin, and the number of unpaired electrons present.
Given: complexes
Asked for: structure, high spin versus low spin, and the number of unpaired electrons
Strategy:
A From the number of ligands, determine the coordination number of the compound.
B Classify the ligands as either strong field or weak field and determine the electron configuration of the metal ion.
C Predict the relative magnitude of Δo and decide whether the compound is high spin or low spin.
D Place the appropriate number of electrons in the d orbitals and determine the number of unpaired electrons.
Solution:
A With six ligands, we expect this complex to be octahedral.
B The fluoride ion is a small anion with a concentrated negative charge, but compared with ligands with localized lone pairs of electrons, it is weak field. The charge on the metal ion is +3, giving a d6 electron configuration.
C Because of the weak-field ligands, we expect a relatively small Δo, making the compound high spin.
D In a high-spin octahedral d6 complex, the first five electrons are placed individually in each of the d orbitals with their spins parallel, and the sixth electron is paired in one of the t2g orbitals, giving four unpaired electrons.
A This complex has four ligands, so it is either square planar or tetrahedral.
B C Because rhodium is a second-row transition metal ion with a d8 electron configuration and CO is a strong-field ligand, the complex is likely to be square planar with a large Δo, making it low spin. Because the strongest d-orbital interactions are along the x and y axes, the orbital energies increase in the order dyz, and dxz (these are degenerate); dxy; and
D The eight electrons occupy the first four of these orbitals, leaving the orbital empty. Thus there are no unpaired electrons.
Exercise
For each complex, predict its structure, whether it is high spin or low spin, and the number of unpaired electrons present.
Answer:
The splitting of the d orbitals because of their interaction with the ligands in a complex has important consequences for the chemistry of transition-metal complexes; they can be divided into structural effects and thermodynamic effects. Although the two kinds of effects are interrelated, we will consider them separately.
There are two major kinds of structural effects: effects on the ionic radius of metal ions with regular octahedral or tetrahedral geometries, and structural distortions that are observed for specific electron configurations.
Figure 23.15 "The Effect of " is a plot of the ionic radii of the divalent fourth-period metal ions versus atomic number. Only Ca2+(d0), Mn2+ (high-spin d5), and Zn2+ (d10) fall on the smooth curve calculated based on the effective nuclear charge (Zeff), which assumes that the distribution of d electrons is spherically symmetrical. All the other divalent ions fall below this curve because they have asymmetrical distributions of d electrons. (The points shown for Cr2+ and Cu2+ are only estimated values; as you will learn shortly, these two ions do not form any truly octahedral complexes.) To see why an asymmetrical distribution of d electrons makes a metal ion smaller than expected, consider the Ti2+ ion, which has a d2 configuration with both electrons in the t2g orbitals. Because the t2g orbitals are directed between the ligands, the two d electrons are unable to shield the ligands from the nuclear charge. Consequently, the ligands experience a higher effective nuclear charge than expected, the metal–ligand distance is unusually short, and the ionic radius is smaller than expected. If instead the two electrons were distributed uniformly over all five d orbitals, they would be much more effective at screening the ligands from the nuclear charge, making the metal–ligand distances longer and giving a larger ionic radius.
Figure 23.15 The Effect of d-Orbital Splittings on the Radii of the Divalent Ions of the Fourth-Period Metals

Because these radii are based on the structures of octahedral complexes and Cr2+ and Cu2+ do not form truly octahedral complexes, the points for these ions are shown as open circles. The dashed line represents the behavior predicted based on the effects of screening and variation in effective nuclear charge (Zeff), assuming a spherical distribution of the 3d electrons.
A similar effect is observed for the V2+ ion, which has a d3 configuration. Because the three electrons in the t2g orbitals provide essentially no shielding of the ligands from the metal, the ligands experience the full increase of +1 in nuclear charge that occurs in going from Ti2+ to V2+. Consequently, the observed ionic radius of the V2+ ion is significantly smaller than that of the Ti2+ ion.
Skipping the Cr2+ ion for the moment, we next consider the d5 Mn2+ ion. Because the nuclear charge increases by +2 from V2+ to Mn2+, we might expect Mn2+ to be smaller than V2+. The two electrons that are also added from V2+ to Mn2+ occupy the eg orbitals, however, which point directly at the six ligands. Because these electrons are localized directly between the metal ion and the ligands, they are effective at screening the ligands from the increased nuclear charge. As a result, the ionic radius actually increases significantly as we go from V2+ to Mn2+, despite the higher nuclear charge of the latter.
Exactly the same effects are seen in the second half of the first-row transition metals. In the Fe2+, Co2+, and Ni2+ ions, the extra electrons are added successively to the t2g orbitals, resulting in poor shielding of the ligands from the nuclear charge and abnormally small ionic radii. Skipping over Cu2+, we again see that adding the last two electrons causes a significant increase in the ionic radius of Zn2+, despite its higher nuclear charge.
Because simple octahedral complexes are not known for the Cr2+ and Cu2+ ions, only estimated values for their radii are shown in Figure 23.15 "The Effect of ". We see in Figure 23.11 "The Possible Electron Configurations for Octahedral " that both the Cr2+ and Cu2+ ions have electron configurations with an odd number of electrons in the eg orbitals. Because the single electron (in the case of Cr2+) or the third electron (in the case of Cu2+) can occupy either one of two degenerate eg orbitals, they have what is called a degenerate ground state. The Jahn–Teller theoremA theory that states that a non-linear molecule with a spatially degenerate electronic ground state will undergo a geometrical distortion to remove the degeneracy and lower the overall energy of the system. states that such non-linear systems are not stable; they will undergo a distortion that makes the complex less symmetrical and splits the degenerate states, which decreases the energy of the system. The distortion and resulting decrease in energy are collectively referred to as the Jahn–Teller effect. Neither the nature of the distortion nor its magnitude is specified, and in fact, they are difficult to predict. In principle, Jahn–Teller distortions are possible for many transition-metal ions; in practice, however, they are observed only for systems with an odd number of electrons in the eg orbitals, such as the Cr2+ and Cu2+ ions.
To see how a geometrical distortion can decrease the energy of such a system, consider an octahedral Cu2+ complex, the [Cu(H2O)6]2+ ion, which has been elongated along the z axis. As indicated in Figure 23.16 "The Jahn–Teller Effect", this kind of distortion splits both the eg and t2g sets of orbitals. Because the axial ligands interact most strongly with the orbital, the splitting of the eg set (δ1) is significantly larger than the splitting of the t2g set (δ2), but both δ1 and δ2 are much, much smaller than the Δo. This splitting does not change the center of gravity of the energy within each set, so a Jahn–Teller distortion results in no net change in energy for a filled or half-filled set of orbitals. If, however, the eg set contains one (as in the d4 ions, Cr2+ and Mn3+) or three (as in the d9 ion, Cu2+) electrons, the distortion decreases the energy of the system. For Cu2+, for example, the change in energy after distortion is 2(−δ1/2) + 1(δ1/2) = −δ1/2. For Cu2+ complexes, the observed distortion is always an elongation along the z axis by as much as 50 pm; in fact, many Cu2+ complexes are so distorted that they are effectively square planar. In contrast, the distortion observed for most Cr2+ complexes is a compression along the z axis. In both cases, however, the net effect is the same: the distorted system is more stable than the undistorted system.
Jahn–Teller distortions are most important for d9 and high-spin d4 complexes; the distorted system is more stable than the undistorted one.
Figure 23.16 The Jahn–Teller Effect
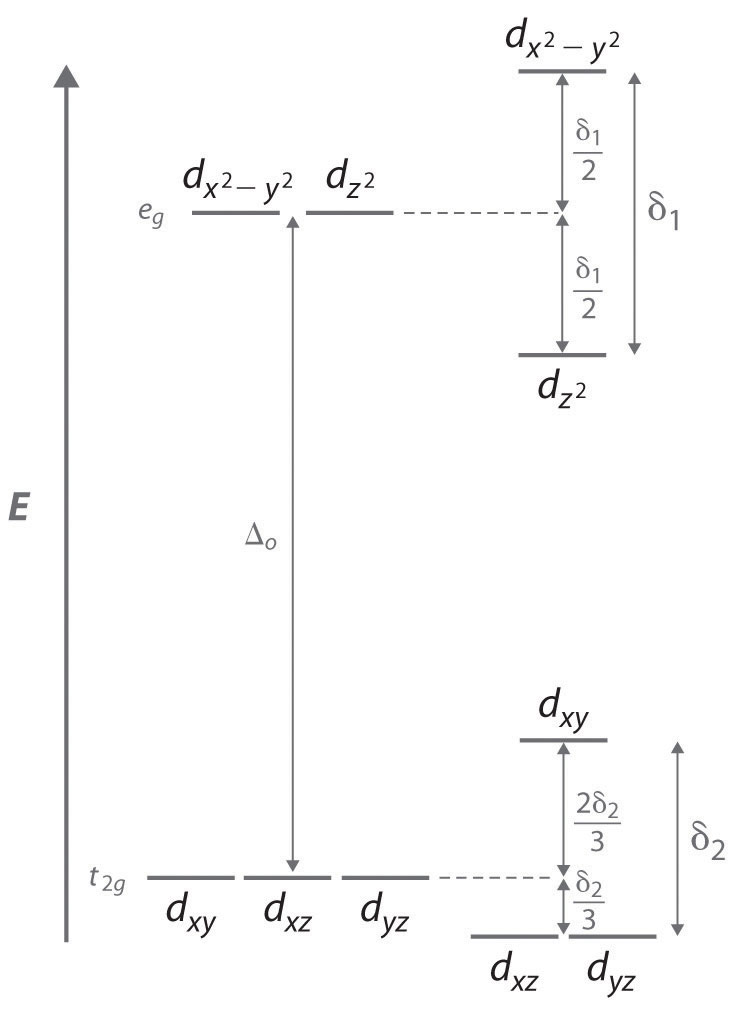
Increasing the axial metal–ligand distances in an octahedral d9 complex is an example of a Jahn–Teller distortion, which causes the degenerate pair of eg orbitals to split in energy by an amount δ1; δ1 and δ2 are much smaller than Δo. As a result, the distorted system is more stable (lower in energy) than the undistorted complex by δ1/2.
As we previously noted, CFSEs can be as large as several hundred kilojoules per mole, which is the same magnitude as the strength of many chemical bonds or the energy change in most chemical reactions. Consequently, CFSEs are important factors in determining the magnitude of hydration energies, lattice energies, and other thermodynamic properties of the transition metals.
The hydration energy of a metal ion is defined as the change in enthalpy for the following reaction:
Equation 23.12
M2+(g) + H2O(l) → M2+(aq)Although hydration energies cannot be measured directly, they can be calculated from experimentally measured quantities using thermochemical cycles. As shown in part (a) in Figure 23.17 "Thermochemical Effects of ", a plot of the hydration energies of the fourth-period metal dications versus atomic number gives a curve with two valleys. Note the relationship between the plot in part (a) in Figure 23.17 "Thermochemical Effects of " and the plot of ionic radii in Figure 23.15 "The Effect of ": the overall shapes are essentially identical, and only the three cations with spherically symmetrical distributions of d electrons (Ca2+, Mn2+, and Zn2+) lie on the dashed lines. In part (a) in Figure 23.17 "Thermochemical Effects of ", the dashed line corresponds to hydration energies calculated based solely on electrostatic interactions. Subtracting the CFSE values for the [M(H2O)6]2+ ions from the experimentally determined hydration energies gives the points shown as open circles, which lie very near the calculated curve. Thus CFSEs are primarily responsible for the differences between the measured and calculated values of hydration energies.
Figure 23.17 Thermochemical Effects of d-Orbital Splittings
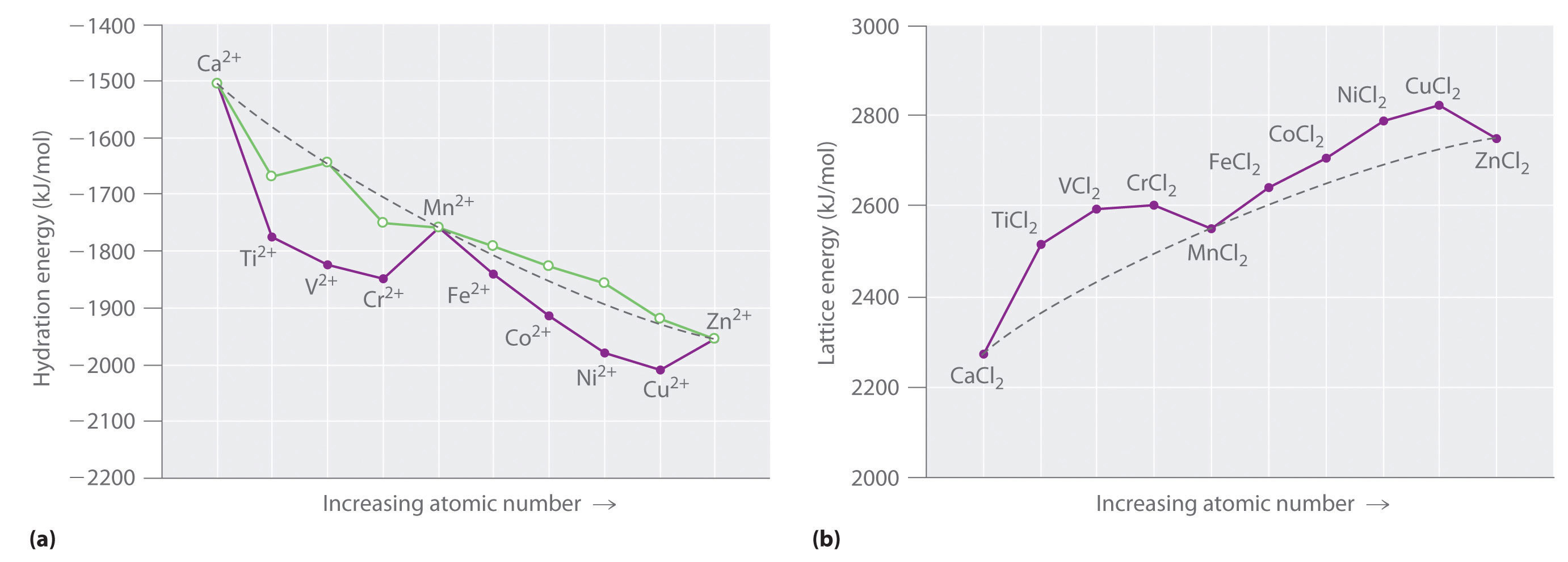
(a) A plot of the hydration energies of the divalent fourth-period metal ions versus atomic number (solid circles) shows large deviations from the smooth curve calculated, assuming a spherical distribution of d electrons (dashed line). Correcting for CFSE gives the points shown as open circles, which, except for Ti2+ and Cr2+, are close to the calculated values. The apparent deviations for these ions are caused by the fact that solutions of the Ti2+ ion in water are not stable, and Cr2+ does not form truly octahedral complexes. (b) A plot of the lattice energies for the fourth-period metal dichlorides versus atomic number shows similar deviations from the smooth curve calculated, assuming a spherical distribution of d electrons (dashed lines), again illustrating the importance of CFSEs.
Values of the lattice energies for the fourth-period metal dichlorides are plotted versus atomic number in part (b) in Figure 23.17 "Thermochemical Effects of ". Recall that the lattice energy is defined as the negative of the enthalpy change for the following reaction. Like hydration energies, lattice energies are determined indirectly by using a thermochemical cycle:
Equation 23.13
M2+(g) + 2Cl−(g) → MCl2(s)The shape of the lattice-energy curve is essentially the mirror image of the hydration-energy curve in part (a) in Figure 23.19 "Ferritin, an Iron Storage Protein", with only Ca2+, Mn2+, and Zn2+ lying on the smooth curve. It is not surprising that the explanation for the deviations from the curve is exactly the same as for the hydration energy data: all the transition-metal dichlorides, except MnCl2 and ZnCl2, are more stable than expected due to CFSE.
Crystal field theory (CFT) is a bonding model that explains many properties of transition metals that cannot be explained using valence bond theory. In CFT, complex formation is assumed to be due to electrostatic interactions between a central metal ion and a set of negatively charged ligands or ligand dipoles arranged around the metal ion. Depending on the arrangement of the ligands, the d orbitals split into sets of orbitals with different energies. The difference between the energy levels in an octahedral complex is called the crystal field splitting energy (Δo), whose magnitude depends on the charge on the metal ion, the position of the metal in the periodic table, and the nature of the ligands. The spin-pairing energy (P) is the increase in energy that occurs when an electron is added to an already occupied orbital. A high-spin configuration occurs when the Δo is less than P, which produces complexes with the maximum number of unpaired electrons possible. Conversely, a low-spin configuration occurs when the Δo is greater than P, which produces complexes with the minimum number of unpaired electrons possible. Strong-field ligands interact strongly with the d orbitals of the metal ions and give a large Δo, whereas weak-field ligands interact more weakly and give a smaller Δo. The colors of transition-metal complexes depend on the environment of the metal ion and can be explained by CFT. Distorting an octahedral complex by moving opposite ligands away from the metal produces a tetragonal or square planar arrangement, in which interactions with equatorial ligands become stronger. Because none of the d orbitals points directly at the ligands in a tetrahedral complex, these complexes have smaller values of the crystal field splitting energy Δt. The crystal field stabilization energy (CFSE) is the additional stabilization of a complex due to placing electrons in the lower-energy set of d orbitals. CFSE explains the unusual curves seen in plots of ionic radii, hydration energies, and lattice energies versus atomic number. The Jahn–Teller theorem states that a non-linear molecule with a spatially degenerate electronic ground state will undergo a geometrical distortion to remove the degeneracy and lower the overall energy of the system.
Describe crystal field theory in terms of its
In CFT, what causes degenerate sets of d orbitals to split into different energy levels? What is this splitting called? On what does the magnitude of the splitting depend?
Will the value of Δo increase or decrease if I− ligands are replaced by NO2− ligands? Why?
For an octahedral complex of a metal ion with a d6 configuration, what factors favor a high-spin configuration versus a low-spin configuration?
How can CFT explain the color of a transition-metal complex?
Do strong-field ligands favor a tetrahedral or a square planar structure? Why?
For each complex, predict its structure, whether it is high spin or low spin, and the number of unpaired electrons present.
For each complex, predict its structure, whether it is high spin or low spin, and the number of unpaired electrons present.
The ionic radii of V2+, Fe2+, and Zn2+ are all roughly the same (approximately 76 pm). Given their positions in the periodic table, explain why their ionic radii are so similar.