Often sampling is done in order to estimate the proportion of a population that has a specific characteristic, such as the proportion of all items coming off an assembly line that are defective or the proportion of all people entering a retail store who make a purchase before leaving. The population proportion is denoted p and the sample proportion is denoted Thus if in reality 43% of people entering a store make a purchase before leaving, p = 0.43; if in a sample of 200 people entering the store, 78 make a purchase,
The sample proportion is a random variable: it varies from sample to sample in a way that cannot be predicted with certainty. Viewed as a random variable it will be written It has a meanThe number about which proportions computed from samples of the same size center. and a standard deviationA measure of the variability of proportions computed from samples of the same size. Here are formulas for their values.
Suppose random samples of size n are drawn from a population in which the proportion with a characteristic of interest is p. The mean and standard deviation of the sample proportion satisfy
where
The Central Limit Theorem has an analogue for the population proportion To see how, imagine that every element of the population that has the characteristic of interest is labeled with a 1, and that every element that does not is labeled with a 0. This gives a numerical population consisting entirely of zeros and ones. Clearly the proportion of the population with the special characteristic is the proportion of the numerical population that are ones; in symbols,
But of course the sum of all the zeros and ones is simply the number of ones, so the mean μ of the numerical population is
Thus the population proportion p is the same as the mean μ of the corresponding population of zeros and ones. In the same way the sample proportion is the same as the sample mean Thus the Central Limit Theorem applies to However, the condition that the sample be large is a little more complicated than just being of size at least 30.
For large samples, the sample proportion is approximately normally distributed, with mean and standard deviation
A sample is large if the interval lies wholly within the interval
In actual practice p is not known, hence neither is In that case in order to check that the sample is sufficiently large we substitute the known quantity for p. This means checking that the interval
lies wholly within the interval This is illustrated in the examples.
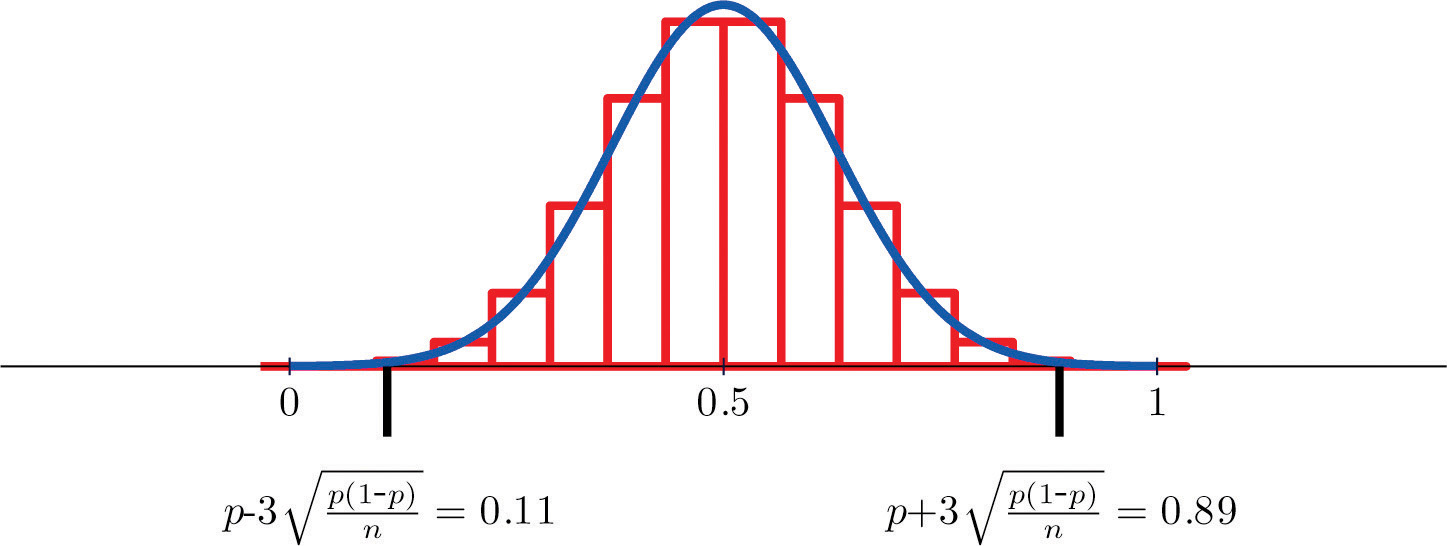
Figure 6.5 "Distribution of Sample Proportions" shows that when p = 0.1 a sample of size 15 is too small but a sample of size 100 is acceptable. Figure 6.6 "Distribution of Sample Proportions for " shows that when p = 0.5 a sample of size 15 is acceptable.
Figure 6.5 Distribution of Sample Proportions
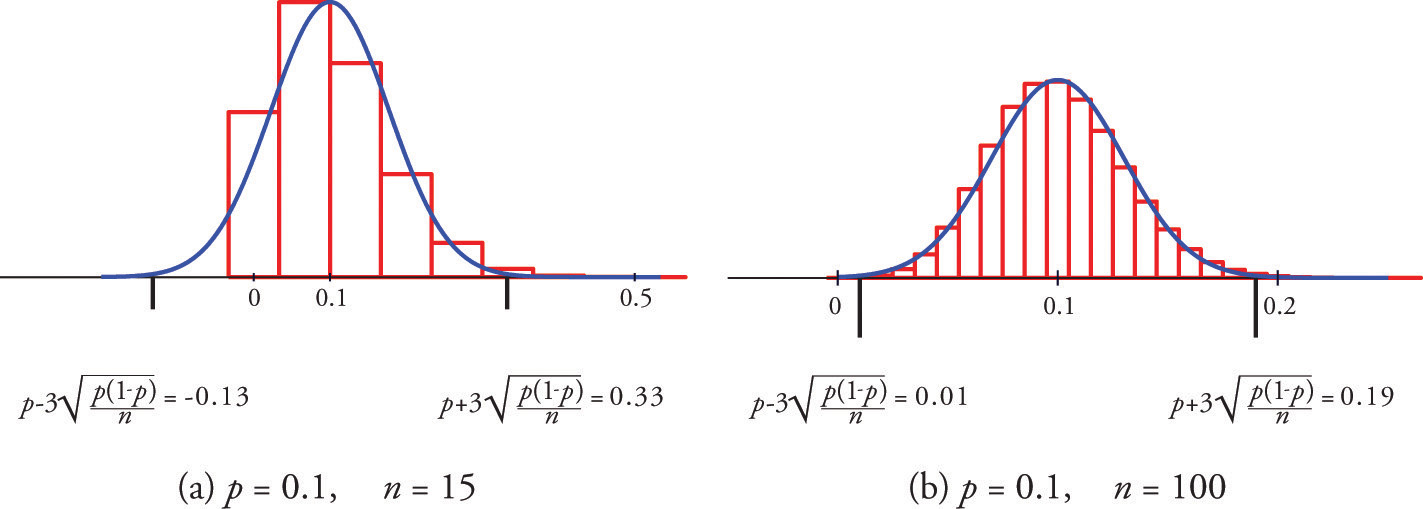
Figure 6.6 Distribution of Sample Proportions for p = 0.5 and n = 15
Suppose that in a population of voters in a certain region 38% are in favor of particular bond issue. Nine hundred randomly selected voters are asked if they favor the bond issue.
Solution
The information given is that p = 0.38, hence First we use the formulas to compute the mean and standard deviation of :
Then so
which lies wholly within the interval , so it is safe to assume that is approximately normally distributed.
To be within 5 percentage points of the true population proportion 0.38 means to be between and Thus
An online retailer claims that 90% of all orders are shipped within 12 hours of being received. A consumer group placed 121 orders of different sizes and at different times of day; 102 orders were shipped within 12 hours.
Solution
The sample proportion is the number x of orders that are shipped within 12 hours divided by the number n of orders in the sample:
Since p = 0.90, , and n = 121,
hence
Because it is appropriate to use the normal distribution to compute probabilities related to the sample proportion
Using the value of from part (a) and the computation in part (b),
The proportion of a population with a characteristic of interest is p = 0.37. Find the mean and standard deviation of the sample proportion obtained from random samples of size 1,600.
The proportion of a population with a characteristic of interest is p = 0.82. Find the mean and standard deviation of the sample proportion obtained from random samples of size 900.
The proportion of a population with a characteristic of interest is p = 0.76. Find the mean and standard deviation of the sample proportion obtained from random samples of size 1,200.
The proportion of a population with a characteristic of interest is p = 0.37. Find the mean and standard deviation of the sample proportion obtained from random samples of size 125.
Random samples of size 225 are drawn from a population in which the proportion with the characteristic of interest is 0.25. Decide whether or not the sample size is large enough to assume that the sample proportion is normally distributed.
Random samples of size 1,600 are drawn from a population in which the proportion with the characteristic of interest is 0.05. Decide whether or not the sample size is large enough to assume that the sample proportion is normally distributed.
Random samples of size n produced sample proportions as shown. In each case decide whether or not the sample size is large enough to assume that the sample proportion is normally distributed.
Samples of size n produced sample proportions as shown. In each case decide whether or not the sample size is large enough to assume that the sample proportion is normally distributed.
A random sample of size 121 is taken from a population in which the proportion with the characteristic of interest is p = 0.47. Find the indicated probabilities.
A random sample of size 225 is taken from a population in which the proportion with the characteristic of interest is p = 0.34. Find the indicated probabilities.
A random sample of size 900 is taken from a population in which the proportion with the characteristic of interest is p = 0.62. Find the indicated probabilities.
A random sample of size 1,100 is taken from a population in which the proportion with the characteristic of interest is p = 0.28. Find the indicated probabilities.
Suppose that 8% of all males suffer some form of color blindness. Find the probability that in a random sample of 250 men at least 10% will suffer some form of color blindness. First verify that the sample is sufficiently large to use the normal distribution.
Suppose that 29% of all residents of a community favor annexation by a nearby municipality. Find the probability that in a random sample of 50 residents at least 35% will favor annexation. First verify that the sample is sufficiently large to use the normal distribution.
Suppose that 2% of all cell phone connections by a certain provider are dropped. Find the probability that in a random sample of 1,500 calls at most 40 will be dropped. First verify that the sample is sufficiently large to use the normal distribution.
Suppose that in 20% of all traffic accidents involving an injury, driver distraction in some form (for example, changing a radio station or texting) is a factor. Find the probability that in a random sample of 275 such accidents between 15% and 25% involve driver distraction in some form. First verify that the sample is sufficiently large to use the normal distribution.
An airline claims that 72% of all its flights to a certain region arrive on time. In a random sample of 30 recent arrivals, 19 were on time. You may assume that the normal distribution applies.
A humane society reports that 19% of all pet dogs were adopted from an animal shelter. Assuming the truth of this assertion, find the probability that in a random sample of 80 pet dogs, between 15% and 20% were adopted from a shelter. You may assume that the normal distribution applies.
In one study it was found that 86% of all homes have a functional smoke detector. Suppose this proportion is valid for all homes. Find the probability that in a random sample of 600 homes, between 80% and 90% will have a functional smoke detector. You may assume that the normal distribution applies.
A state insurance commission estimates that 13% of all motorists in its state are uninsured. Suppose this proportion is valid. Find the probability that in a random sample of 50 motorists, at least 5 will be uninsured. You may assume that the normal distribution applies.
An outside financial auditor has observed that about 4% of all documents he examines contain an error of some sort. Assuming this proportion to be accurate, find the probability that a random sample of 700 documents will contain at least 30 with some sort of error. You may assume that the normal distribution applies.
Suppose 7% of all households have no home telephone but depend completely on cell phones. Find the probability that in a random sample of 450 households, between 25 and 35 will have no home telephone. You may assume that the normal distribution applies.
Some countries allow individual packages of prepackaged goods to weigh less than what is stated on the package, subject to certain conditions, such as the average of all packages being the stated weight or greater. Suppose that one requirement is that at most 4% of all packages marked 500 grams can weigh less than 490 grams. Assuming that a product actually meets this requirement, find the probability that in a random sample of 150 such packages the proportion weighing less than 490 grams is at least 3%. You may assume that the normal distribution applies.
An economist wishes to investigate whether people are keeping cars longer now than in the past. He knows that five years ago, 38% of all passenger vehicles in operation were at least ten years old. He commissions a study in which 325 automobiles are randomly sampled. Of them, 132 are ten years old or older.
A state public health department wishes to investigate the effectiveness of a campaign against smoking. Historically 22% of all adults in the state regularly smoked cigars or cigarettes. In a survey commissioned by the public health department, 279 of 1,500 randomly selected adults stated that they smoke regularly.
In an effort to reduce the population of unwanted cats and dogs, a group of veterinarians set up a low-cost spay/neuter clinic. At the inception of the clinic a survey of pet owners indicated that 78% of all pet dogs and cats in the community were spayed or neutered. After the low-cost clinic had been in operation for three years, that figure had risen to 86%.
An ordinary die is “fair” or “balanced” if each face has an equal chance of landing on top when the die is rolled. Thus the proportion of times a three is observed in a large number of tosses is expected to be close to 1/6 or Suppose a die is rolled 240 times and shows three on top 36 times, for a sample proportion of 0.15.
,
,
, yes
and
and
0.9977
0.3483
0.7357